4.5. Взаимно-корреляционная функция и взаимный энергетический спектр двух случайных процессов

Связь между двумя стационарными процессами х(t) и y(t) оценивается с помощью взаимно-корреляционной функции, определяемой выражениями^*

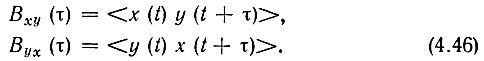
^* (Подразумевается, что не только сами процессы x(t) и y(t), но и связи между ними стационарны.)

В данном параграфе рассматриваются эргодические процессы поэтому вместо (4.46) можно применять временное усреднение

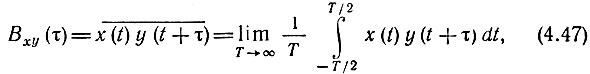
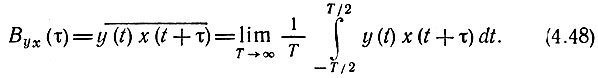
Как и для детерминированных колебаний, взаимно-корреляционная функция не изменяется, если сдвиг на τ одной из функций х(t) или y(t) заменить на сдвиг в обратном направлении другой функции. Поэтому можно написать следующие равенства:

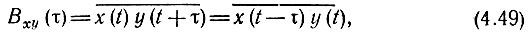
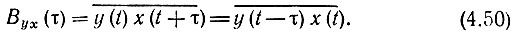
Из последних выражений вытекают следующие соотношения между В_xy(τ) и В_yx(τ):

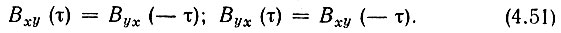
Соотношения (4.49)-(4.51) не следует смешивать с условиями четности функций. Каждая из функций В_xy(τ) и В_yx(τ) не обязательна четна относительно τ (см. § 2.16).

В итоге корреляция между значениями функций х(t) и y(t) в два различных момента времени, разделенных интервалом τ, задается корреляционной матрицей

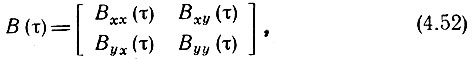
где В_хх(τ) и В_уу(τ) - корреляционные функции соответственно процессов х(t) и y(t).

Пусть, например, рассматривается сумма двух эргодических процессов х(t) и y(t) с нулевыми средними и требуется определить корреляционную функцию случайного процесса s(t) = х (t) + y(t) (при условии, что взаимно-корреляционные функции стационарны).

Используя формулу (4.16) и учитывая равенства (4.49), (4.50), получаем

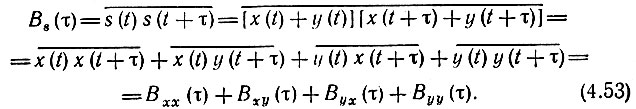
При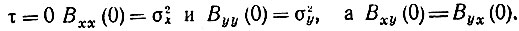

Следовательно,

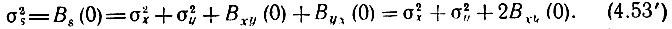
Если процессы х(t) и y(t) независимы, то дисперсия (средняя мощность) суммы будет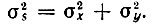

В противном случае в зависимости от знака В_xy(0) мощность процесса s(t) может быть больше или меньше суммы дисперсий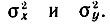

Для разности s(t) = х(t) - y(t) получается выражение, аналогичное (4.53'). Необходимо лишь знак плюс перед членом 2В_ху заменить минусом.

При независимости процессов x(t)и y(t) дисперсия процесса s(t), как при суммировании, будет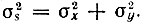

В практике часто встречается случай суммирования процесса x(t) с процессом Кх(t - T), т. е. с тем же процессом, задержанным на время Т и усиленным в К раз (рис. 4.12).

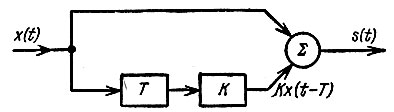
Рис. 4.12. К определению корреляционной функции суммы двух случайных процессов с одинаковыми энергетическими спектрами

Составим матрицу (4.52) для процессов 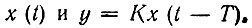В обозначениях (4.52) получаем

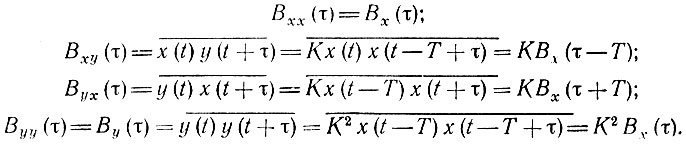
Таким образом, корреляционная матрица процессов х(t) и y(t) = Кх(t - Т) принимает вид

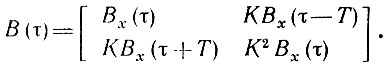
Найдем теперь корреляционную функцию процесса s(t) = x(t) + y(t) на выходе сумматора (рис. 4.12). Подставив в (4.53) элементы матрицы В(τ), получим

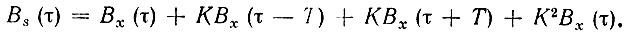
Приравнивая τ = 0, находим дисперсию процесса

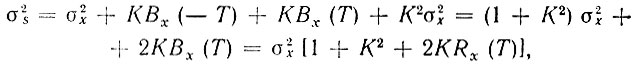
где 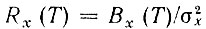- нормированная корреляционная функция процесса х(t) (напомним, что в данном примере положено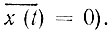

При замене сумматора вычитающим устройством знак плюс перед слагаемым 2KR_x(Т) должен быть заменен минусом.

Если задержка Т значительно больше интервала корреляции процесса х(t), то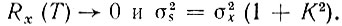

Применим теперь к B_s(τ) соотношение Винера-Хинчина (4.38):

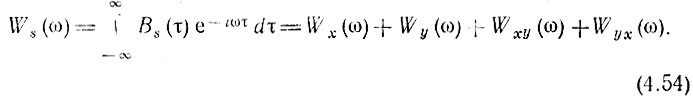
В этом выражении

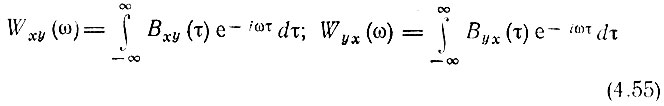
имеют смысл взаимных энергетических спектров случайных процессов х(t) и y(t).

Обратные преобразования Фурье, примененные к W_xy(ω) и W_yx(ω), принимают вид

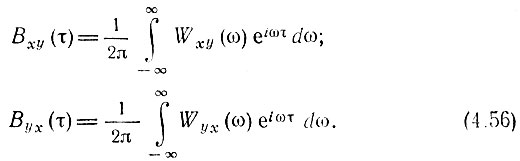
В отличие от энергетического спектра W_x(ω) или W_y(ω), являющегося действительной функцией ω и не могущего принимать отрицательные значения, взаимные спектральные плотности W_xy(ω) и W_yx(ω) могут быть комплексными функциями. Это имеет место при нечетных относительно τ функциях В_хy(τ) и В_yх(τ), Подстановка в (4.55) соотношения (4.51) приводит к равенству

откуда следует, что

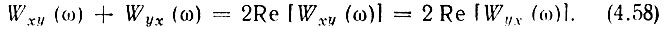
Таким образом, выражение (4.54) можно записать в форме

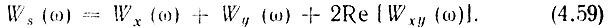
Это выражение поясняет физический смысл взаимного энергетического спектра W_xy(ω). Если случайные процессы х(t) и y(t) статистически независимы, то W_xy(ω) = 0 и энергетический спектр суммы s(t) = х(t) + y(t) равен сумме энергетических спектров W_x(ω) и W_y(ω) и, следовательно, мощность процесса s(t) равна сумме мощностей процессов х(t) и y(t).

Если действительная часть взаимного энергетического спектра положительна, то W_s(ω) > W_x(ω) + W_y(ω) и, следовательно, корреляция между процессами приводит к возрастанию средней мощности суммы 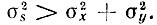Очевидно, что при отрицательной действительной части W_xy(ω) мощность суммарного процесса меньше, чем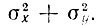

Если 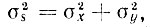то процессы х(t) и y(t) являются некогерентными, аддитивными (см. § 2.18).