4.4. Соотношение между энергетическим спектром и корреляционной функцией случайного процесса

Чем медленнее изменяется во времени х(t), тем уже энергетический спектр. С другой стороны, скорость изменения х(t) определяет ход корреляционной функции. Очевидно, что между W_x(ω) и В_х(τ) имеется тесная связь.

Существует теорема Винера-Хинчина, утверждающая, что В_х(τ) и W_x(τ) связаны между собой преобразованиями Фурье:

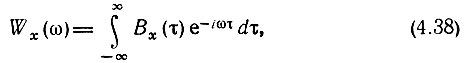
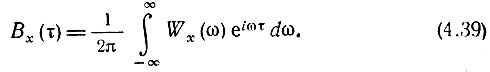
Из этих выражений вытекает свойство, аналогичное свойствам преобразований Фурье, установленным в гл. 2 для детерминированных сигналов: чем шире энергетический спектр случайного процесса, тем меньше интервал корреляции, и, соответственно, чем больше интервал корреляции, тем уже спектр процесса.

Большой интерес представляет белый шум, когда энергетический спектр равномерен на всех частотах - ∞ < ω < ∞.

Если в выражение (4.39) подставить W_x(ω) = W₀ = const, то получим [см. (2.93)]

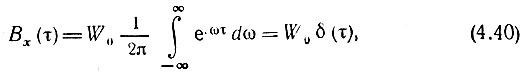
где δ(τ) - дельта-функция.

Для белого шума с бесконечным и равномерным спектром корреляционная функция равна нулю для всех значений τ, кроме τ = 0, при котором В_х(0) обращается в бесконечность. Подобный шум, имеющий игольчатую структуру с бесконечно тонкими случайными выбросами, иногда называют дельта-коррелированным процессом. Дисперсия белого шума бесконечно велика.

Поясним применение приведенных выше соотношений на примерах.

1. Пусть заданы следующие параметры напряжения шума (нормальный стационарный процесс с нулевым средним): среднеквадратическое значение u_ск = 2 В, энергетический спектр W₁(ω) равномерен в полосе частот от 0 до f₁ = 10 МГц (сплошная линия на рис. 4.9).

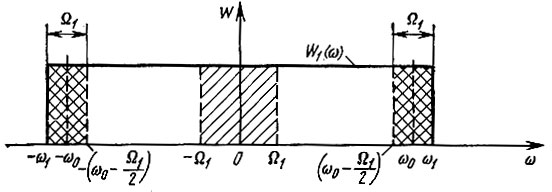
Рис. 4.9. Широкополосный и узкополосный энергетический спектры (примеры 1, 2, 3)

Шум с подобным спектром обычно называют широкополосным. В данном случае

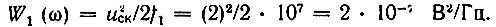
Корреляционная функция рассматриваемого процесса [см. (4.39)]

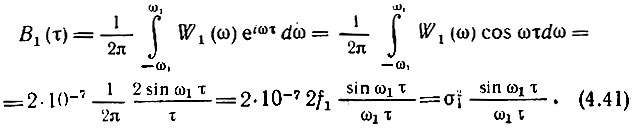
Дисперсия шума

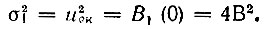
Нормированная корреляционная функция (рис. 4.10, а)

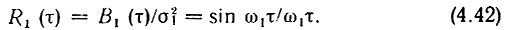
2. Вырежем из спектра исходного шума полосу от ω = -Ω₁ = -2πF₁ до ω = Ω₁ = 2πF₁ обозначенную на рис. 4.9 штриховкой, и найдем В₂(τ), R₂(τ) и σ₂², соответствующие этому шуму.

При F₁ = 2 МГц получим

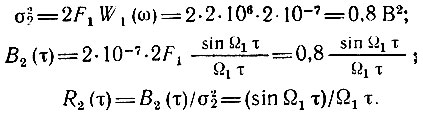
Сужение спектра привело к растяжению графика R₂(τ) по оси τ (рис. 4.10, а). Интервал корреляции увеличился в f₁/F₁ = 5 раз.

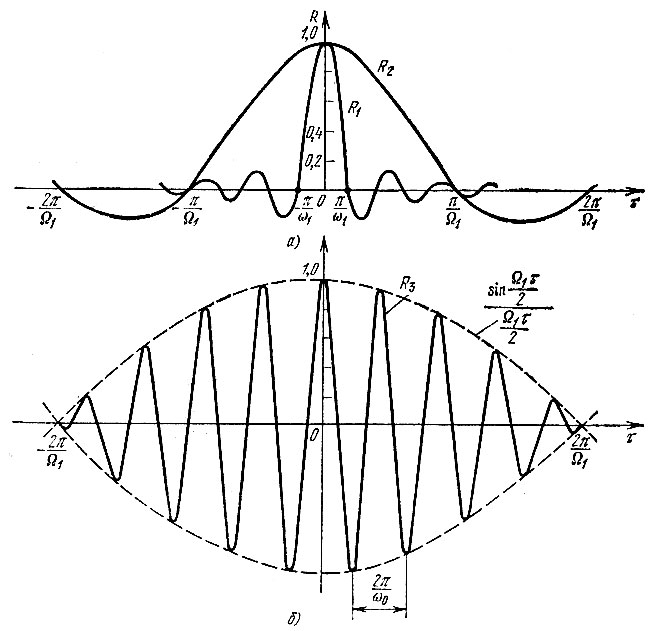
Рис. 4.10. Нормированная корреляционная функция случайного процесса с энергетическим спектром, равномерным в полосе:

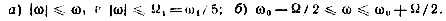
3. Найдем аналогичные характеристики для шума, спектр которого обозначен на рис. 4.9 двойной штриховкой. От предыдущего этот случай отличается положением спектральной полосы на оси частот. Шум с подобным спектром называют узкополосным (при Ω₁/ω₀ << 1).

Дисперсия этого шума σ₃², очевидно, не отличается от σ₂².

Корреляционная функция

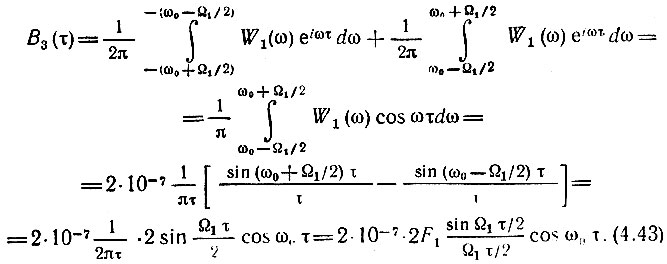
Нормированная корреляционная функция (рис. 4.10, б)

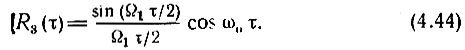
Огибающая функции R₃(τ) (штриховая линия) совпадает по форме с функцией R₂(τ), однако эта функция имеет вдвое большую протяженность. Высокочастотное заполнение функции R₃(τ) имеет частоту ω₀, равную центральной частоте спектра шума (см. рис. 4.9).

График нормированной корреляционной функции, показанный на рис. 4.10, б, позволяет составить представление о характере шумового колебания с узкополосным спектром. Осцилляции корреляционной функции с частотой ω₀ указывают на то, что и мгновенное значение шумового колебания изменяется в среднем с частотой ω₀. Напомним, что корреляционная функция гармонического колебания является также гармонической функцией той же частоты (см. § 2.16). Изменение же огибающей корреляционной функции по закону 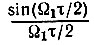указывает на то, что огибающая шумового колебания, являющаяся случайной величиной, изменяется во времени относительно медленно, подобно функции времени, спектр которой ограничен наивысшей частотой Ω₁. Примерный вид шумового колебания, соответствующего корреляционной функции (4.44), представлен на рис. 4.11 (в измененном масштабе времени по оси абсцисс).

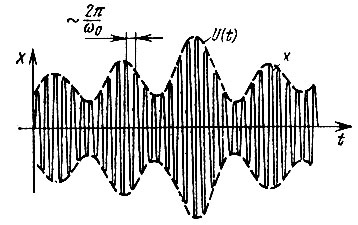
Рис. 4.11. Примерный вид реализации случайного процесса, корреляционная функция которого показана на рис. 4.10, б (масштабы по осям t и τ разные)

Итак, шумовое колебание с узкополосным спектром следует представлять себе как высокочастотное колебание с медленно (по сравнению с частотой ω₀) изменяющимися амплитудой и фазой:

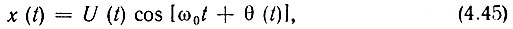
где ω₀ - центральная частота спектра шума.

Следует подчеркнуть, что все параметры этого колебания: амплитуда, фаза и частота - являются случайными функциями времени. Статистические характеристики этих параметров рассматриваются в § 4.6.