5.2. Определения и основные свойства активной цепи

В общей теории цепей под активной подразумевается цепь, содержащая наряду с пассивными элементами (катушками индуктивности, конденсаторами и резисторами) также и источники энергии (генераторы э. д. с. или генераторы тока).

Активный характер цепей радиоэлектронных устройств обусловлен применением в них усилительных элементов: транзисторов, электронных ламп, ламп бегущей волны и т. д. При этом предполагается, что энергия сигнала на выходе активной цепи больше, чем на входе. Для большей определенности видоизменим формулировку следующим образом: цепь активна, если при гармоническом возбуждении средняя мощность сигнала на выходе больше мощности на входе, т. е. коэффициент усиления по мощности больше единицы. Из такого определения ясно, что цепь, осуществляющая усиление напряжения, например, с помощью повышающего трансформатора без усиления мощности является пассивной, даже если в нее входят активные элементы со своими источниками питания.

При построении схем замещения активных цепей источники постоянного тока или напряжения опускаются. На этих схемах активные элементы (транзисторы, лампы и др.) отображаются с помощью эквивалентных параметров, которые зависят от режима работы активного элемента и в конечном счете от источников энергии, питающих активный элемент. При этих допущениях любой (как активный, так и пассивный) линейный четырехполюсник можно представить схемой, изображенной на рис. 5.1 На этом рисунке Е₁, Е₂, Ι₁ и Ι₂ обозначают комплексные амплитуды гармонических напряжений и токов независимых источников при фиксированной частоте ω.

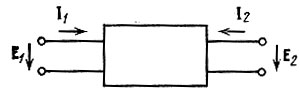
Рис. 5.1. Схема замещения линейного четырехполюсника

Четырехполюсник полностью характеризуется соотношениями между напряжениями и токами на его входе и выходе. Вид этих соотношений зависит от выбора исходных величин.

Напомним вкратце основные формы представления четырехполюсников.

Если исходными являются напряжения Е₁ и Е₂, то уравнения для определения токов Ι₁ и Ι₂ записываются в форме

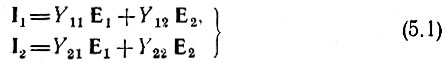
или в матричной форме

где

является матрицей параметров, имеющих смысл и размерность проводимостей.

Если уравнение (5.1) решить относительно Е₁ и Е₂ то получатся системы уравнений

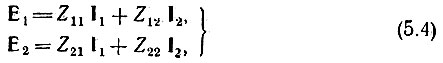
где

является матрицей параметров, имеющих размерность сопротивлений.

Исходным уравнениям четырехполюсника, записанным в форме

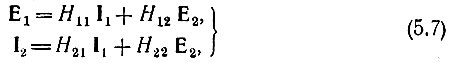
соответствует матрица параметров

в которой H₁₁ имеет размерность сопротивления, H₂₂ - проводимости, а H₁₂ и H₂₁ - безразмерные параметры.

Приведем еще уравнения в форме

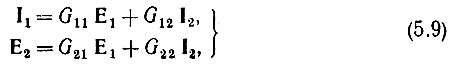
которой соответствует матрица

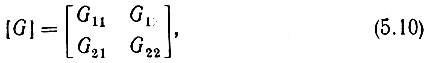
где G₁₁ - проводимость; G₂₂ - сопротивление, а G₁₂ и G₂₁ - безразмерные параметры.

В теории усилителей наибольшее распространение получили матрицы Z-, Y- и H-параметров. Связь между одними и теми же величинами, выраженными через различные системы параметров, представлена в табл. 5.1. В этой таблице определители ΔY, ΔZ и ΔH соответствующих матриц определяются выражениями

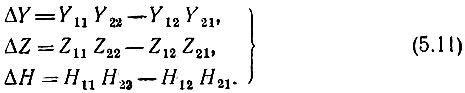
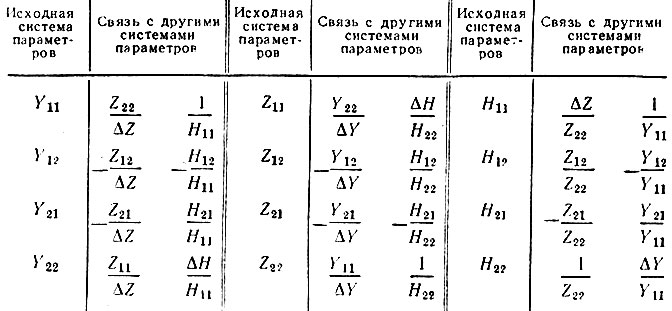
Таблица 5.1

Уравнения (5.1), (5,4), (5.7) и аналогичные им другие уравнения позволяют построить эквивалентные схемы замещения четырехполюсников.

На рис. 5.2, а изображена схема замещения^*, построенная в соответствии с уравнением (5.1). На этой схеме оба напряжения Ε₁ и Ε₂ рассматриваются как напряжения от внешних источников. Генератор тока Υ₁₂Ε₂ учитывает влияние напряжения Ε₂ на входной ток Ι₁, а генератор тока Υ₂₁Ε₁ - влияние входного напряжения Ε₁ на величину тока Ι₂. Оба генератора можно рассматривать как "зависимые источники", так как обеспечиваемые ими токи пропорциональны напряжениям внешних источников. Параметр Υ₂₁ имеет смысл взаимной проводимости от входа к выходу, а Υ₁₂ - от выхода к выходу. Очевидно также, что Υ₁₁ есть входная проводимость четырехполюсника при Ε₂ = 0, т. е. при коротком замыкании выхода, а Υ₂₂ - входная проводимость при возбуждении четырехполюсника от источника Ε₂ при коротком замыкании входа.

^* (Наличие общей шины на рис. 5.2 и последующих аналогичных схемах позволяет говорить о трехполюснике. Это не оказывает влияния на уравнение цепи.)

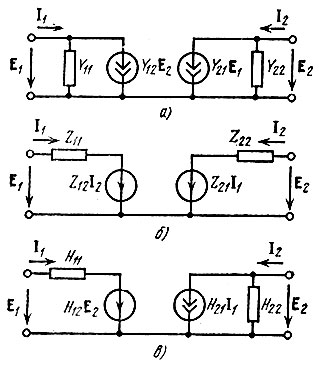
Рис. 5.2. Схемы замещения четырехполюсника, основанные на матрице: а) Y-параметров; б) Z-параметров; в) H-параметров

Эквивалентная схема четырехполюсника, соответствующая уравнениям (5.4) и (5.5), изображена на рис. 5.2, б. На этой схеме зависимые источники напряжения Ζ₁₂Ι₂ и Ζ₂₁Ι₁ учитывают влияние Ι₂ на Ε₁ и Ι₁ на Ε₂ соответственно. Уравнениям (5.7), (5.8) соответствует схема замещения, показанная на рис. 5.2, в.

Здесь необходимо отметить следующую особенность активного четырехполюсника: как правило, Υ₂₁ ≠ Υ₁₂ или Ζ₂₁ ≠ Ζ₁₂, Н₂₁ ≠ H₁₂. Это означает, что активные четырехполюсники необратимы и, следовательно, принцип взаимности к активным четырехполюсникам неприменим.

Взаимные проводимости или сопротивления пассивных четырехполюсников, как известно, равны (теорема взаимности). Это позволяет схемы замещения, показанные, например, на рис. 5.2, а и б, упростить для пассивного четырехполюсника и привести их к виду, при котором зависимые источники отсутствуют (рис. 5.3).

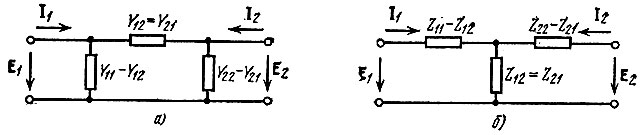
Рис. 5.3. Преобразование схем замещения, изображенных на рис. 5.2, а и б, справедливое только для пассивного четырехполюсника

При анализе радиотехнических цепей особенно часто приходится иметь дело с четырехполюсниками, возбуждаемыми только со стороны входа; под выходным напряжением при этом подразумевается падение напряжения на сопротивлении нагрузки Z_H = 1/G_H, т. е. Ε₂ = -Ι₂Z_H. В подобных случаях нагрузочный элемент целесообразно вводить внутрь четырехполюсника.

При представлении четырехполюсника с помощью Υ-матрицы получается схема замещения, показанная на рис. 5.4, а, которая отличается от схемы на рис. 5.2, а только тем, что нагрузочная проводимость G_H добавлена к Υ₂₂. Это позволяет рассматривать новый четырехполюсник как разомкнутый, у которого ток на выходе Ι'₂ = 0. Матрица параметров этого нового четырехполюсника

где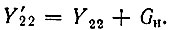

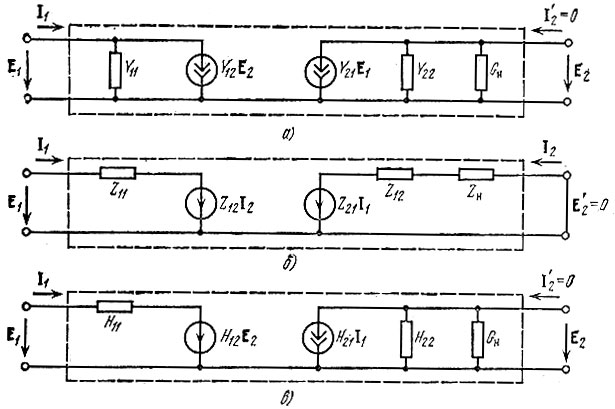
Рис. 5.4. Введение нагрузочного элемента в состав четырехполюсника

Второе уравнение (5.1) принимает при этом вид

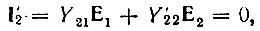
откуда следует важное соотношение

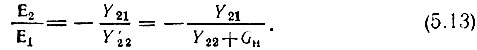
Исключив с помощью этого соотношения Ε₁ из первого уравнения (5.1), а также учитывая, что 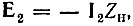получим отношение токов

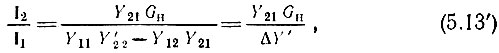
где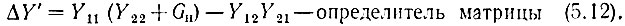

При использовании Z-матрицы схема замещения принимает вид, показанный на рис. 5.4, б. В данном случае выходные зажимы замкнуты накоротко (Ε'₂ = 0), а матрица параметров

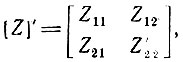
где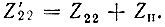

Второе уравнение (5.4) при этом приводит к соотношению

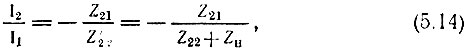
а первое уравнение к соотношению

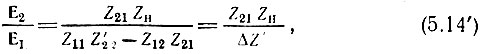
где 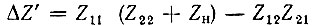- определитель матрицы [Z]'.

Наконец, второе уравнение (5,7) при подстановке Н'₂₂ = Н₂₂ + G_H и Ε₂ = - Ι₂Ζ_H (рис. 5.4, в) дает

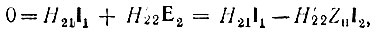
откуда следует соотношение

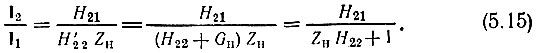
Исключив с помощью этого соотношения Ι₁ из первого уравнения (5.7), получим

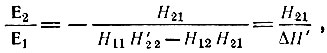
где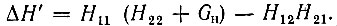

Общие уравнения (5.1), (5.4) и (5.7) можно преобразовать таким образом, что соответствующие им схемы замещения четырехполюсника будут содержать только по одному зависимому источнику.

Так, например, записав второе уравнение (5.1) в форме

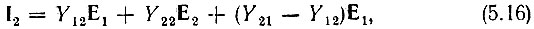
приходим к схеме замещения (рис. 5.5, а), содержащей один зависимый источник тока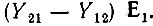

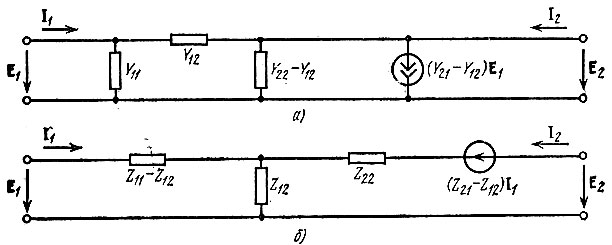
Рис. 5.5. Схемы замещения с одним зависимым источником тока (а) или напряжения (б)

Аналогично записав второе уравнение (5.4) в форме

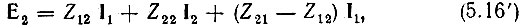
приходим к схеме с одним зависимым источником напряжения (Z₂₁ - Z₁₂) Ι₁ (рис. 5.5, б).