
5.3. Активный четырехполюсник как линейный усилитель
Приведенные в предыдущем параграфе выражения (5.13)-(5.16), записанные в форме
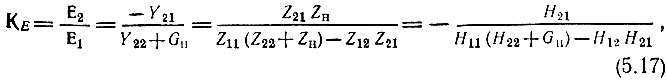
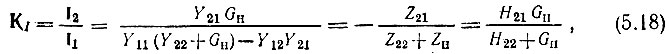
можно рассматривать как коэффициенты усиления соответственно по напряжению и по току в активном четырехполюснике.
В широкополосных усилителях, как правило, усилительные приборы (транзисторы, лампы и др.) обеспечивают (при правильном выборе нагрузки) выполнение следующих неравенств:

Поэтому при грубой оценке усилительной способности четырехполюсника можно исходить из приближенных равенств


Отсюда следует, что коэффициент усиления по мощности (выраженной в вольтамперах)
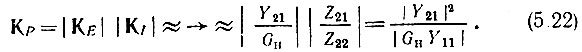
(Здесь использованы соотношения между Z21-, Z22- и Y-параметрами из табл. 5.1.)
Из (5.22) очевидна решающая роль параметра Y21 (соответственно Z21 и H21) в усилении мощности колебания в активном четырехполюснике. Физический смысл этого параметра раскрывается в следующих параграфах на примерах некоторых усилительных приборов.
При анализе активного четырехполюсника как усилителя важное значение имеют такие его параметры, как входное и выходное сопротивления. На рис. 5.6 представлена обобщенная схема, содержащая источник сигнала Ес, активный четырехполюсник и сопротивление нагрузки ZH.
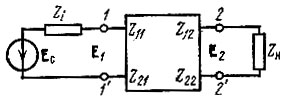
Рис. 5.6. Обобщенная схема активного четырехполюсника с учетом параметров источника сигнала и нагрузки
Входное сопротивление (между зажимами 1-1') легко определить с помощью уравнений (5.4) в сочетании с (5.14).
Подставив Ι2 из (5.14) в первое уравнение (5.4), получим
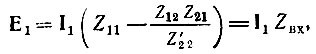
откуда
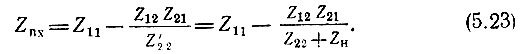
Под выходным сопротивлением четырехполюсника подразумевается сопротивление между зажимами 2-2' при Εc = 0 (но с учетом внутреннего сопротивления источника сигнала Zi). Сопротивление Zi рассматривается при этом как нагрузка.
По аналогии с (5.23) при замене Z11 на Z22 и ZH на Zi получаем
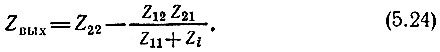
При учете внутреннего сопротивления Zi источника сигнала под коэффициентом усиления следует подразумевать отношение Ε2/Εc = ΚE. Этот коэффициент можно найти с помощью соответствующих формул (5.17), (5.18) добавлением Zi к Z11 или Н11. Таким образом,
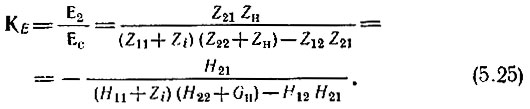
При использовании Y-матрицы нетрудно получить выражение
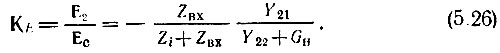
Это выражение совпадает с обычным определением передаточной функции линейного четырехполюсника.
Из приведенных общих соотношений видно, что структура передаточной функции активного четырехполюсника и характер частотной зависимости этой функции определяются частотными свойствами параметров Z или Y. В этом отношении между линейными активным и пассивным четырехполюсниками нет никакого различия. Задание Z(ω) и Y(ω) однозначно определяет и временные характеристики линейной активной цепи: импульсную характеристику и переходную функцию.
Определяемая формулами (5.17), (5.18) безразмерная, в общем случае комплексная функция является важнейшей характеристикой четырехполюсника. Она определяется в стационарном режиме при гармоническом возбуждении четырехполюсника.
Передаточную функцию часто удобно представлять в форме

Модуль К(ω) иногда называют амплитудно-частотной или просто частотной характеристикой четырехполюсника. Аргумент φ(ω) коэффициента передачи называют фазочастотной (или просто фазовой) характеристикой четырехполюсника.
Для активных линейных цепей, как и для пассивных, под импульсной характеристикой цепи g(t) подразумевается отклик, реакция цепи на воздействие, имеющее вид единичного импульса (дельта-функции). Связь между g(t) и К(iω) нетрудно установить с помощью интеграла Фурье.
Если на входе четырехполюсника действует единичный импульс э. д. с., обладающий спектральной плотностью, равной единице для всех частот, то спектральная плотность выходного напряжения равна просто К(iω). Следовательно, отклик на единичный импульс, т. е. импульсная характеристика цепи, легко определяется с помощью обратного преобразования Фурье [см. (2.49)], примененного к передаточной функции К(ω):
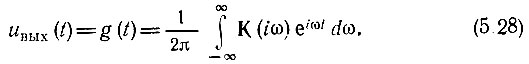
В дальнейшем импульсную характеристику будем обозначать функцией g(t), под которой можно подразумевать не только напряжение, но и любую другую электрическую величину, являющуюся откликом на воздействие в виде дельта-функции.
Если передаточная функция задана в виде функции Κ(р), т. е. в виде преобразования Лапласа от функции g(t), то выражение (5.28) можно записать* в форме обратного преобразования Лапласа
* (Здесь и в дальнейшем обозначения передаточной функции цепи, рассматриваемой как преобразование Фурье или Лапласа от импульсной характеристики g(t), будут различаться только аргументом: К(iω) или К(р) (см. § 2.13).)
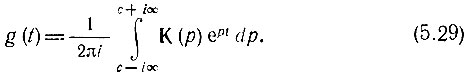
Переходная функция цепи h(t) представляет собой отклик, реакцию цепи на воздействие, имеющее вид "единичного скачка". Так как такое воздействие является интегралом от единичного импульса (т. е. дельта-функции), то и между h(t) и g(t) существует интегральное соотношение

В последующих главах при анализе передачи сигналов через радиоцепи чаще всего будет применяться импульсная характеристика g(t).

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
