8.6. Амплитудное ограничение

В радиотехнике часто возникает необходимость устранить нежелательные изменения амплитуды высокочастотного колебания, возникающие из-за накладки помех на радиосигнал, при передаче частотно-модулированных колебаний через избирательные цепи и т. д.

Для этого широко используются амплитудные ограничители, представляющие собой сочетание нелинейного элемента и избирательной нагрузки. Вольт-амперная характеристика нелинейного элемента должна иметь сильно выраженную горизонтальную часть, а полоса пропускания избирательной цепи должна быть не шире той, которая требуется для передачи информации, содержащейся в частоте (или фазе) ограничиваемого колебания. В качестве амплитудного ограничителя может быть использован, в частности, обычный нелинейный резонансный усилитель, рассмотренный в § 8.4, в режиме работы, показанном на рис. 8.18.

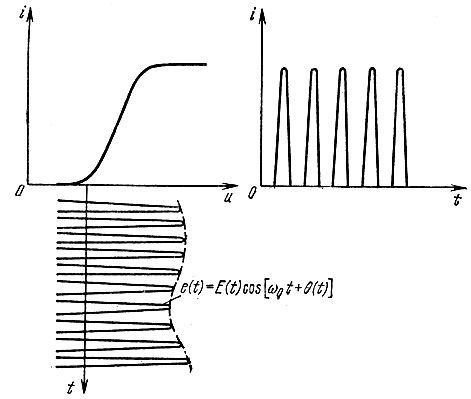
Рис. 8.18. Режим работы ограничителя амплитуды

Пусть к ограничителю подводится колебание вида

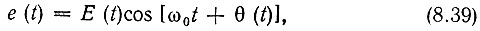
причем изменение огибающей Е(t) является нежелательным, паразитным фактором. Если это изменение не выходит за пределы горизонтального участка характеристики i = f(u), как это показано на рис. 8.18, то импульсы тока имеют одинаковую амплитуду, независимо от Е(t). Несколько изменяется лишь ширина вершины импульсов. Поэтому можно в первом приближении считать, что амплитуда первой гармоники, а следовательно, и амплитуда напряжения на колебательном контуре являются в некотором интервале изменения амплитуды Е(t) постоянными величинами.

Характеристику ограничителя с избирательной нагрузкой, обеспечивающей отфильтровывание высших гармоник, можно представить в виде, изображенном на рис. 8.19. Через E_пор обозначено пороговое значение амплитуды входного напряжения, начиная с которого обеспечивается полное ограничение на уровне U₀.

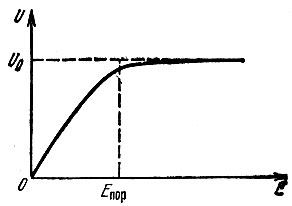
Рис. 8.19. Характеристика резонансного ограничителя

При Е(t) > Е_пор амплитуда на выходе почти не изменяется. Фаза же первой гармоники тока и соответственно выходного напряжения совпадает с фазой напряжения на входе ограничителя.

Поэтому для выходного напряжения можно написать следующее выражение:

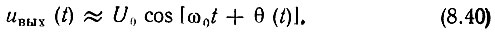
Амплитуда выходного напряжения U₀ определяется параметрами нелинейного элемента и избирательной нагрузки. Для схемы, изображенной на рис. 8.15, б, U₀ = I₁Z_эp, где I₁ - амплитуда первой гармоники, определяемая с учетом уплощения вершины импульса, а Z_эp - эквивалентное резонансное сопротивление контура.

Для ряда практических задач особый интерес представляет воздействие на амплитудный ограничитель двух сигналов с близкими частотами.

Пусть, например, определяемое выражением (8.39) напряжение е(t) является суммой двух гармонических колебаний:

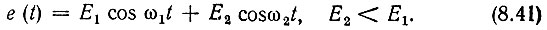
Каждое из этих напряжений, действуя отдельно, создает на выходе ограничителя простое гармоническое колебание с частотой ω₁ (или ω₂) и с амплитудой U₀. Иная картина получается при одновременном воздействии на ограничитель двух гармонических напряжений. Для определения напряжения на выходе ограничителя входное колебание необходимо привести к виду выражения (8.39).

Для этого обозначим через Ω разность частот 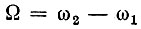и сделаем в (8.41) следующую подстановку:

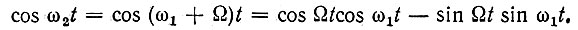
Тогда

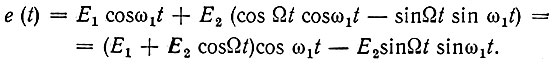
Рассматривая множители при cos ω₁t и sin ω₁t как медленно меняющиеся функции времени (поскольку Ω << ω₁), представим последнее выражение в несколько иной форме

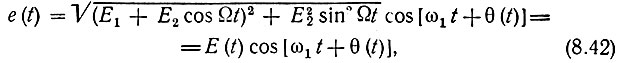
где огибающая результирующего напряжения Е(t) определяется выражением

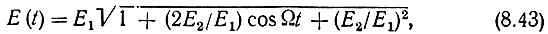
а фаза

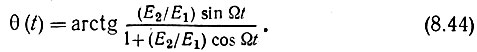
Огибающая E(t) имеет максимальное значение, равное Е₁ + Е₂ (при cos Ωt = 1), и минимальное, равное Е₁ - Е₂ (при cos Ωt = -1).

Допустим, что Е₁ - Е₂ > E_пор, так что условие ограничения выполняется для всех значений, которые может принимать амплитуда входного напряжения Е(t) (рис. 8.20). Тогда напряжение на выходе по аналогии с (8.40) можно записать в виде

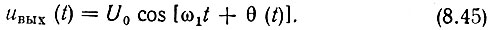
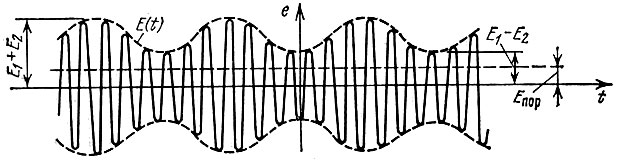
Рис. 8.20. Бигармоническое напряжение на входе амплитудного ограничителя

Получается фазомодулированное колебание, которое в отличие от входного напряжения е(t) может иметь широкий спектр.

Для определения амплитуд отдельных составляющих этого спектра можно воспользоваться теорией частотно-модулированных колебаний, изложенной в гл. 3.

Не приводя здесь подробного анализа, облегчим задачу, допустив, что Е₂ << Е₁. При этом выражение (8.44) упрощается:

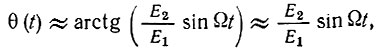
и напряжение на выходе^*

^* (Здесь мы не учитываем влияния неравномерности частотной характеристики контура в полосе частот, обусловленной фазовой модуляцией входного сигнала.)

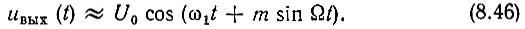
Здесь использовано обозначение

которое подчеркивает, что отношение амплитуд Е₂/Е₁ имеет в данном случае смысл индекса фазовой модуляции (см. § 3.4).

Выражение (8.46) полностью совпадает с (3.25) и по аналогии с (3.32) можно записать в форме

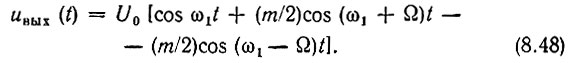
Спектр выходного напряжения при 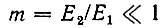состоит из трех составляющих с частотами ω₁, ω₁ + Ω = ω₂ и ω₁ - Ω = 2ω₁ - ω₂. Первые две частоты присутствуют на входе ограничителя, а третья (2ω₁ - ω₂) является продуктом взаимодействия входных колебаний в нелинейном элементе.

Соотношение спектров на входе и выходе ограничителя при Е₂/Е₁ << 1 показано на рис. 8.21. Частота 2ω₁ - ω₂ является "зеркальной" по отношению к частоте ω₂.

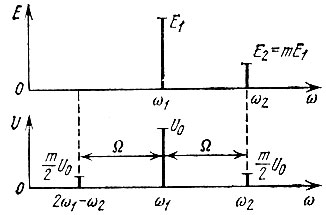
Рис. 8.21. Спектры колебаний на входе и выходе резонансного ограничителя при бигармоническом воздействии

Существенно, что амплитуда колебания с частотой ω₂ = ω₁ + Ω (а также с частотой ω₁ - Ω) составляет всего лишь m/2 от амплитуды колебания с частотой ω₁, в то время как на входе отношение амплитуд равно m. Это позволяет говорить о подавлении в ограничителе слабого колебания более сильным. Эффект подавления становится особенно наглядным, когда в полосу пропускания избирательной нагрузки попадают только частоты ω₁ и ω₂, а зеркальная частота ω₁ - Ω отфильтровывается^*. В этом случае спектральный состав напряжения на выходе такой же, как и на входе, только амплитуда слабого колебания по отношению к сильному уменьшается в два раза.

^* (Этот случай, правда, не характерен для ограничителя, так как отфильтрование зеркальной частоты приводит к непостоянству огибающей суммы двух напряжений.)

Если амплитуды двух колебаний на входе ограничителя соизмеримы, то эффект относительного подавления выражен слабее. Это видно из графика (рис. 8.22), построенного в предположении, что избирательная цепь ограничителя пропускает только компоненты с частотами ω₁ и ω₂, присутствующими на входе ограничителя [8].

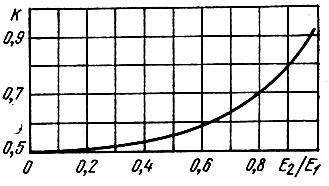
Рис. 8.22. Коэффициент подавления слабого колебания в амплитудном ограничителе при бигармоническом воздействии (Е₂ < Е₁)

По оси ординат отложен коэффициент подавления, представляющий собой отношение

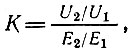
где Е₂/Е₁ - отношение амплитуд на входе, а U₂/U₁ на выходе ограничителя.

При 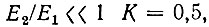а с приближением Е₂/Е₁ к единице К также приближается к единице. При Е₂/Е₁ = 1 оба колебания равноправны и взаимное подавление отсутствует.

В заключение следует отметить, что все приведенные выше рассуждения сохраняют свою силу и в случае, когда ω₂ < ω₁ необходимо лишь на рис. 8.21 поменять местами зеркальные частоты.