8.11. Синхронное детектирование

Рассмотрим особый вид преобразования, который получается при частоте гетеродина, равной частоте сигнала. Полагая в выражении (8.74) ω_s = ω_г и рассматривая сначала немодулированное входное колебание (Е_s = Е₀), получаем

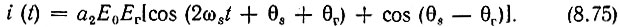
Как видим, в частном случае ω_г = ω_s колебание с нижней комбинационной частотой вырождается в постоянный ток

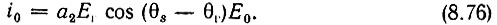
При θ_s - θ_г = 0 или π ток |i₀| достигает максимума, при θ_s - θ_г = π/2 ток i₀ = 0.

При включении на выходе преобразователя фильтра нижних частот колебание с частотой 2ω_s подавляется и на выходе фильтра остается одно лишь постоянное напряжение, пропорциональное току i₀.

При наличии амплитудной модуляции, когда e_s(t) = E_s(t) cos (ω_st + θ_s), колебание на выходе будет пропорционально току

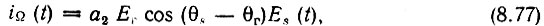
т. е. совпадать по форме с законом модуляции амплитуды высокочастотного колебания е_s(t).

Иными словами, на выходе преобразователя выделяется передаваемое сообщение, причем по отношению к входному колебанию, при Е_s(t) << E_р, обработка по существу является линейной.

Основным преимуществом такого способа обработки, предложенного в 1934 г. Е. Г. Момотом и называемого синхронным детектированием, является повышенная избирательность радиоприема слабых сигналов на фоне шума (устраняется взаимодействие сигнала с помехой в нелинейном устройстве, каковым является обычный амплитудный детектор).

Следует, однако, отметить, что реализация принципа синхронного детектирования связана со значительными трудностями, так как обеспечение синхронизма частоты гетеродина с частотой принимаемого сигнала является сложной задачей, особенно при приеме слабых сигналов на фоне помех.