8.10. Преобразование частоты сигнала

В радиотехнике часто требуется осуществить сдвиг спектра сигнала по оси частот на определенную постоянную величину при сохранении структуры сигнала. Такой сдвиг называется преобразованием частоты.

Для выяснения основных черт процесса преобразования частоты вернемся к вопросу о воздействии на нелинейный элемент двух напряжений, кратко рассмотренному в § 8.3. Однако в данном случае только одно из колебаний, именно то, которое создается вспомогательным генератором (гетеродином), мы будем считать гармоническим. Под вторым же колебанием будем подразумевать сигнал, подлежащий преобразованию, который может представлять собой любой сложный, но узкополосный процесс.

Таким образом, на нелинейный элемент воздействуют два напряжения:

- от гетеродина

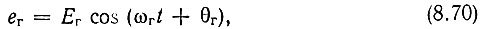
- от источника сигнала

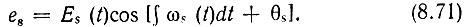
Амплитуда E_г, частота ω_г и начальная фаза θ_г гетеродинного колебания - постоянные величины. Амплитуда же Е_s(t) и мгновенная частота ω_s(t) сигнала могут быть модулированными, т. е. могут являться медленными функциями времени (узкополосный процесс). Начальная фаза сигнала θ_s - постоянная величина.

В качестве нелинейного элемента возьмем, как и в § 8.8, диод, однако характеристику его для более полного выявления продуктов взаимодействия сигнала и гетеродинного колебания аппроксимируем полиномом четвертой степени (а не второй, как в § 8.3):

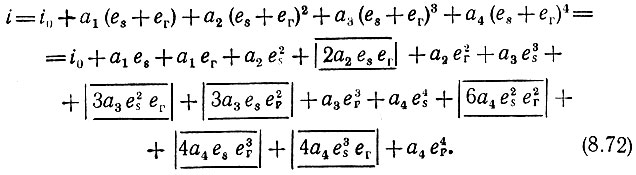
Слагаемые, содержащие различные степени только e_s или только е_г, интереса не представляют. С точки зрения преобразования (сдвига) частоты основное значение имеют члены, представляющие собой произведения вида e_sⁿe_г^m [в правой части выражения (8.72) обведены рамками]. Подставляя в эти произведения (8.70) и (8.71) и отбрасывая все составляющие, частоты которых не являются суммой ω_s + ω_г или разностью ω_s - ω_г, после несложных тригонометрических выкладок приходим к следующему окончательному результату:

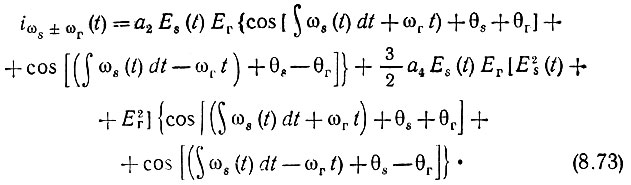
Из этого результата видно, что интересующие нас частоты ω_s ± ω_г возникают лишь благодаря четным степеням полинома, аппроксимирующего характеристику нелинейного элемента. Однако один лишь квадратичный член полинома (с коэффициентом а₂) образует составляющие, амплитуды которых пропорциональны только первой степени E_s(t). Более высокие четные степени (четвертая, шестая и т. д.) нарушают эту пропорциональность, так как амплитуды привносимых ими колебаний содержат также степени Е_s(t) выше первой.

Отсюда видно, что амплитуды Е_s и Е_г должны выбираться с таким расчетом, чтобы в разложении (8.72) преобладающее значение имели слагаемые не выше второй степени. Для этого требуется выполнение неравенств

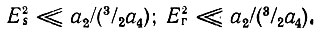
Тогда выражение (8.73) переходит в следующее:

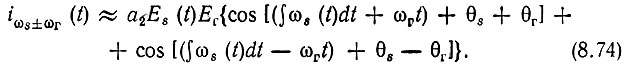
В радиоприемных и многих других устройствах, в которых задача преобразования частоты тесно связана с задачей усиления сигнала, обычно Е_s << Е_г.

Первое слагаемое в фигурных скобках с частотой ω_s(t) + ω_г (производная от аргумента косинуса) соответствует сдвигу спектра сигнала в область высоких частот, а второе с частотой ω_s(t) - ω_г - в область низких частот. Для выделения одной из этих частот - разностной или суммарной - нужно применять соответствующую нагрузку на выходе преобразователя. Пусть, например, частоты ω_s и ω_г очень близки и требуется выделить низкую частоту, расположенную около нуля. Такая задача часто встречается в Измерительной технике (метод "нулевых биений"). В этом случае нагрузка должна быть такой же, как при амплитудном детектировании, т. е. состоять из параллельного соединения R и С, обеспечивающего отфильтровывание (подавление) высоких частот ω_s и ω_г и выделение разностной частоты |ω_s - ω_г|. Если разностная частота |ω_s - ω_г| лежит в радиотехническом диапазоне, то для ее выделения следует применить резонансную колебательную цепь (рис. 8.42). Если полезной, подлежащей выделению, является суммарная частота ω_s + ω_г, то контур соответственно должен быть настроен на частоту ω_p = ω_s + ω_г.

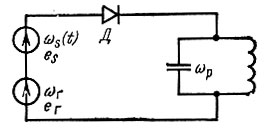
Рис. 8.42. Схема замещения преобразователя частоты

Обычно полоса пропускания колебательной цепи, являющейся нагрузкой преобразователя, рассчитана на ширину спектра модулированного колебания. При этом все составляющие тока с частотами, близкими к 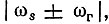проходят через контур равномерно и структура сигнала на выходе совпадает со структурой сигнала на входе. Единственное отличие заключается в том, что частота на выходе равна (ω_s(t) + ω_г или ω_s(t) - ω_г, смотря по тому, какова резонансная частота нагрузочной цепи.

Итак, при преобразовании частоты законы изменения амплитуды E_s(t), частоты ω_s(t) и фазы ∫ω_s(t)dt входного колебания переносятся на выходное колебание. В этом смысле рассматриваемое преобразование сигнала является линейным, а устройство - линейным преобразователем или "смесителем".

В заключение следует отметить, что при использовании разностной частоты полное сохранение структуры сигнала получается лишь в том случае, когда ω_s(t) > ω_г. Если же ω_s(t) < ω_г, то имеет место "переворачивание" спектра сигнала.

На рис. 8.43, а изображена спектральная диаграмма сигнала на входе и выходе преобразователя для случая, когда все частоты, входящие в спектр входного колебания, выше частоты гетеродина ω_г. Преобразованный спектр, сдвинутый на величину ω_г влево, имеет такую же структуру, что и исходный спектр. Случай ω_г > ω_s(t) изображен на рис. 8.43, б. В преобразованном спектре ω_макс и ω_мин меняются местами.

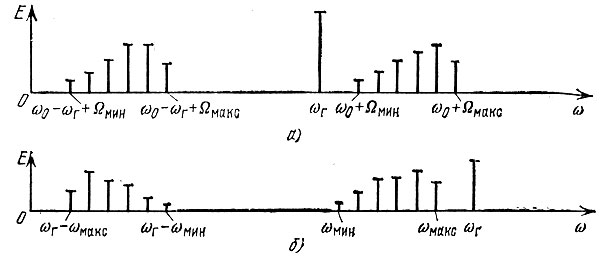
Рис. 8.43. Спектр сигнала на входе и выходе преобразователя: а - при ω_s > ω_г; б - при ω_s < ω_г

При преобразовании частоты обычного амплитудно-модулированного колебания, состоящего из двух симметричных относительно ω₀ боковых полос, переворачивание спектра внешне никак не проявляется; просто верхняя и нижняя боковые полосы меняются местами. При преобразовании же частотно-модулированного колебания мгновенная частота которого ω_s(t) = ω₀ + Δω(t), случай ω_г > ω_s(t) приводит к изменению мгновенной частоты выходного сигнала по закону

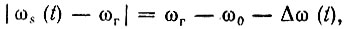
т. е. к изменению знака перед частотным отклонением Δω(t).

Из приведенных примеров ясно, что с переворачиванием спектра при преобразовании частоты необходимо считаться только в тех случаях, когда спектр сигнала несимметричен относительно своей центральной частоты (при частотной модуляции асимметрия заключается в том, что знаки перед нижними боковыми частотами ω₀ - nΩ при нечетных n отрицательны, см. § 4.6).

При преобразовании частоты сигнала с несимметричным спектром для сохранения структуры спектра частота гетеродина должна быть ниже частот сигнала.