8.9. Частотное и фазовое детектирование

Напряжение на выходе частотного детектора должно воспроизводить закон изменения мгновенной частоты модулированного колебания. Представив последнее в форме

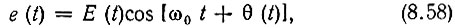
получим для идеального частотного детектора следующую функциональную связь:

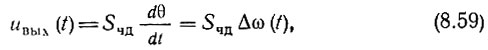
где S_чд = const - крутизна характеристики детектора, выраженная в вольтах на единицу угловой частоты; Δω(t) = dθ/dt - мгновенное значение частотного отклонения входной э. д. с. Если пользоваться частотами f = ω/2π, то в выражении

крутизна характеристики S_чд будет иметь размерность В/Гц.

Предполагается, что Δf(t), а следовательно, и u_вых(t) являются "медленными" функциями времени. Для выделения сообщения из частотно-модулированного колебания, спектр которого состоит только из высокочастотных составляющих (несущая частота и боковые частоты модуляции), необходимо нелинейное устройство. Следовательно, частотный детектор обязательно должен включать в себя нелинейный элемент. Однако в этом случае в отличие от амплитудного детектора для образования частот сообщения одного лишь нелинейного элемента недостаточно. Действительно, из вольт-амперных характеристик нелинейных элементов видно, что при постоянстве амплитуды входного напряжения нелинейный элемент не реагирует на изменение частоты этого напряжения. Иными словами, нелинейность таких устройств, как диод, проявляется лишь при изменении величины действующего на них напряжения, а не при изменении частоты или в общем случае скорости изменения сигнала. Поэтому обычный частотный детектор представляет собой сочетание двух основных частей: 1) избирательной линейной цепи, преобразующей частотную модуляцию в амплитудную и 2) амплитудного детектора.

При правильном построении схемы частотного детектора изменение амплитуды входного сигнала не должно влиять на величину выходного напряжения. Поэтому в схему частотного детектора обычно входит устройство для ограничения амплитуды входной э. д. с. Иногда ограничение осуществляется установлением специального режима работы усилительного прибора, входящего в состав частотного детектора.

В качестве линейной цепи можно использовать любую электрическую цепь, обладающую неравномерной частотной характеристикой: цепи RL, RC, фильтры, колебательные контуры и т. д. В высокочастотной технике большое распространение получили колебательные цепи. Схема частотного детектора, содержащего простой колебательный контур, представлена на рис. 8.36. Если резонансная частота контура сор отличается от средней частоты модулированного колебания ω₀, то изменение амплитуды напряжения на контуре U_к повторяет в известных пределах изменение частоты входного напряжения (рис. 8.37).

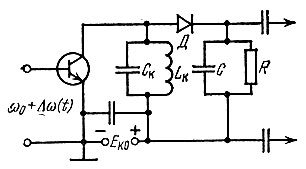
Рис. 8.36. Одноконтурный частотный детектор

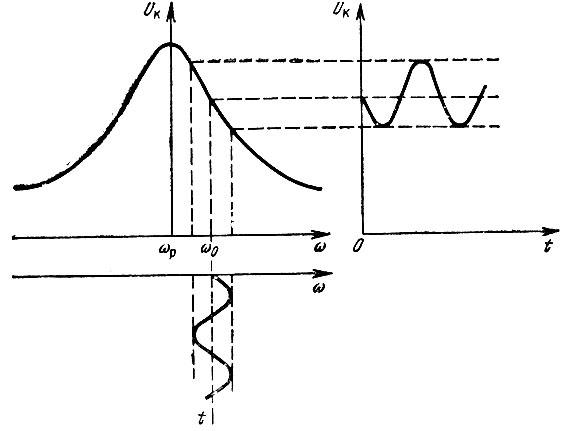
Рис. 8.37. К объяснению работы детектора, представленного на рис. 8.36

Изменение амплитуды U_к высокочастотного напряжения с помощью диода Д преобразуется в низкочастотное напряжение, которое выделяется на апериодической нагрузке R, С. Отметим попутно, что при точной настройке контура на частоту ω_p = ω₀ сигнал искажается; частота изменения огибающей получается вдвое выше частоты полезной модуляции. В исходном режиме, т. е. при отсутствии модуляции, рабочая точка должна устанавливаться на скате резонансной кривой.

Недостатком рассмотренной схемы является необходимость настройки контура на частоту, отличную от частоты немодулированного колебания. Кроме того, одиночный колебательный контур имеет весьма ограниченный линейный участок на скате резонансной кривой.

На рис. 8.38 представлена схема частотного детектора, широко распространенная в приемниках частотно-модулированных колебаний, а также в устройствах для автоматической подстройки частоты генераторов. Она содержит колебательную цепь в виде двух индуктивно связанных контуров, настроенных на частоту ω₀. Напряжение высокой частоты ω₀ ± Δω подается на базу транзистора, а продетектированное напряжение u_Ω выделяется на резисторах и R₂. Катушка индуктивности L_др (дроссель) преграждает путь току высокой частоты. Принцип действия данного детектора поясняется эквивалентной схемой и векторной диаграммой, представленными на рис. 8.39 и 8.40.

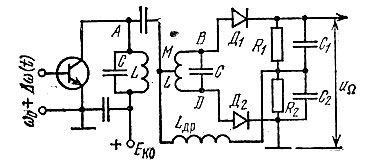
Рис. 8.38. Двухконтурный частотный детектор

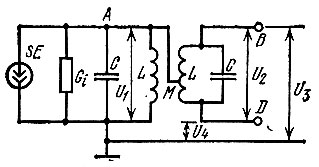
Рис. 8.39. Схема замещения избирательной цепи частотного детектора (к рис. 8.38)

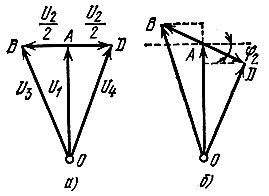
Рис. 8.40. Векторная диаграмма напряжений (к рис. 8.39)

Пусть U₁ - напряжение на первом контуре, U₂ - на втором контуре, U₃ и U₄ - напряжения в точках B и D относительно эмиттера (земли). Заметим, что U₃ и U₄ представляют собой амплитуды высокочастотных напряжений, приложенных соответственно к диодам Д₁ и Д₂. В отсутствие модуляции, когда частота входного напряжения совпадает с резонансными частотами контуров, напряжение U₂, развиваемое на индуктивности второго контура, сдвинуто по фазе на 90° относительно резонансного напряжения U_1р.

Действительно, при индуктивной связи двух одинаковых контуров имеем

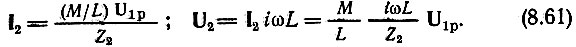
Так как при получаем

т. е. напряжение U₂ опережает напряжение U₁ на 90°.

Определим напряжения U₃ и U₄. Учитывая, что средняя точка второго контура присоединена по высокой частоте непосредственно к точке А и, следовательно, напряжение U₃ является суммой напряжения U₁ и половины напряжения U₂, получаем

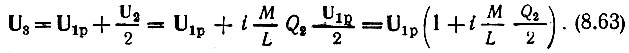
Аналогично для напряжения U₄ можем написать

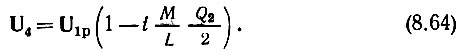
Модули напряжений U₃ и U₄ одинаковы и равны

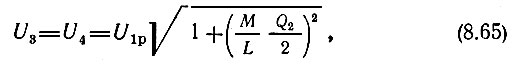
а фазы симметричны относительно фазы напряжения U_1р. Соответствующая этому случаю векторная диаграмма представлена на рис. 8.40, а. Так как выпрямленные напряжения U₀₁ и U₀₂, действующие на резисторах R₁ и R₂, пропорциональны амплитудам U₃ и U₄ то результирующее напряжение на выходе детектора, равное разности U₀₁ и U₀₂, при резонансной частоте будет равно нулю.

Рассмотрим теперь векторную диаграмму напряжений при расстройке. Пусть частота на входе детектора отклонится от резонансной частоты ω₀ на величину Δω, причем Δω/ω₀ << 1. Тогда вектор DB, соответствующий напряжению U₂ (рис. 8.40, б), повернется относительно своего резонансного положения на угол φ₂, который определяется выражением

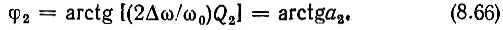
Вместо выражений (8.63) и (8.64) получим

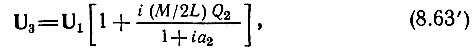
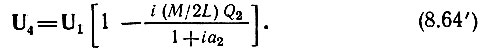
Первый и второй контуры обычно берутся идентичными. Поэтому отношение M/L = k является коэффициентом связи контуров. Кроме того, считаем Q₁ = Q₂ = Q, a₁ = а₂ = а.

Вводя обозначение

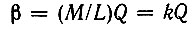
и переходя к модулям, получаем

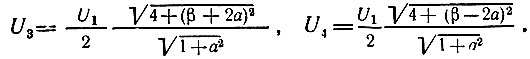
Напряжение на выходе при учете дифференциального включения нагрузок, а также формулы (8.50) будет

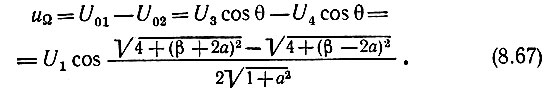
При учете соотношения 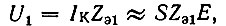а также зависимости Z_э1 от расстройки а формула (8.67) принимает следующий окончательный вид^*:

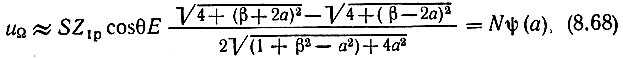
^* (Подробный вывод см. в предыдущем издании настоящей книги. М., "Сов. радио", 1971.)

где N = SZ_1p cos θE - постоянный коэффициент, а функция

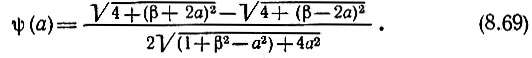
Зависимость ψ(а) представлена на рис. 8.41 в виде семейства характеристик для различных значений параметра β. Умножая ординаты этих характеристик на N, а абсциссы на f₀/2Q, получаем характеристику частотного детектора в виде зависимости u_Ω [В] от Δf [Гц].

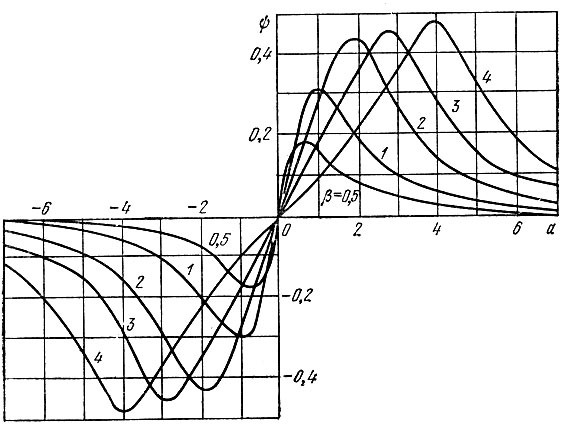
Рис. 8.41. Семейство характеристик двухконтурного частотного детектора: a = (2Q/f₀)Δf, β = (M/L)Q

При выборе параметров контуров и величины связи основным требованием является обеспечение линейности характеристики частотного детектора и максимально возможной ее крутизны.

Кроме рассмотренных, имеется ряд других схем частотных детекторов, отличающихся лишь в деталях.

Рассмотрим теперь принцип работы фазового детектора. Пусть фаза высокочастотного колебания, подлежащего детектированию, и меняется по закону θ(t). Если такое колебание подать на обычный частотный детектор, реагирующий на изменение мгновенной частоты колебания, то напряжение на выходе детектора

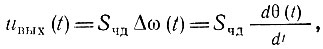
т. е. выходное напряжение, будет пропорционально производной фазы входного колебания. Отсюда видно, что для осуществления фазового детектирования можно использовать обычный частотный детектор. Необходимо лишь дополнить его корректирующей цепью осуществляющей интегрирование выходного напряжения, т. е. цепью с частотной характеристикой вида К(iω) = 1/iωτ₀. Простейшие интегрирующие устройства описаны в § 6. 5. Подобный прием используется при детектировании колебаний с медленно меняющейся фазой, т. е. когда производная фазы конечна (например, при передаче речи). В случае же скачкообразного изменения фазы, а также при необходимости сравнения фазы принимаемого колебания с фазой опорного (эталонного) колебания применяются специальные фазовые детекторы, в которых выходное напряжение пропорционально огибающей напряжения, получаемого при суммировании колебаний со сравниваемыми фазами, Подобные устройства рассматриваются в специальных курсах.