9.6. Нелинейное уравнение автогенератора

В предыдущих параграфах данной главы изучались условия возникновения колебаний и определялась устойчивость стационарного режима автогенератора. Необходимо рассмотреть весь процесс установления автоколебаний: от включения до установления стационарного режима. Это важно для ряда приложений, когда приходится иметь дело с формированием коротких радиоимпульсов (например, в импульсных радиосистемах). Для полного описания работы автогенератора, охватывающего все стадии процесса установления, необходимо отказаться от условия малости амплитуд, лежащего в основе линейного дифференциального уравнения (9.9').

Использованное при составлении этого уравнения линейное выражение (9.6)

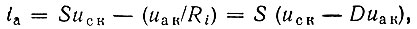
необходимо заменить нелинейной функцией

определяющей анодный ток i_а при любых значениях u_ск и u_ак.

Для дальнейшего исследования удобно перейти от схемы, изображенной на рис. 9.3, а, к схеме, показанной на рис. 9.16. Использованная в этой схеме параллельная схема замещения колебательного контура, не меняя сути дела, упрощает составление дифференциального уравнения для напряжения u_ак, действующего на контуре. При выбранных направлениях токов и напряжений можно написать следующие исходные уравнения:

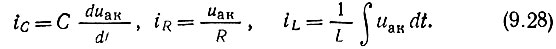
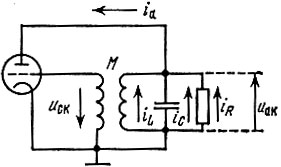
Рис. 9.16. Схема замещения автогенератора, соответствующая уравнению (9.29)

Подставляя выражения (9.26) и (9.28) в (9.27), получаем

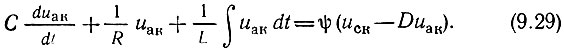
Преобразуем теперь аргумент нелинейной функции ψ, выразив u_ск через u_ак. Непосредственно из схемы с трансформаторной связью (рис. 9.16) вытекает соотношение u_ск = М (di_L/dt), а из третьего равенства (9.28) следует, что di_L/dt = u_ак/L. Следовательно, u_ск = u_акM/L.

Итак,

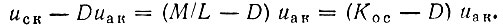
Заметим, что если не учитывать влияние u_ак на ток i_а (при D << К_ос), то u_ск ≈ К_осu_ак.

Введем обозначение

Тогда

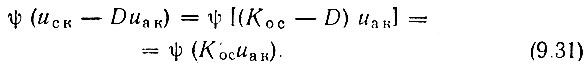
Подставляя это выражение в (9.29) и дифференцируя последнее по t, получаем

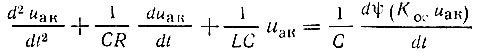
или

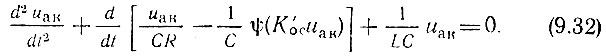
Как и следовало ожидать, получилось нелинейное уравнение. Дальнейший путь заключается в подстановке в уравнение (9.32) какой-либо подходящей аппроксимации функции ψ(К'_осu_ак).

Наиболее удобной является аппроксимация с помощью степенного полинома. Чтобы не слишком усложнять задачу, обычно исходят из неполного полинома третьей степени [см. (8.13)]:

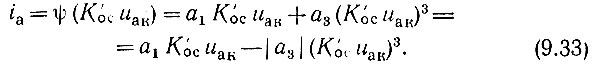
Входящее в выражение (8.8) слагаемое i(U₀) опущено, так как оно не оказывает влияния на поведение функции u_ак. Знак минус перед кубическим членом взят в соответствии с формулой (8.14).

Аппроксимация (9.33) пригодна при фиксированном положении рабочей точки на вольт-амперной характеристике (в точке перегиба, см. рис. 8.5). Следовательно, при этом не учитывается изменение напряжения смещения U₀ в процессе нарастания амплитуды колебания (при автоматическом смещении). Тем не менее, как показывает опыт, аппроксимация (9.33) все же позволяет выявить основные черты процесса установления колебаний в генераторе, работающем в мягком режиме.

Подставляя (9.33) в (9.32), получаем

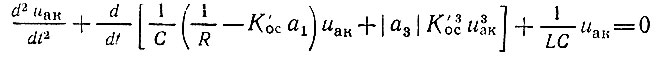
или

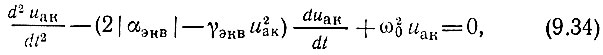
где использованы обозначения

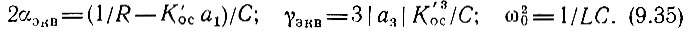
Заметим, что в самовозбуждающемся генераторе α_экв < 0 (см. § 9.2).

Разделив (9.34) на ω₀² и введя малый параметр

получаем

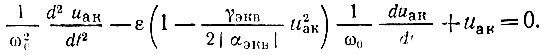
Переходя, наконец, к безразмерному времени τ = ω₀t, получаем уравнение, известное под названием уравнения Ван дер Поля:

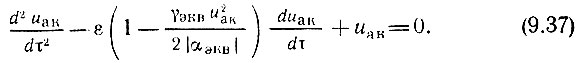
При малых напряжениях, когда 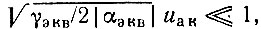уравнение (9.37) переходит в линейное уравнение, совпадающее с уравнением (9.9') при переходе в последнем к безразмерному времени, а также при учете различия между схемами на рис. 9.3 и 9.16]. С увеличением амплитуды напряжения u_ак все сильнее проявляется нелинейность системы, обусловленная величиной (γ_экв/2|α_экв|) u²_ак.

Методов, позволяющих получить точное решение нелинейного уравнения (9.37), не существует.