9.7. Приближенное решение нелинейного уравнения автогенератора

В применении к данной задаче суть приближенного метода заключается в том, что отыскивают решение нелинейного уравнения (9.37) в форме высокочастотного колебания

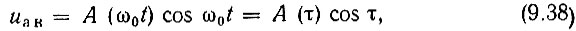
где ω₀ = ω_р - резонансная частота контура, т. е. 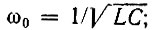А (τ) - функция, медленно изменяющаяся во времени.

Основанием для такого подхода является допущение высокой добротности колебательного контура, при которой для существенного изменения амплитуды и, следовательно, запасенной в контуре энергии требуется время, измеряемое значительным числом периодов. Условие медленности изменения амплитуды, сформулированное в § 3.1, предполагается выполненным.

Итак, для отыскания приближенного решения уравнения (9.37) остается найти только функцию А(τ), т. е. огибающую амплитуд колебания. Частота колебания просто приравнивается 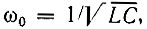а начальная фаза, которая в решении (9.38) опущена, может быть принята любой в зависимости от начальных условий запуска генератора^*.

^* (В действительности фаза, а следовательно, и частота колебания в процессе установления могут являться функциями времени. Для определения поправки к частоте необходимо находить второе или даже более высокие приближения.)

Подставим (9.38) в уравнение (9.37). Предварительно найдем производные от функции u_ак = А(τ) cos τ, для краткости опустим аргумент функции А(τ), а производную dA(τ)/dτ обозначим через А^⋅:

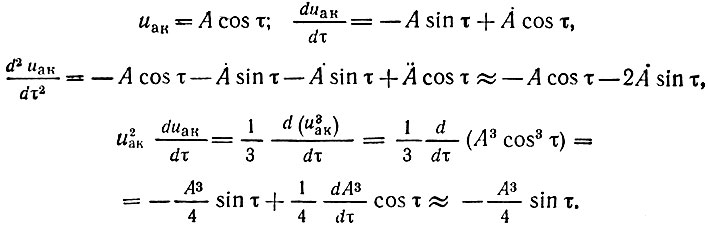
Слагаемое с 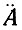отбрасывается, так как вторая производная медленно меняющейся функции является величиной второго порядка малости; слагаемое, содержащее cos 3τ = cos 3ω₀t, которое получается при возведении в куб cos τ отбрасывается, так как утроенная частота отфильтровывается колебательным контуром, настроенным на частоту ω₀. Кроме того, следует иметь в виду, что последнее слагаемое 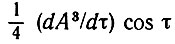после подстановки в уравнение (9.37) и умножения на малую величину ε также отбрасывается, как величина малая по сравнению со слагаемыми с коэффициентами A, A^⋅ или εA³. Произведение εA^⋅ cos 3ω₀ также отбрасывается. В результате уравнение (9.37) приводится к виду

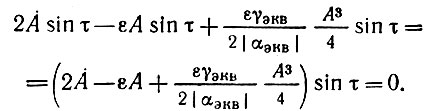
Так как sin τ ≠ 0, то приходим к следующему уравнению для амплитуды:

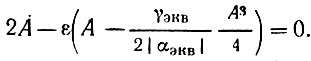
Умножая на A и учитывая, что 2AA = dA²/dτ, это уравнение в форме

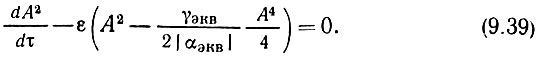
Получилось уравнение первого порядка относительно квадрата амплитуды. Стационарная амплитуда A_ст определяется сразу, достаточно приравнять нулю производную от A². Таким образом,

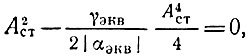
откуда

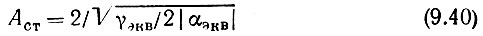
и уравнение (9.39) принимает вид

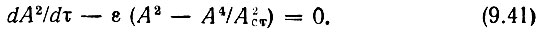
Для решения этого уравнения используется подстановка A² = 1/x. Тогда А²_ст = 1/х_ст и

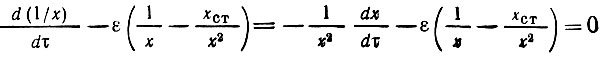
или

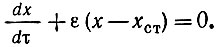
Разделяя переменные

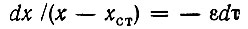
и интегрируя, получаем

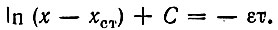
Пусть начальное значение амплитуды колебания в момент τ = 0 равно A₀. Тогда соответствующее этому моменту значение х₀ равно 1/A²₀. Полагая в последнем выражении τ = 0, находим постоянную интегрирования С:

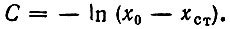
Следовательно,

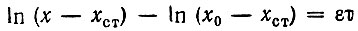
и

откуда

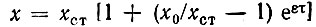
или

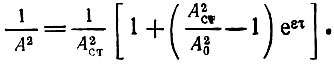
Наконец, учитывая выражение (9.36) и τ = ω₀t, а также то, что

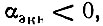
получаем

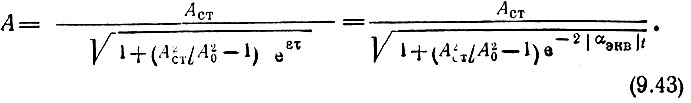
Подставляя это выражение в (9.38), получаем

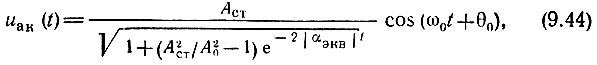
где θ₀ - начальная фаза, зависящая от условий запуска генератора.

Как правило, 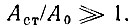Поэтому при малых значениях 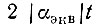знаменатель

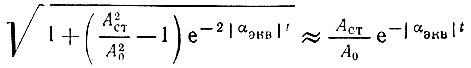
и выражение (9.44) принимает вид

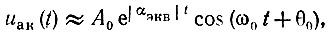
совпадающий с видом выражения (9.10), выведенного для линейного режима (при малых амплитудах).

При t → ∞ (стационарный режим)

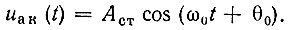
Ограничение амплитуд, обусловленное введением кубического члена в аппроксимацию вольт-амперной характеристики (9.33), иллюстрируется рис. 9.17, на котором представлен процесс установления колебания в автогенераторе.

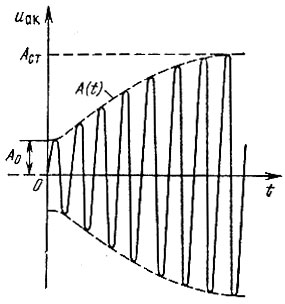
Рис. 9.17. Процесс установления колебания в автогенераторе

Характер изменения огибающей A(t)/A_ст при нескольких значениях параметра n = А_ст/А₀ показан на рис. 9.18.

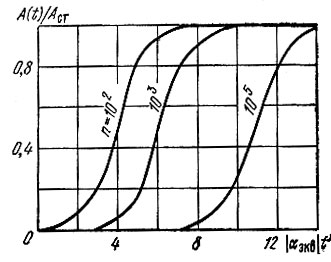
Рис. 9.18. Характер нарастания огибающей автоколебания при различных начальных условиях

Из выражения (9.43) и рис. 9.18 видно, что время установления стационарной амплитуды существенно зависит от начальной амплитуды, т. е. от начальных условий запуска. Это имеет важное значение для генераторов, работающих в импульсном режиме.

В заключение отметим, что для удовлетворительного описания процесса установления колебаний при жестком режиме самовозбуждения требуется удержание в полиноме (8.8) по крайней мере еще и пятой степени.