10.9. Двухчастотный параметрический усилитель

Принципиальная схема двухчастотного, или, как его часто называют, "двухконтурного" усилителя, изображена на рис. 10.20. Первый, сигнальный контур, настраивается на центральную частоту спектра сигнала (резонансная частота ω_р1 ≈ ω₁), а второй, "холостой" контур, - на частоту ω_р2, достаточно сильно отличающуюся от ω_р1.

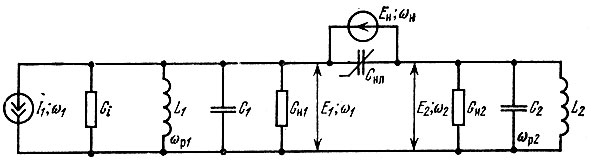
Рис. 10.20. Двухчастотный параметрический усилитель

Частота накачки выбирается из условия

При выборе частоты ω_р2 исходят из условия, что частота сигнала он находится вне полосы прозрачности вспомогательного контура. С другой стороны, комбинационная частота ω₂ = ω_н - ω₁ должна находиться вне рабочей полосы сигнального контура.

При выполнении этих условий на сигнальном контуре будет существовать лишь одно напряжение частоты ω₁, а на вспомогательном контуре - частоты ω₂. Считая амплитуды Е₁ и Е₂ этих напряжений малыми по сравнению с Е_н, можно заменить нелинейную емкость С_нл, совместно с генератором накачки, линейной параметрической емкостью, изменяющейся с частотой ω_н, как это было сделано в § 10.7. Тогда под воздействием напряжения сигнала е₁(t) = Е₁ cos (ω₁t + θ₁) в цепи переменной емкости С(t) = С₀ - ΔС cos (ω_нt + θ_н) возникает (помимо других составляющих, не представляющих в данном случае интереса) ток

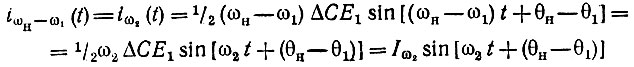
[см. выражение (10.59)]. Здесь I_ω2 = ¹/₂ω₂ΔСE₁.

На сопротивлении холостого контура Z₂(iω₂) = Z₂(ω₂) е^iφ_z ток i_ω2(t) создает падение напряжения

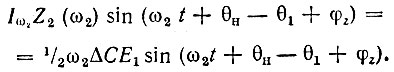
Эквивалентную э. д. с., воздействующую на емкость С(t), запишем, как и в § 10.5, в форме

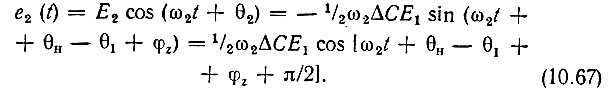
Комбинационный ток i_ωн-ω2(t), обусловленный этой э. д. с. будет

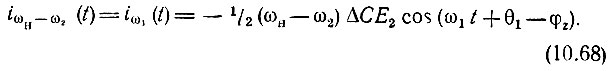
Как видим, по отношению к сигнальному контуру нелинейная емкость С_нл вместе с холостым контуром может быть замещена проводимостью, учитывающей ток

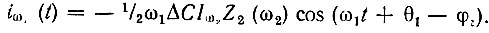
С учетом приведенного выше соотношения I_ω2 = (1/2) ω₂ΔСЕ₁ последнее равенство можно записать в форме

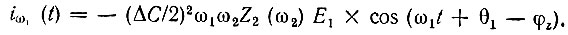
Комплексная амплитуда этого тока

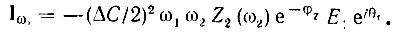
С другой стороны, комплексная амплитуда напряжения на сигнальном контуре е₁(t) = Е₁ cos (ω₁t + θ₁) равна Е₁ = Е₁е^iθ₁.

Следовательно, проводимость, шунтирующая сигнальный контур, будет

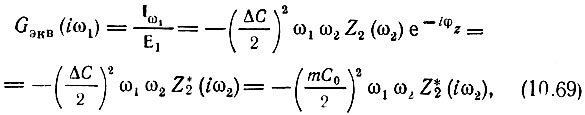
где 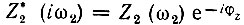- функция, комплексно-сопряженная функции Z₂(iω₂).

Для резонанса, когда ω₁ = ω_p1 и, следовательно, ω₂ = ω_р2, сопротивление вспомогательного контура будет R_н2 - 1/G_н2 и формула (10.69) принимает вид

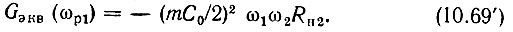
На схеме замещения, представленной на рис. 10.21, элементы, расположенные слева от штриховой линии, соответствуют сигнальному контуру усилителя, а справа - нелинейной емкости вместе со вспомогательным контуром. Полученная схема по существу совпадает со схемой одноконтурного усилителя (см. рис. 10.19). Различие лишь в способе определения эквивалентной отрицательной проводимости.

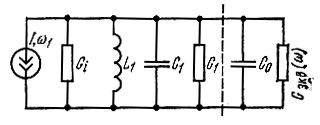
Рис. 10.21. Схема замещения двухконтурного параметрического усилителя

Следует отметить, что приведенные выше соотношения можно было бы получить более коротким путем, на основе выражений (10.44) -(10.56). Подробности, связанные с определением комбинационных колебаний 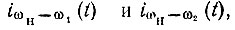приведены с целью привлечения внимания к следующим преимуществам двухконтурного усилителя:

а) эквивалентная отрицательная проводимость, а следовательно, и усиление мощности не зависят от фазы напряжения накачки;

б) не требуется соблюдение определенного соотношения между частотами ω₁ и ω_н.

Оба эти свойства двухконтурного усилителя объясняются тем, что полная фаза комбинационного тока i_ωн-ω2 в выражении (10.68), определяющая характер эквивалентной проводимости G_экв, по существу является разностью фаз напряжения накачки и е₂(t). Первая из них имеет вид (ω_нt + θ_н), а вторая (ω₂t + θ_н - θ₁) (без учета φ_z и π/2). При образовании разности θ_н выпадает, а разностная частота ω_н - ω₂ в любом случае совпадает с частотой сигнала (поскольку ω₂ = ω_н - ω₁).

Коэффициент усиления двухконтурного усилителя при резонансной частоте (ω₁ = ω_р1) можно определить из выражения, аналогичного формуле (10.63):

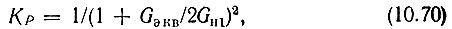
где G_экв вычисляется по формуле (10.69), а G_н1 - проводимость нагрузки сигнального контура.

При отклонении частоты сигнала ω₁ от резонансной частоты ω_р1 и соответственно частоты ω₂ от ω_р2 модуль сопротивления Z(iω₂) уменьшается, что приводит к уменьшению модуля G_экв и, следовательно, коэффициента усиления по мощности.

Основываясь на выражении (10.69), можно вычислить амплитудно-частотную характеристику и полосу пропускания двухконтурного усилителя.

Условие устойчивости усилителя в данном случае можно записать в форме

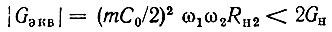
или

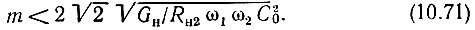
Рассмотрим энергетический баланс в двухчастотном усилителе в зависимости от соотношения частот ω₁ и ω₂.

Пусть заданы частота ω₁ и мощность Р_s сигнала на входе усилителя. Так как с повышением вспомогательной частоты ω₂ модуль отрицательной величины G_экв увеличивается [см. формулу (10.69)], то и усиление по мощности К_Р также растет [см. формулу (10.70)]. Мощность сигнала на выходе усилителя будет P_ω1 = K_PP_s.

Для определения требуемой мощности генератора накачки Р_ωн, а также мощности Р_ω2, выделяемой во вспомогательном контуре, воспользуемся теоремой Мэнли-Роу. На основании выражения (10.55) можно записать следующие соотношения:

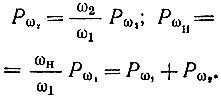
(Знак минус в последнем выражении опущен, так как очевидно, что эта мощность отбирается от генератора накачки.) Соотношение мощностей Р_s, Р_ω1, Р_ω2, Р_ωн иллюстрируется рис. 10.22. Из этого рисунка видно, что при ω₂ > ω₁ на вспомогательном контуре выделяется мощность, большая, чем на сигнальном. Таким образом, хотя с повышением частоты ω₂ мощность Р_ω1 и растет, распределение мощности, отбираемой от генератора накачки, изменяется в пользу частоты ω₂. Несмотря на это, часто работают в режиме ω₂ > ω₁, так как при усилении слабого сигнала основное значение имеет не степень использования мощности Р_ωн, а отношение мощности Р_ω1 к Р_s, т. е. усиление К_Р.

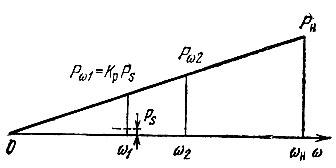
Рис. 10.22. Соотношение мощностей на различных частотах в двухконтурном параметрическом усилителе

Для иллюстрации количественных соотношений в двухчастотном параметрическом усилителе приведем следующий пример.

Пусть требуется осуществить усиление сигнала на частоте f₁ = 30 МГц при ширине спектра 2Δf₀ = 100 кГц.

Исходные данные первого (сигнального) контура: характеристика ρ₁ = 100 Ом; внутреннее сопротивление источника сигнала, шунтирующее контур, R_i = 5 кОм; сопротивление нагрузки R_н1 = 5 кОм.

Исходные данные второго (холостого) контура: резонансная частота f_p2 = 60 МГц; характеристика ρ₂ = 50 Ом; сопротивление нагрузки R_н2 = 5 кОм.

Прежде чем вычислять требуемую величину вариации емкости варикапа, найдем предельную величину проводимости G_экв, которую можно подключать к сигнальному контуру при заданной ширине спектра сигнала 2Δf₀.

Максимальная добротность сигнального контура (при шунтировании отрицательной проводимостью), очевидно, не должна превышать

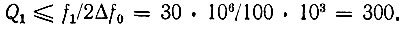
При ρ₁ = 100 Ом результирующая проводимость, шунтирующая первый контур, должна быть не менее

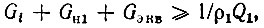
откуда

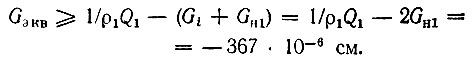
Подставляя значения G_экв, ω₁, ω₂ и R_н2 в формулу (10.69'), находим

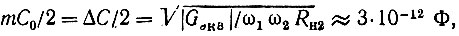
откуда

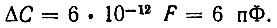
Требуемую величину ΔС можно реализовать с помощью обычного варикапа. Существующие в настоящее время варикапы допускают, например, изменение емкости до 30 пФ.

Коэффициент усиления мощности вычислим по формуле (10.70):

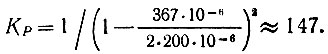
В заключение отметим основные преимущества и недостатки параметрического усилителя.

Важным преимуществом параметрического усилителя является относительно низкий уровень шумов по сравнению с транзисторным или ламповыми усилителями. В § 7.2 отмечалось, что главным источником шумов в транзисторном и ламповом усилителях является дробовой эффект, обусловленный хаотическим переносом дискретных зарядов электронов и дырок (в транзисторе). В параметрическом усилителе аналогичный эффект имеет место в приборе, осуществляющем модуляцию параметра. Так, например, изменение емкости варикапа происходит за счет перемещений электронов и дырок. Однако интенсивность потока носителей электричества в варикапе во много раз меньше, чем в транзисторе или лампе. В последних интенсивность потока определяет непосредственно мощность полезного сигнала, выделяемого в цепи нагрузки, а в варикапе - всего лишь эффект модуляции параметра. Ослабление влияния дробового эффекта столь значительно, что в параметрическом усилителе уровень шумов определяется в основном тепловыми шумами. В связи с этим часто применяют охлаждение параметрического диода до (5-10) К.

Недостатком параметрического усилителя является сложность развязки цепей накачки и сигнала.

В схеме, представленной на рисунке 10.18, а, характерной для параметрических усилителей метрового диапазона, развязка осуществляется с помощью разделительных конденсаторов и блокировочных дросселей. В диапазоне СВЧ, на которых особенно широко применяются параметрические усилители, приходится прибегать к весьма сложным конструкциям, сочетающим в одном узле двухчастотную колебательную цепь в виде полых резонаторов, варикап и специальные элементы развязки (циркулятор, направленный ответвитель, поглотитель, заградительный фильтр). Эти вопросы рассматриваются в специальных курсах.