10.8. Одноконтурный параметрический усилитель

Из предыдущего параграфа следует, что введением в колебательный контур переменной емкости или индуктивности можно при соответствующем законе изменения параметра осуществлять усиление колебаний. Простейшая схема одноконтурного параметрического усилителя с переменной емкостью изображена на рис. 10.18, а. Нелинейная емкость С_нл находится под воздействием двух напряжений: сигнального с частотой ω и управляющего с частотой ω_н.

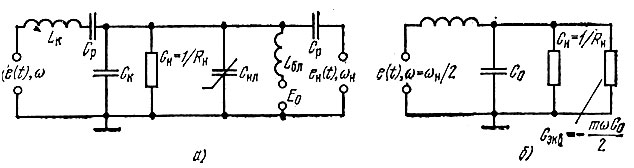
Рис. 10.18. Одноконтурный параметрический усилитель (а) и схема замещения (б)

Разделительные конденсаторы С_р защищают генератор накачки и источник сигнала от постоянного напряжения Е₀, используемого для установления рабочей точки на вольт-фарадной характеристике варикапа. Блокировочный дроссель преграждает путь и цепь источника Е₀ токам высокой частоты ω и ω_н.

Рассмотрим сначала режим работы усилителя при точном соблюдении условия

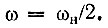
В этом, так называемом "синхронном" режиме комбинационная частота ω_н - ω совпадает с частотой ω, так что в контуре существует ток только на частоте ω. Схема замещения для синхронного режима представлена на рис. 10.18, б для случая γ = -π/2, соответствующего отрицательной вещественной проводимости G_экв.

Символом С₀ обозначена сумма С_к и средней емкости варикапа (соответствующей постоянному напряжению Е₀).

Для упрощения анализа источник э. д. с. сигнала е(t), включенный в контур последовательно, заменен на рис. 10.19 генератором тока, подключенным параллельно контуру и шунтированным внутренней проводимостью G_i. Проводимость нагрузки G_н включает в себя также проводимость, учитывающую потери мощности в элементах контура. Шунтирование проводимости нагрузки G_н отрицательной проводимостью G_экв = (ωΔС/2) sin γ = -ωΔС/2 = -mωС₀/2 уменьшает суммарную проводимость и таким образом повышает добротность контура. Получается эффект усиления.

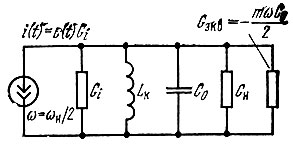
Рис. 10.19. Одноконтурный параметрический усилитель (рис. 10.18, а)

Составим выражение для коэффициента усиления в виде отношения мощности сигнала на выходе усилителя к максимальной мощности, которую можно получить при отсутствии параметрической модуляции.

Как известно, максимум мощности, выделяемой в проводимости нагрузки (при отсутствии усиления) достигается при G_н = G_i. При этом мощность сигнала равна

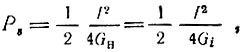
(I - амплитуда тока генератора).

При подключении дополнительной проводимости G_экв напряжение на выходе будет Е = I/(G_i + G_н + G_экв) = I/(2G_н + G_экв), а мощность, выделяемая в проводимости нагрузки.

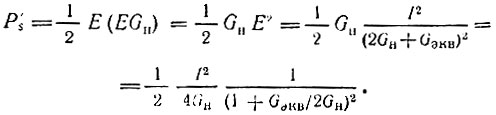
Отсюда коэффициент усиления по мощности

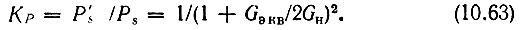
Напомним, что G_экв отрицательная величина.

Из этого выражения непосредственно вытекает условие устойчивости параметрического усилителя (в синхронном режиме):

откуда критическое значение коэффициента параметрической модуляции

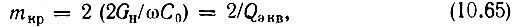
где Q_экв - добротность контура G учетом G_i и G_н = G_i.

Заметим, что при G_экв = -G_н, т. е. когда параметрическая модуляция компенсирует потери только в G_н, усиление по мощности равно всего лишь четырем.

На практике при усилении реального сигнала, фаза которого неизвестна, а частота может изменяться в некоторой полосе, соблюдение условий синхронного режима невозможно.

Пусть частота сигнала со будет не точно ω_н/2, а ω = ω_н/2 + Ω, где Ω - небольшое отклонение, не выходящее из полосы прозрачности колебательного контура. Тогда комбинационная частота будет

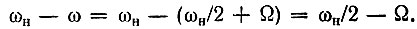
При этом в полосе пропускания контура оказываются два колебания: одно с частотой ω_н/2 + Ω (полезный сигнал) и другое с частотой ω_н/2 - Ω (комбинационная частота).

Соотношение между амплитудами указанных двух колебаний зависит от глубины модуляции емкости m и величины Ω. Подробный анализ, который здесь не приводится [2], показывает, что при значениях m, близких к критическому [см. формулу (10.65)1, и относительно малой расстройке Ω амплитуды обоих колебаний примерно одинаковы. Возникают биения и связанные с этим последствия (пульсация амплитуды и изменения фазы результирующего колебания). Можно, правда, показать, что даже при расхождении частот ω и ω_н/2, средняя за период биений мощность колебаний получается большей, чем при отсутствии параметрического воздействия, т. е. что и в этом, так называемом бигармоническим режиме, имеет место усиление сигнала. Однако подобный режим работы усилителя не всегда приемлем.

От недостатков, присущих одноконтурному параметрическому усилителю, свободна схема, рассматриваемая в следующем параграфе.