10.7. Схема замещения емкости или индуктивности, изменяющихся по гармоническому закону

Пусть к электронно-управляемой емкости (варикапу) приложено напряжение сигнала е(t) = Е cos ωt. Требуется определить ток, проходящий через источник сигнала. При этом предполагается, что частота управляющего колебания (генератора накачки) ω₀ приблизительно вдвое превышает частоту сигнала ω. Способ получения периодически изменяющейся емкости поясняется схемой на рис. 10.13, а. К нелинейной емкости С_нл подводится напряжение накачки е_у = Е_у cos (ω₀t + γ), наложенное на постоянное напряжение Е₀.

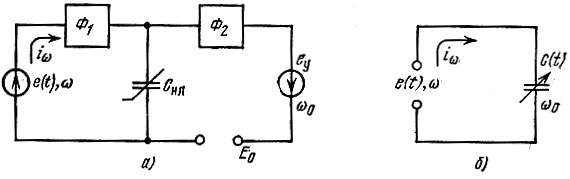
Рис. 10.13. Воздействие на линейную емкость напряжений накачки и сигнала (а) и схема замещения для слабого сигнала (б)

Фильтр Ф₁ преграждает путь току частоты ω₀ в цепь источника сигнала, а фильтр Ф₂ - току частоты сигнала ω (и близких к ω частот) в цепь накачки.

Наложим условие 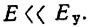Тогда, как указано в § 10.1, можно пренебречь изменением емкости под действием сигнала и считать, что закон изменения емкости определяется одним лишь управляющим напряжением. Основываясь на формуле (10.5), примем

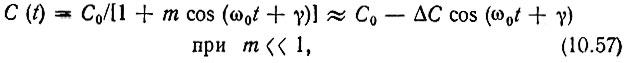
где

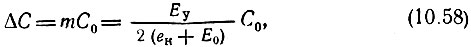
а γ - начальная фаза.

На рис. 10.13, б представлена эквивалентная линейная параметрическая схема, на которой цепь накачки не показана.

Определим полный ток через емкость С(t) с помощью общего выражения (10.7):

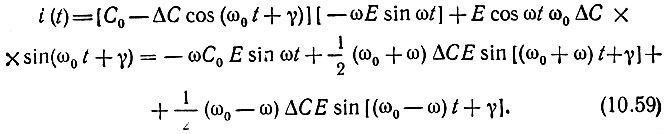
Заметим, что это выражение можно получить непосредственно из (10.51), если приравнять b₁ = С₀, Е₁ = Е, θ₁ = π/2, E₂ = Е_у, θ₂ = π/2 + γ, b₂E₂ = b₂E_у = ¹/₂ΔС, а также отбросить слагаемое с коэффициентом Е₁² (из-за малости) и слагаемые, не зависящие от Е₁.

Частота ω₀ + ω ≈ 3ω в полосу прозрачности фильтра Ф₁ не попадает; следовательно, ток в цепи источника сигнала является суммой двух токов: на частоте ω и на комбинационной частоте ω₀ - ω, бликой к ω (поскольку ω₀ на 2ω). Первый из этих токов, сдвинутый по фазе относительно е(t) = Е cos ωt на угол 90°, не может создавать активной проводимости - ни положительной, ни отрицательной. С точки зрения получения эффекта усиления интерес представляет комбинационное колебание разностной частоты ω₀ - ω, особенно в частном случае ω₀ = 2ω. При этом ток на частоте ω равен

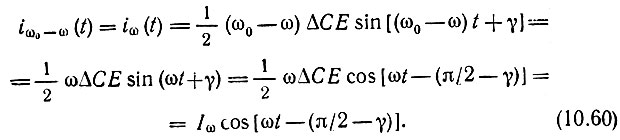
При э. д. с. источника сигнала е(t) = Е cos ωt и токе i_ω(t), определяемом выражением (10.60), отдаваемая источником мощность

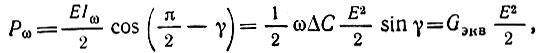
где символом

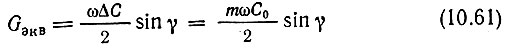
обозначена эквивалентная активная проводимость, учитывающая расход мощности источника сигнала.

Таким образом, приходим к схеме замещения (рис. 10.14, б), соответствующей параметрической цепи, показанной на рис. 10.14, а. Комбинационная частота ω₀ + ω = 3ω в этой схеме не учитывается, а частота ω₀ - ω совпадает с частотой ω. В результате по отношению к источнику сигнала параметрическая схема (рис. 10.14, а) приводится к схеме с постоянными параметрами. Периодическое изменение С(t) с частотой ω₀ = 2ω приводит лишь к появлению активной проводимости G_экв, шунтирующей постоянную емкость С₀.

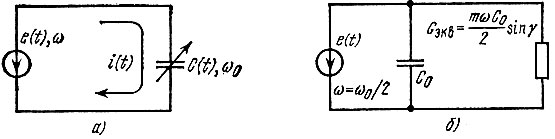
Рис. 10.14. Параметрическая емкостная цепь (а) и схема замещения для сигнала с частотой, вдвое меньше частоты накачки (б)

Рассмотрим три следующих характерных режима: γ = 0, π/2 и -π/2 (рис. 10.15), В первом случае (γ = 0) С(t) модулируется таким образом, что изменение запаса энергии в емкости за период частоты Т_ω0 = 2π/ω₀ (а также за период Т_ω = 2π/ω) равно нулю. При этом G_экв = 0.

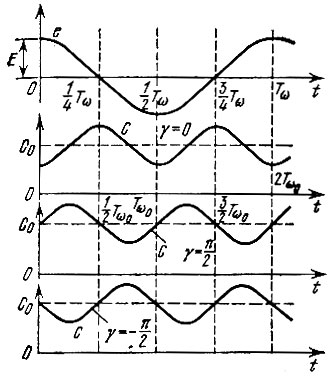
Рис. 10.15. Напряжение на емкости и законы ее изменения при различных начальных фазах

Во втором случае (γ = π/2) максимальная скорость нарастания С(t) соответствует амплитудным значениям напряжения; при этом часть энергии, запасенной в емкости, переходит в устройство, изменяющее емкость. По отношению к источнику э. д. с. это равносильно шунтированию постоянной емкости С₀ положительной активной проводимостью G_экв = (m/2) ωС₀.

Наконец, в третьем случае, при γ = -π/2, когда С(t) убывает в области е(t) = Е и нарастает в области е(t) = 0, активная проводимость отрицательна и равна G_экв = -(m/2) ωС₀.

Этот результат согласуется с результатами качественного рассмотрения принципа параметрического усиления (см. конец предыдущего параграфа). Отрицательная проводимость G_экв учитывает приток энергии от генератора накачки в цепь, содержащую С(t). В данном примере с электронно-управляемой емкостью прирост энергии, запасаемой в емкости, происходит за счет работы, совершаемой генератором накачки при уменьшении емкости (преодоление сил электрического поля при движении электронов и дырок через потенциальный барьер в области запирающего слоя).

Результаты, аналогичные полученным выше для С(t), нетрудно вывести также и для периодически изменяющейся индуктивности L(t).

Исходя из схемы (рис. 10.16, а), при изменении индуктивности по закону

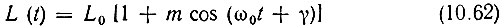
находим ток с помощью соотношения (10.11) (при m << 1):

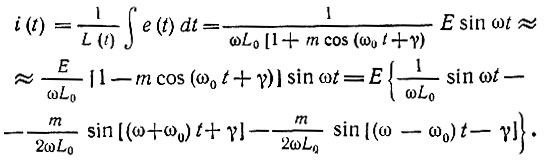
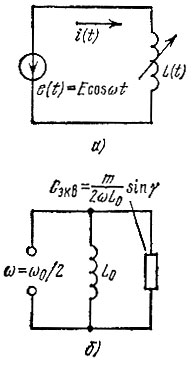
Рис. 10.16. Параметрическая индуктивная цепь (а) и схема замещения сигнала с частотой, вдвое меньшей частоты накачки (б)

При ω₀ = 2ω ток на частоте ω равен

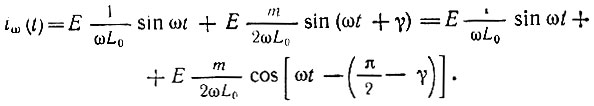
Первое слагаемое не определяет расхода мощности, а второе, сдвинутое относительно э. д. с. на угол π/2 - γ, определяет расход мощности

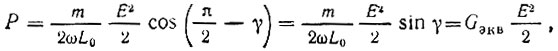
где

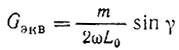
- активная проводимость.

Таким образом, при ω₀ = 2ω получается схема замещения, изображенная на рис. 10.16, б. Фазовые соотношения между е(t) = Е cos ωt, i(t) = (E/ωL₀) sin ωt и индуктивностью L(t), изменяющейся по закону (10.62), видны из рис. 10.17, построенного для γ = -π/2. В данном случае проводимость G_экв = - m/2ωL₀ получается отрицательной, если при прохождении тока через амплитудные значения функция L(t) убывает, а при прохождении i(t) через нуль L(t) возрастает.

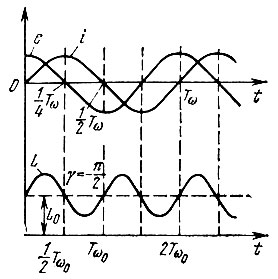
Рис. 10.17. Напряжение и ток в катушке, индуктивность которой убывает при наибольших значениях тока

Энергия вводится в цепь за счет работы, совершаемой устройством накачки при уменьшении индуктивности, обтекаемой током (на преодоление сил магнитного поля, стремящихся сблизить витки и увеличить индуктивность катушки).