10.6. Принцип параметрического усиления колебаний

В § 10.1 было показано, что по отношению к сигналу, малому по сравнению с управляющим колебанием, нелинейная емкость вместе с генератором накачки может быть замещена линейной, изменяющейся во времени емкостью. Отвлекаясь от способа осуществления модуляции емкости (или индуктивности), можно говорить об обмене энергией между сигналом и энергоемким параметрическим элементом.

Наглядным примером обмена энергией при изменении емкости является хорошо известная модель с механическим раздвижением пластин заряженного конденсатора. Пондеромоторная сила электрического поля конденсатора стремится сблизить пластины (независимо от полярности напряжения); следовательно, для их раздвижения, т. е. для уменьшения емкости, необходимо произвести работу, которая увеличивает запас энергии конденсатора. При сближении пластин, наоборот, часть энергии поля конденсатора преобразуется в механическую энергию. Нетрудно установить связь между относительным изменением емкости конденсатора и изменением запаса энергии.

Рассмотрим конденсатор, емкость которого С(t) изменяется по скачкообразному закону, представленному на рис. 10.11. Пусть конденсатор получил заряд q, который затем остается постоянным (конденсатор без утечки, в разомкнутой цепи). В моменты времени, соответствующие мгновенному уменьшению емкости на величину ΔC = C₁ - С₂, напряжение на конденсаторе возрастает на величину Δu = u₂ - u₁ = q (1/С₂ - 1/C₁) = q (С₁ - С₂)/С₁С₂ = u₁ΔС/С₂, а энергия - на величину ΔЭ = Э₂ - Э₁ = (q²/2) × (1/С₂ - 1/С₁) = (q²/2C₁) ΔС/С₂ = Э₁ΔС/С₂. В момент скачкообразного увеличения емкости напряжение и энергия уменьшаются соответственно на Δu и ΔЭ.

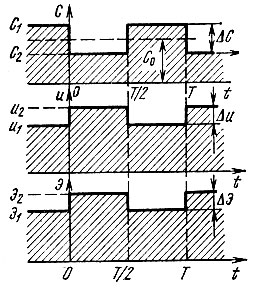
Рис. 10.11. Напряжение на конденсаторе и запасаемая энергия при скачкообразном изменении емкости. Заряд конденсатора постоянный

В первом случае дополнительная энергия ΔЭ черпается из устройства, осуществляющего скачок емкости (вниз), а во втором случае, при увеличении емкости, происходит обратное преобразование энергии. В среднем, за время Т, энергия конденсатора остается неизменной.

Иначе обстоит дело, если заряд конденсатора является функцией времени, причем такой, что уменьшение емкости производится в моменты максимума q(t), а увеличение - в моменты минимума (еще лучше в моменты прохождения q(t) через нуль). Такой режим работы можно реализовать при включении конденсатора С(t) в контур, частота колебаний в котором вдвое меньше частоты изменения емкости. Допустим, что высокодобротный контур возбуждается сигналом е(t) = Е cos ωt, частота которого совпадает с резонансной частотой контура 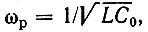отвечающей условию ω_р = 2πf_р = 2π/2T, где Т - полный цикл изменения С(t). Тогда напряжение на контуре можно представить в виде колебания, очень близкого к гармоническому, но получающего приращение в моменты спада С(t) (рис. 10.12). Это равносильно увеличению мощности сигнала. Если прирост энергии, обусловленный одним скачком (вниз) емкости С(t), не превышает расхода энергии за время T, то параметрическая цепь устойчива, в противном случае - возникает параметрическое возбуждение колебаний. Таким образом, регулируя относительную величину ΔС/С₀, т. е. глубину модуляции параметра С, можно осуществить как параметрическое усиление сигнала, так и параметрическую генерацию.

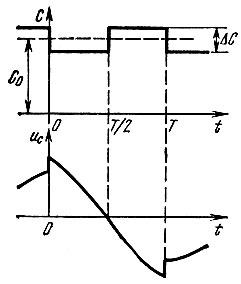
Рис. 10.12. Увеличение амплитуды напряжения на конденсаторе в моменты скачкообразного уменьшения емкости

Реализация скачкообразного изменения С(t) связана с техническими трудностями и в практике не применяется. Значительно проще модулировать емкость по гармоническому закону. Необходимо лишь соблюдать основной принцип: уменьшать емкость в области максимальных значений заряда (напряжения) конденсатора и увеличивать в области минимальных значений.

В последующих параграфах изучаются схемы замещения энергоемких элементов С и L, изменяющихся во времени по гармоническому закону, и устанавливаются основные соотношения, необходимые для аналитического описания процессов усиления и генерации в параметрических цепях.