10.5. Энергетические соотношения в цепи с нелинейным реактивным элементом при гармонических колебаниях

В § 10.1 отмечалось, что электронный способ осуществления переменной емкости (линейной) основан на применении нелинейной емкости, находящейся под воздействием управляющего колебания.

Особенностью бигармонического воздействия (сигнал и управляющее колебание) на нелинейный реактивный элемент является обмен энергией между источниками отдельных колебаний. Расходуемая в параметрической цепи энергия поставляется ("накачивается") источником управляющего колебания. В связи с этим его часто называют генератором накачки, а управляющее колебание - напряжением накачки. Управляющее колебание наряду с обозначением е_y(t) = Е_у cos (ω_уt + θ_у) в дальнейшем часто будет записываться в форме е_н(t) = Е_н cos (ω_нt + θ_н).

Рассмотрим воздействие на нелинейную емкость С_нл (варикап) двух гармонических колебаний (рис. 10.9):

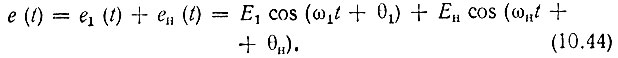
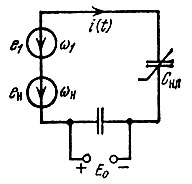
Рис. 10.9. Бигармоническое воздействие на нелинейную емкость

Вольт-кулонную характеристику варикапа аппроксимируем, как и в § 10.1, полиномом второй степени

где b₁ = С₀ определяется выражением (8.4), а

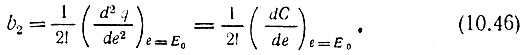
Применяя первое выражение (8.3) к ряду (10.45), находим ток через нелинейную емкость

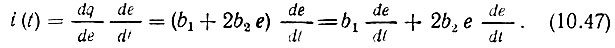
Подставляя в это уравнение внешнее воздействие (10.44), после несложных тригонометрических преобразований получаем окончательное выражение

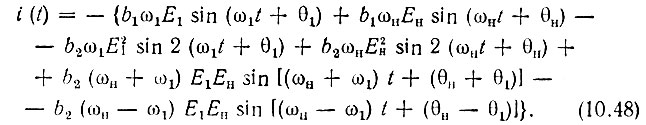
Два первых слагаемых в полученном выражении соответствуют токам частот ω₁ и ω_н, которые имели бы место при линейной емкости, равной b₁, остальные слагаемые - гармоники с частотами 2ω₁, 2ω_н и комбинационные колебания с частотами ω_н + ω₁, ω_н - ω₁ являются продуктом взаимодействия двух гармонических колебаний в квадратичной нелинейности.

Заметим, что по своему составу спектр тока через нелинейную емкость отличается от спектра тока через резистивный нелинейный элемент только отсутствием постоянной составляющей [см. (8.28)-(8.30)].

Рассмотрим энергетические соотношения. Первые два тока (с коэффициентами b₁), сдвинутые по фазе на 90° относительно соответствующих э. д. с. е₁(t) и е_н(t), не создают расхода энергии (как и в обычном линейном конденсаторе без потерь). Ток с частотой ω_н + ω₁ может также не учитываться при энергетических расчетах, так как средняя мощность, отдаваемая генератором э. д. с. частоты ω₁ или ω_н при протекании через них тока с частотой ω_н + ω₁, равна нулю.

Нагрузка же генераторов, создаваемая остальными токами с частотами 2ω₁, 2ω_н и ω_н - ω₁ зависит от соотношения фаз θ₁ и θ_н. Если частоты ω₁ и ω_н находятся в кратном соотношении, совпадающем со степенью аппроксимирующего полинома (т. е. с порядком нелинейности), то при определенном соотношении фаз θ₁ и θ_н эти токи могут оказаться в фазе (или в противофазе) с электродвижущими силами е₁(t) или е_н(t).

В частности, в рассматриваемом случае квадратичной нелинейности, при выполнении условия ω_н = 2ω₁, комбинационная частота ω_н - ω₁ совпадает с частотой э. д. с. ω₁ (соответственно при ω₁ = 2ω_н |ω_н - ω₁| = ¹/₂ω₁ = ω_н). При этом токи с частотами 2ω_н и ω_н + ω₁ можно не учитывать, токи же с частотами ω_н и ω₁ представим в виде

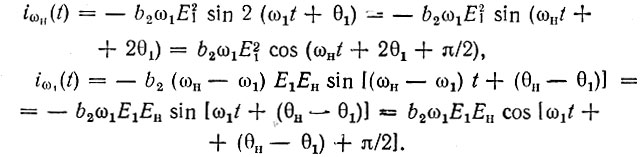
Так как ток i_ωн(t) сдвинут по фазе относительно е_н(t) = Е_н × cos (ω_нt + θ_н) на угол θ_н - (2θ₁ + π/2) = θ_н - 2θ₁ - π/2, то средняя мощность, отдаваемая генератором э. д. с. е_н(t), будет равна

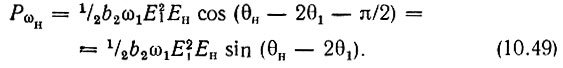
Соответственно мощность, отдаваемая генератором на частоте ω₁ при сдвиге фаз θ₁ - [(θ_н - θ₁) + π/2] = 2θ₁ - θ_н - π/2,

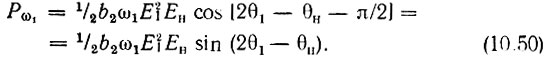
Заметим, что при любых фазах θ₁ и θ_н выполняется условие

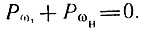
Наложим теперь на фазы добавочное условие: θ_н - 2θ₁ = π/2. Тогда Р_ωн - положительна, a P_ω1 - отрицательна. Это означает, что генератор э. д. с. частоты ω₁ не расходует мощности, а наоборот, потребляет ее от генератора частоты ω_н.

Пусть теперь θ_н - 2θ₁ = -π/2. Тогда Р_ωн < 0, а Р_ω1 > 0 и источником энергии является генератор частоты ω₁, а потребителем - генератор э. д. с. частоты ω_н.

Рассмотрим теперь энергетические соотношения в цепи, содержащей кроме нелинейной емкости С_нл еще и линейный, диссипативный элемент - параллельный колебательной контур, настроенный на частоту, близкую к ω₂. На рис. 10.10 этот элемент обозначен символом Z₂(iω₂) (комплексное сопротивление).

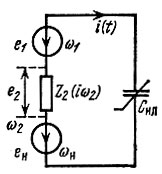
Рис. 10.10. Бигармоническое воздействие на цепь с нелинейной емкостью и параллельным колебательным контуром, настроенным на комбинационную частоту

На нелинейную емкость воздействуют две электродвижущие силы от независимых источников - сигнал е₁(t) = Е₁ cos (ω₁t + θ₁) и напряжение накачки e_н(t) = Е_н cos (ω_нt + θ_н) и, кроме того, напряжение комбинационной частоты ω₂ = ω_н - ω₁, являющееся продуктом взаимодействия е₁(t) и е_н(t) в нелинейной емкости. Запишем это напряжение в форме е₂(t) = Е₂ cos (ω₂t + θ₂), имея в виду, что амплитуда Е₂ и фаза θ₂, зависящие не только от колебаний е₁(t) и е_н(t), но и от комплексного сопротивления Z₂(iω₂), требуют еще определения. В дальнейшем будем исходить из условия, что сопротивление Z₂(iω₂) для частот ω₁ и ω_н пренебрежимо мало.

Подставляя в выражение (10.47)

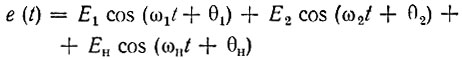
и производя несложные выкладки, получаем формулу, аналогичную (10.48) (частоты, отличные от ω_н - ω₂ = ω₁, ω_н - ω₁ = ω₂ и ω₁ + ω₂ = ω_н, не учитываются):

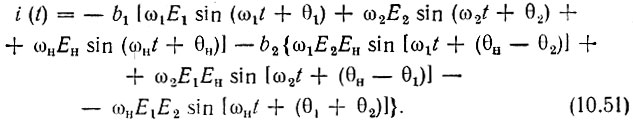
При определении энергетического баланса три первых слагаемых (с коэффициентами b₁) можно не учитывать [см. комментарий к формуле (10.48)]. Токи же частот ω₁, ω₂ и ω_н, возникающие из-за нелинейности вольт-кулонной характеристики, определяются выражениями

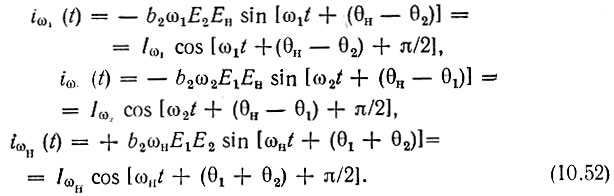
Здесь 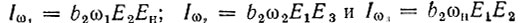представляют собой амплитуды токов i_ω1(t), i_ω2(t) и i_ωн(t).

Учитывая, что в исходных выражениях е₂(t) = Е₂ cos (ω₂t + θ₂) имеет смысл э. д. с., компенсирующей падение напряжения на сопротивлении Z₂(iω₂) при прохождении через него тока i_ω2(t), можем на основании второго равенства (10.52) составить следующее выражение:

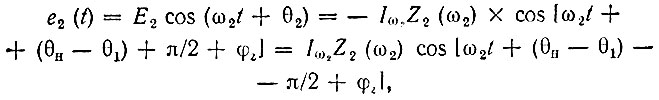
где через φ_z обозначен аргумент сопротивления z₂(iω₂). Отсюда следует, что

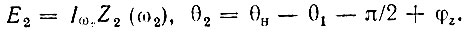
На основании последнего выражения формулы (10.52) можно привести к следующему виду:

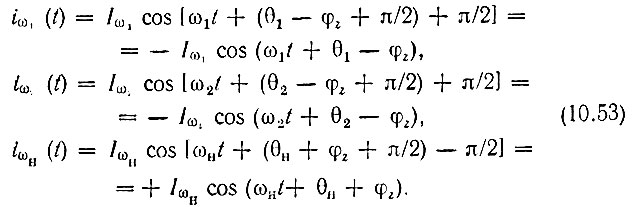
Составим выражения для мощностей, выделяемых в нелинейной емкости на частотах ω₁, ω₂ и ω_н:

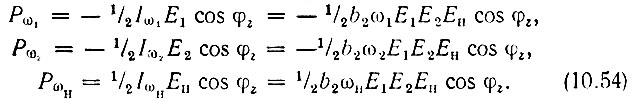
Отрицательные значения P_ω1 и P_ω2 означают, что соответствующие источники э. д. с. е₁(t) и e₂(t) не отдают, а потребляют энергию. Положительное же значение Р_ωн указывает на то, что при выбранных частотах (ω_н > ω₂, ω_н > ω₁) источник е_н(t) отдает энергию во внешнюю цепь.

Суммарная мощность, выделяемая в нелинейном реактивном элементе,

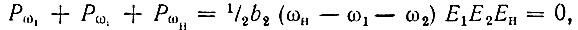
поскольку ω_н = ω₁ + ω₂. Этот результат находится в полном согласии с принятым допущением отсутствия потерь в емкости.

Из выражений (10.54) получаем следующие пропорции:

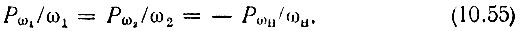
Эти соотношения являются частным случаем общей теоремы Мэнли-Роу об энергетических соотношениях в спектре колебания в цепи, содержащей реактивную нелинейность. Эта теорема записывается в форме

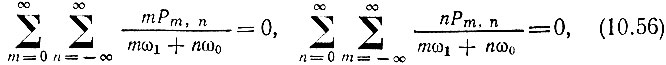
где ω₁ и ω₀ - частоты генераторов, возбуждающих систему; Р_{m, n} - мощность колебания частоты mω₁ + nω₀; целые числа m и n определяют порядок комбинационного колебания. Предполагается, что в общем случае в цепи с нелинейной реактивностью имеются проводимости для любых комбинационных частот.

Выражения (10.56) можно распространить на любые реактивности - емкостные и индуктивные - при условии отсутствия гистерезиса.

Первое равенство (10.56), в котором m принимает только положительные значения, устанавливает соотношение между мощностью Р_{m, n} комбинационного колебания и частотой генератора ω₁. Соответственно второе равенство, в котором n ≥ 0, устанавливает связь между комбинационными колебаниями и частотой ω₀ второго генератора.

Поясним применение выражений (10.56) на примере рассмотренной ранее цепи (рис. 10.10), возбуждаемой двумя генераторами на частотах ω₁ и ω₀ = ω_н. Кроме этих частот, на пассивном элементе Z₂(ω₂) создается одно комбинационное колебание с разностной частотой ω₂ = ω_н - ω₁.

В соответствии с обозначениями выражений (10.56) частоту ω₁ следует рассматривать как значение знаменателя mω₁ + nω₀ при m = 1 и n = 0, а мощность на этой частоте P_ω1 = Р_{1, 0}. Частоте ω₀ соответствуют индексы суммирования m = 0, n = 1 и мощность Р_ω0 = Р_{0, 1}. Наконец, частоте ω₂ = ω₀ - ω₁ соответствуют индексы m = -1, n = 1 и мощность Р_ω2 = Р_ω0-ω1 = Р_{-1, 1}.

Тогда внутренняя сумма в первом равенстве (10.56) дает

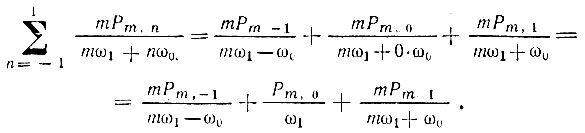
Суммируя полученное выражение по m, получим первое равенство (10.56)

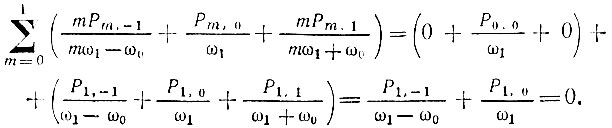
(Слагаемые, содержащие Р_{0, 0} и Р_{1, 1}, отброшены). Таким образом,

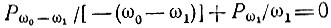
или

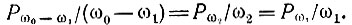
Аналогичным образом второе равенство дает

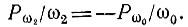
Итак, получаем пропорции

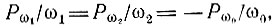
совпадающие с выражением (10.55) при замене ω₀ на ω_н.

Из проведенного анализа видно, что с помощью нелинейной емкости можно осуществить преобразование спектра, сопровождающееся перекачкой энергии из одного источника в другой. Так, если ω₁ - частота принимаемого сигнала, а ω₀ - частота генератора накачки, то можно выделить комбинационную частоту ω₂ = ω₀ - ω₁ с одновременным усилением мощности колебания на этой частоте. Напомним, что при использовании резистивного нелинейного элемента преобразование частоты сигнала (см. § 8.10) не сопровождается перекачкой энергии от гетеродина.