10.4. Определение импульсной характеристики параметрической цепи

Для определения импульсной характеристики g(t, х) непосредственно по заданным параметрам цепи, без обращения к передаточной функции К(iω, t), необходимо использовать дифференциальное уравнение цепи.

Рассмотрим сначала простую цепь, описываемую уравнением первого порядка

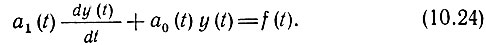
По определению импульсная характеристика является откликом цепи на единичный импульс δ(t - х), подаваемый на вход в момент t = х (см. § 10.2). Из этого определения следует, что если в правой части уравнения (10.24) функцию f(t) заменить на δ(t - х), то в левой части y(t) можно заменить на g(t, х).

Таким образом, приходим к уравнению

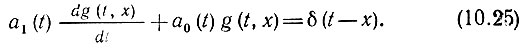
Так как правая часть этого уравнения равна нулю всюду, кроме точки t = х, функцию g(t, х) можно искать в виде решения однородного уравнения (с нулевой правой частью)

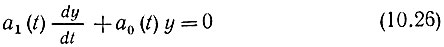
при начальных условиях, вытекающих из уравнения (10.25), а также из условия, что к моменту приложения импульса δ(t - х) в цепи отсутствуют токи и напряжения ("пустая" цепь).

В уравнении (10.26) переменные разделяются:

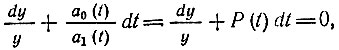
откуда

где

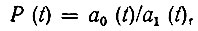
а

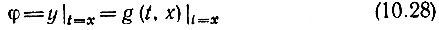
представляет собой значение импульсной характеристики в момент t = х.

Для определения φ вернемся к исходному уравнению (10.25), из которого видно, что в точке t = х функция g(t) должна совершать скачок на величину 1/а₁(х) (рис. 10.5). Только при этом условии первое слагаемое в уравнении (10.25), т. е. a₁(t)dg/dt, может образовать дельта-функцию δ(t - x).

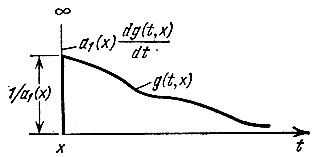
Рис. 10.5. Импульсная характеристика цепи, описываемой уравнением (10.25)

Так как при t < х g(t, х) = 0, то в момент t = х

Заменяя в выражении (10.27) неопределенный интеграл определенным с переменным верхним пределом, получаем

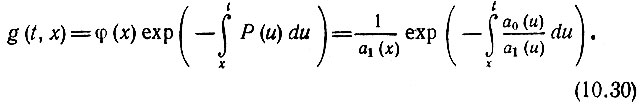
Для ясности переменная интегрирования в отличие от t обозначена буквой u.

Используем выражение (10.30) для цепи (рис. 10.6), представляющей собой последовательное соединение резистора с постоянным сопротивлением r и конденсатора с емкостью С(t), изменяющейся по закону

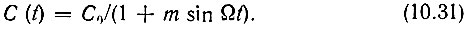
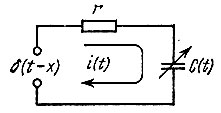
Рис. 10.6. Пример простой параметрической цепи

Под δ(t - х) в данном случае подразумевается единичный импульс э. д. с., а в качестве функции g(t, x), подлежащей определению, выберем заряд конденсатора q(t).

Тогда уравнение цепи в соответствии с (10.25) и (10.31) можно записать в форме

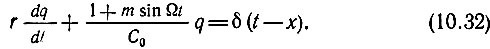
Подставляя в (10.30)

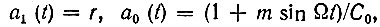
получаем

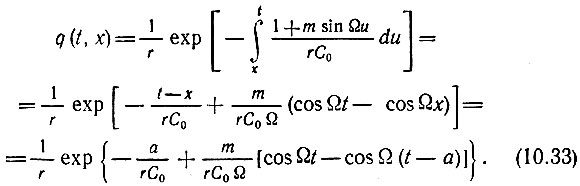
Продифференцировав это выражение по t, можно найти ток i(t). В момент t = х (т. е. при а = 0), когда q(t, x) образует скачок, равный 1/r, ток будет (1/r) δ(t - х), а напряжение на сопротивлении - δ(t - х). Напряжение же делением выражения (10.33) на С(t).

Из выражения (10.33) видно, как вариация емкости по закону (10.30) влияет на характер разряда: в аргументе экспоненты кроме - (t - х)/rС₀ (как и при постоянной емкости С₀) появляется периодическое слагаемое [m/rC₀Ω] × [cos Ωt - cos(t - а)].

Закон изменения С(t)/C₀ показан на рис. 10.7, а, график функции rq(t, х) при rС₀Ω = 1 и m = 0,25 - на рис. 10.7, б. Отсчет безразмерного времени Ωt на рис. 10.7, б ведется от момента Ωx = π/2, соответствующего прохождению С(t)/C₀ через минимум. Штриховой линией показана зависимость 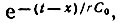соответствующая импульсной характеристике цепи при постоянной емкости С₀ (m = 0).

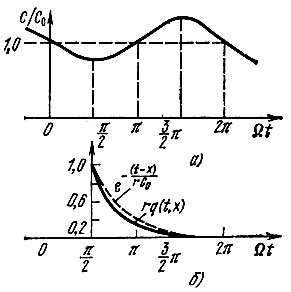
Рис. 10.7. Закон модуляции емкости (а) и импульсная характеристика цепи (б), показанной на рис. 10.6

Обратимся теперь к общему случаю - цепи, описываемой уравнением n-го порядка:

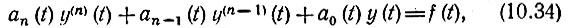
в котором все коэффициенты а_n, a_n-1, ..., а₀ могут являться функциями δ(но не y).

Как и в предыдущем случае, приравниваем f(t) дельта-функции (t - х), что позволяет переписать уравнение (10.34) в форме

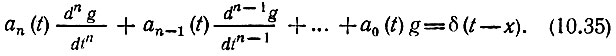
Импульсную характеристику ищем в виде решения однородного уравнения

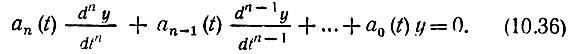
Общее решение этого уравнения представляет собой сумму из n линейно независимых решений

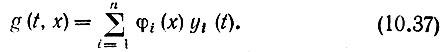
Для определения функций φ_i(х) можно использовать начальные условия, вытекающие из уравнения (10.34).

В отличие от рассмотренного уравнения (10.25) в данном случае необходимо в точке t = х приравнять нулю все производные функции g(t, х) порядка не выше n - 2. Производная же порядка n - 1 в точке t = x должна совершать скачок на величину 1/а_n(х) (рис. 10.8).

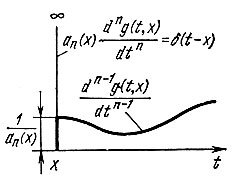
Рис. 10.8. Импульсная характеристика цепи, описываемой уравнением (10.35)

При этих начальных условиях выражение (10.37) образует систему уравнений (при дифференцировании по t и подстановке t = х)

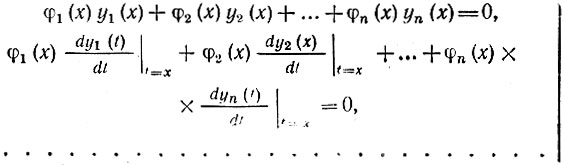
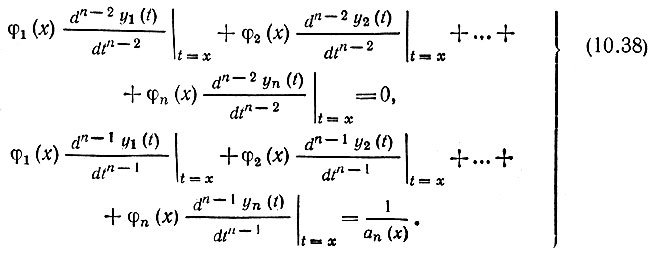
Так как частные решения y_i(t) и их производные в точке t = х предполагаются известными, то система (10.38), содержащая n уравнений, позволяет найти все функции φ_i(x). Системе уравнений (10.38) соответствует определитель

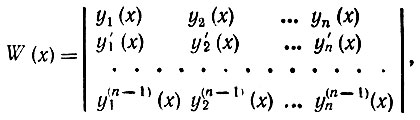
называемый определителем Вронского.

Применяя правило Крамера, получаем следующее общее выражение для φ_i(х):

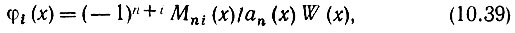
где M_ni(x) - минор, получаемый из определителя W(x) вычеркиванием n-й строки (соответствующей производным порядка n - 1) и столбца i, на пересечении которых стоит элемент y^(n-1)(x).

Подставляя (10.39) в общее решение (10.37), получаем

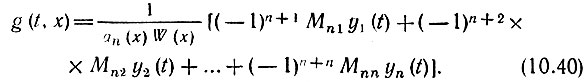
Выражение, стоящее в квадратных скобках, можно рассматривать как разложение соответствующего определителя по строке y₁(t), y₂(t), ..., y_n(t). Обозначив этот новый определитель через d, можем написать

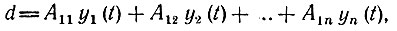
откуда вытекает следующее равенство для алгебраических дополнений А_1i:

С другой стороны, в искомом определителе d алгебраические дополнения А_1i связаны с соответствующими им минорами М^d_1i соотношением

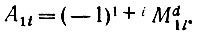
Следовательно, миноры нового определителя выражаются через миноры определителя Вронского с помощью следующей формулы:

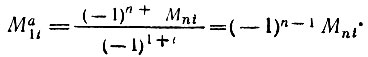
Но минор М_ni, как уже отмечалось, получается из определителя Вронского вычеркиванием i-го столбца и строки, соответствующей производным порядка n - 1. Поэтому искомый определитель d должен иметь вид

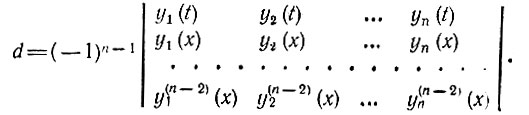
Таким образом, окончательно

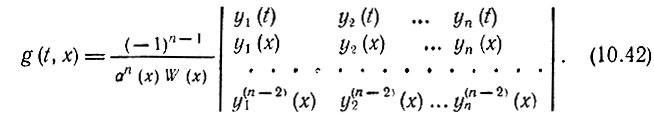
Определяемая выражением (10.42) функция g(t, х) есть не что иное, как односторонняя функция Грина линейного дифференциального оператора

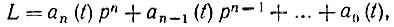
соответствующего уравнению (10.34).

В теории линейных неоднородных уравнений функция Грина используется для представления решения уравнения (10.34) в форме

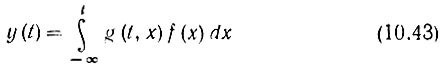
при начальных условиях y^(k)(0) = 0, k = 0, 1, ..., (n - 1). Выражение (10.43) совпадает с (10.13).