10.3. Модуляция как параметрический процесс

В § 8.12 рассматривался способ получения АМ колебания, основанный на изменении импульса тока в нелинейном резонансном усилителе. Не следует, однако, думать, что осуществление модуляции является нелинейным процессом. По существу, указанный выше способ модуляции можно трактовать как пропускание несущего колебания через параметрический четырехполюсник, передаточная функция которого изменяется по закону модулирующего напряжения. (Изменение импульса тока, а следовательно, и средней крутизны S_cp приводит к изменению коэффициента усиления цепи.) Таким образом, если отвлечься от способа управления параметрами цепи, модуляцию следует рассматривать как параметрический процесс. Иллюстрацией к сказанному может служить пример преобразования спектра в простейшей параметрической цепи, приведенный в § 1.5.

Аналогичное рассуждение можно привести для угловой модуляции. Пусть требуется получить колебание вида a(t) = А₀ cos [ω₀t + θ(t) + θ₀], где θ(t) - фаза, модулированная по заданному закону. Рассматривая а(t) как колебание на выходе линейного параметрического четырехполюсника, на вход которого подается несущее колебание е(t) = Е₀ cos ω₀t, найдем передаточную функцию этого четырехполюсника. 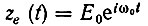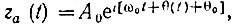Для этого перейдем от заданных функций е(t) и а(t) к комплексным колебаниям соответственно и после чего используем формулу (10.16):

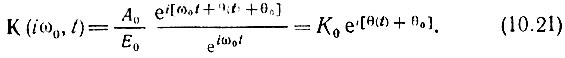
Четырехполюсник с подобной передаточной функцией можно трактовать как линию задержки τ(t), отвечающую условию ω₀τ(t) = θ(t) + θ₀. Отсюда следует, что для осуществления фазовой модуляции требуется линейная цепь с задержкой τ(t), изменяющейся во времени по закону

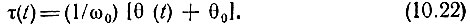
Так как задержка в физической цепи не может быть отрицательной, то слагаемое θ₀/ω₀ = τ₀ имеющее смысл постоянной задержки (в отсутствие модуляции) должно быть не меньше чем (1/ω₀) |θ(t)|_макс.

Реализация линии задержки, допускающей электронное управление величиной τ(t), является непростой задачей. Удачное ее решение получается для диапазона СВЧ при использовании электронных приборов типа лампы бегущей волны, в которых пролетное время можно изменять в некоторых пределах, изменяя потенциал на соответствующих электродах лампы. При заданной и неизменной частоте возбуждения на входе лампы ω₀ изменение пролетного времени на величину Δτ эквивалентно изменению фазы выходного колебания на угол θ(t) = ω₀Δτ. Таким образом, удается получить весьма большие значения θ(t), измеряемые десятками и более радиан.

В диапазоне метровых и более длинных волн наибольшее распространение получили способы, основанные на изменении резонансной частоты колебательного контура усилителя при неизменной частоте возбуждения ω₀. Один из возможных вариантов такого устройства поясняется рис. 10.4. В этом устройстве резонансная частота контура усилителя модулируется с помощью варикапа.

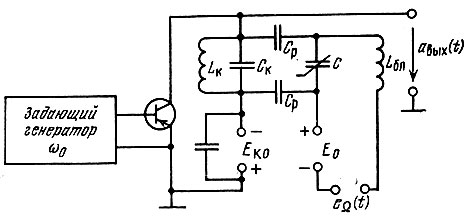
Рис. 10.4. Модуляция фазы колебания изменением резонансной частоты усилителя

Соотношение между вариацией емкости ΔС контура и вариацией Δω его резонансной частоты было установлено в § 9.12. Имеется, однако, принципиальное различие между устройствами, представленными на рис. 9.35 и 10.4. Изменение резонансной частоты контура в автогенераторе (рис. 9.35) равносильно изменению частоты генерируемого колебания. В случае же возбуждения усилителя независимым источником несущего колебания с частотой ω₀ изменение резонансной частоты контура ω_р влияет лишь на фазу выходного колебания. Фазовый сдвиг легко определяется с помощью формулы

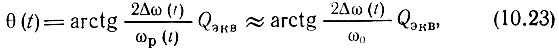
где Δω(t) = ω_р(t) - ω₀. Замена в знаменателе ω_p(t) на ω₀ обычно допустима из-за малости относительного изменения резонансной частоты ω_р при модуляции.

Из выражения (10.23) очевиден основной недостаток рассматриваемого способа осуществления фазовой модуляции: невозможность получения значительного индекса модуляции. Действительно, для обеспечения линейной фазовой модуляции, в данном случае линейной зависимости между θ(t) и Δω(t), аргумент 2Δω(t) Q_экв/ω₀ не должен превышать ~0,5 рад. Это означает, что и амплитуда изменения фазы θ_макс = m ограничена величиной ~0,5 рад. При больших значениях m не только искажается закон модуляции фазы, но и возникает паразитная амплитудная модуляция из-за неравномерности АЧХ резонансного усилителя при значительной расстройке. Однако большим достоинством рассматриваемого способа модуляции является возможность обеспечения высокой стабильности несущей частоты ω₀. Задающий генератор, работающий на фиксированной частоте, можно стабилизировать, например, с помощью кварца.