10.2. Прохождение колебаний через линейные цепи с переменными параметрами. Передаточная функция

В гл. 6, 7 рассматривалась передача различных колебаний через линейные цепи с постоянными параметрами. Связь между входным и выходным колебаниями в таких цепях определялась с помощью передаточной функции К(iω) (спектральный метод) или с помощью импульсной характеристики g(t) (метод интеграла наложения).

Теперь нам предстоит рассмотреть более общую задачу, когда один или несколько элементов линейного четырехполюсника являются функциями времени. Очевидно, что в подобных цепях характер зависимости между входным и выходным сигналами в процессе передачи изменяется. Это означает, что передаточная функция цепи зависит не только от ω, но и от времени; импульсная характеристика также зависит от двух переменных: от интервала а = t - х между моментом приложения единичного импульса х и моментом наблюдения выходного сигнала t (как и для цепи с постоянными параметрами) и, кроме того, от положения интервала а на оси времени. Поэтому для цепи с переменными параметрами импульсную характеристику следует записывать в общей форме: g(t, а) или g(t, x).

Можно сказать, что g(t, а) определяет величину отклика в момент t на единичный импульс, подаваемый на вход цепи в момент х = t - а. Этот импульс записывается в виде дельта-функции δ(t - х).

Если на входе четырехполюсника с импульсной характеристикой g(t, х) действует произвольный сигнал s(t) (рис. 10.2), то, основываясь на принципе суперпозиции, выходной сигнал по аналогии с выражением (6.17) можно определить с помощью выражения

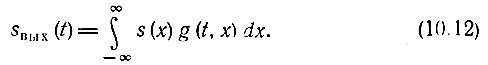
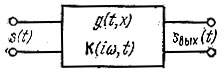
Рис. 10.2. Параметрический четырехполюсник

Переходя к переменной а в соответствии с соотношением х = t - a, получаем

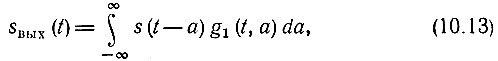
где g₁(t, а) = g(t, t-а).

Для физически осуществимой цепи g₁(t, а) = 0 при а = t - x < 0, т. е. при х > t (см. § 6.3).

Постараемся теперь ввести передаточную функцию K(iω, t), аналогичную функции K(iω) для цепи с постоянными параметрами, но с учетом изменения параметров во времени. Для этого представим функцию s(t - a) в виде интеграла Фурье

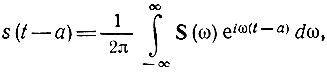
где S(ω) - спектральная плотность сигнала s(t).

Тогда выражение (10.13) переходит в следующее:

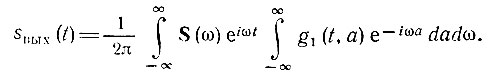
Обозначив внутренний интеграл через K(iω, t), перепишем последнее выражение следующим образом:

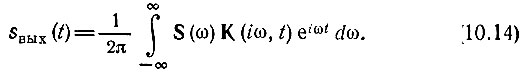
Это выражение совпадает по форме с аналогичным выражением (6.2) для цепи с постоянными параметрами. Отсюда следует, что функцию K(iω, t), определяемую выражением

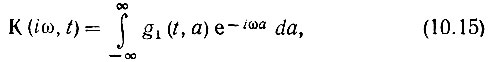
можно рассматривать как передаточную функцию линейной цепи с переменными параметрами.

Как и для цепи с постоянными параметрами, K(iω, t) является преобразованием Фурье от импульсной характеристики g₁(t, а). Так как при а < 0 g₁(t, а) = 0, нижний предел интеграла в (10.15) можно заменить нулем.

Наряду с выражением (10.15) можно получить еще одно определение передаточной функции, в котором импульсная характеристика g₁(t, а) не фигурирует. Для этого используем выражение (10.14) для случая, когда входной сигнал является гармоническим колебанием s(t) = cos ω₀t. Перейдем к аналитическому сигналу z(t) = е^iω₀t, соответствующему заданному сигналу s(t).

Спектральная плотность этого сигнала Z(iω) = 2πδ(ω - ω₀) [см. выражения (2.98) и (3.90)]. Подставляя Z(iω) вместо S(ω) в формулу (10.14), получаем

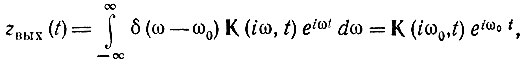
откуда, опуская индекс нуль при ω, получаем

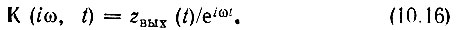
Здесь z_вых(t) - аналитический сигнал, соответствующий выходному сигналу s_вых(t). Таким образом,

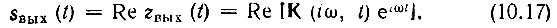
Если передаточная функция К(iω, t) изменяется во времени по периодическому закону с основной частотой Q, то ее можно представить в виде ряда Фурье

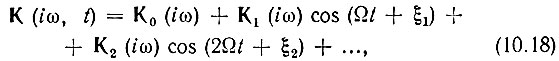
где К₀(iω), К(iω), ... - не зависящие от времени коэффициенты, в общем случае комплексные, которые можно истолковать как передаточные функции некоторых четырехполюсников с постоянными параметрами. Произведение К₀(iω) × cos (nΩt + ξ_n) можно рассматривать как передаточную функцию каскадного соединения двух четырехполюсников: одного с передаточной функцией К_n(iω), не зависящей от времени, и второго с передаточной функцией cos (nΩt + ξ_n), изменяющейся во времени, но не зависящей от частоты ω входного сигнала.

Основываясь на выражении (10.18), любую параметрическую цепь с периодически изменяющимися параметрами можно представить в виде эквивалентной схемы, изображенной на рис. 10.3. В соответствии с (10.16) сигнал (комплексный) на выходе будет

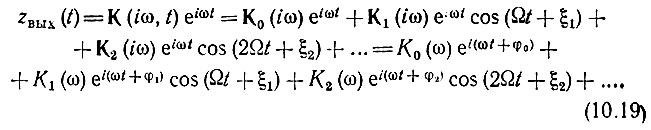
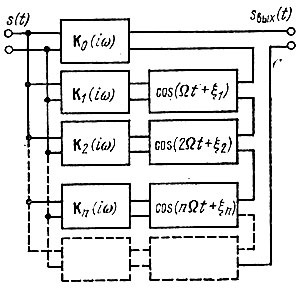
Рис. 10.3. Схема замещения линейной цепи при периодическом изменении параметров

Здесь φ₀, φ₁, φ₂, ... - фазовые характеристики четырехполюсников К₀(iω), К₁(iω), К₂(iω), ...

Переходя к вещественному сигналу на выходе, получаем

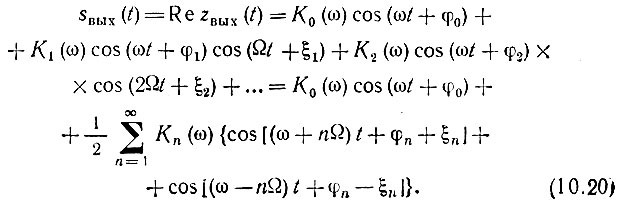
Этот результат указывает на следующее свойство цепи с переменными параметрами: при изменении передаточной функции по любому сложному, но периодическому закону с основной частотой Ω гармонический входной сигнал с частотой со образует на выходе цепи спектр, содержащий частоты ω, ω ± Ω, ω ± 2Ω и т. д.

Если на вход цепи подается сложный сигнал, то все сказанное выше относится к каждой из частот со входного спектра. Само собой разумеется, что в линейной параметрической цепи никакого взаимодействия между отдельными компонентами входного спектра не существует (принцип суперпозиции), и на выходе цепи не возникает частот вида nω₁ ± mω₂, где ω₁ и ω₂ - различные частоты входного сигнала.