Глава 10. Цепи с переменными параметрами

10.1. Общие характеристики цепей с переменными параметрами

Электрические цепи, в которых хотя бы один из параметров изменяется по какому-либо заданному закону, называются параметрическими. Предполагается, что изменение (модуляция) параметра или параметров осуществляется электронным способом при помощи управляющего колебания.

Приведем простые примеры электронных способов осуществления вариации параметров цепи. Рассмотрим зависимость крутизны вольт-амперной характеристики активного элемента i(u) от управляющего колебания е_у(t), наложенного на постоянное напряжение Е₀ (рис. 10.1). Эту зависимость можно записать в виде

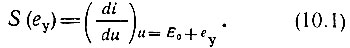
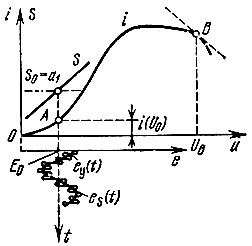
Рис. 10.1. Управление крутизной характеристики

Выражение (10.1) определяет дифференциальную крутизну характеристики в точке Е₀ + е_у. Если в пределах изменения е_у характеристику можно аппроксимировать полиномом второй степени i = i(Е₀) + а₁u + а₂u², то выражение (10.1) приводится к виду

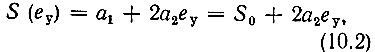
где S₀ = а₁ - дифференциальная крутизна в точке А (рис. 10.1). Зависимость крутизны от управляющего напряжения изображена на рис. 10.1 в виде наклонной прямой линии.

Пусть е_у = Е_у cos ω_уt. Тогда крутизну можно записать в виде функции времени

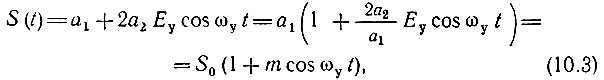
где m = 2a₂E_у/a₁ - глубина "модуляции" параметра S. Соответствующим выбором Е₀ и Е_у можно обеспечить условие m < 1.

По отношению к слабому сигналу e_s(t), наложенному на управляющее напряжение e_у(t), рассматриваемое устройство можно трактовать как линейное, с переменным параметром S(t), управляемым по закону (10.3). Существенной особенностью дифференциальной крутизны (а также дифференциального сопротивления) является то, что этот параметр может принимать отрицательное значение. Для этого нужно, чтобы вольт-амперная характеристика на некотором участке имела отрицательный наклон (окрестность точки В на рис. 10.1).

Аналогичным образом можно истолковать принцип электронного управления емкостью. Пусть к нелинейной емкости приложены два колебания: одно сильное, которое назовем управляющим, а второе слабое - сигнальное. Воспользуемся аппроксимацией вольт-кулонной характеристики, представленной на рис. 8.2, полиномом второй степени

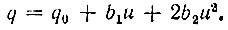
Тогда дифференциальную емкость по аналогии с (10.2) можно определить выражением

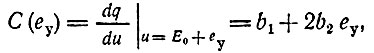
где b₁ = С₀ - дифференциальная емкость в точке u = Е₀.

Если управляющее напряжение является гармоническим колебанием е_у = Е_у cos ω_уt, то можно написать

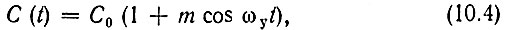
где m = 2b₂E_у/b₁ - глубина модуляции емкости.

После такого преобразования можно говорить о воздействии одного лишь сигнала е_s(t) на периодически изменяющуюся во времени емкость С(t), так как влияние управляющего колебания учтено заменой нелинейной емкости линейной параметрической емкостью.

При использовании в качестве управляемого элемента барьерной емкости p-n-перехода можно исходить из выражения

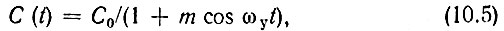
где m = Е_у/2 (е_к + E₀); е_к - контактная разность потенциалов, зависящая от кристалла, примесей и т. д.

Аналогичные выражения можно составить и для параметрической индуктивности L(t) управляемой током.

При установлении соотношений между зарядом, током и напряжением на параметрической емкости следует исходить из очевидных выражений

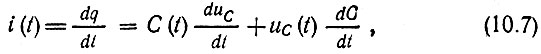
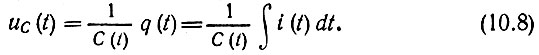
Для параметрической индуктивности L(t) имеют место следующие соотношения, связывающие потокосцепление Φ, напряжение u_L и ток i:

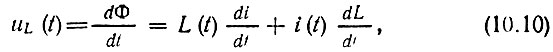
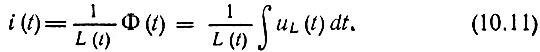
Следует отметить принципиальное отличие реактивных элементов от резистивных: дифференциальные емкость и индуктивность не могут быть отрицательными^*. Физически это объясняется тем, что увеличение напряжения на емкости не может вызывать уменьшение зарядов, а увеличение тока через индуктивность не может приводить к уменьшению потокосцепления. Иными словами, энергия, запасаемая в электрическом поле конденсатора или в магнитном поле катушки, не может быть отрицательной.

^* (Имеются в виду обычные элементы. С помощью же усилительных схем с обратной связью можно имитировать отрицательные C и L.)

В дальнейшем изложении элементы с изменяющимися во времени параметрами R(t), С(t) и L(t) будут рассматриваться как линейные элементы; к ним применим принцип суперпозиции. Термины "дифференциальное" сопротивление, "дифференциальные" емкость или индуктивность, существенные Для характеристики способов вариации параметров, но не для анализа составленных из этих параметров цепей, не будут применяться.

Цепи с переменными параметрами играют очень большую роль в радиотехнике и электронике.

Можно говорить о двух принципиально различных видах изменения параметров:

1) умышленное, управляемое изменение для осуществления различных преобразований сигналов (модуляция, преобразование частоты, параметрическое усиление и т. д.);

2) неуправляемое изменение, обусловленное различными физическими явлениями при передаче сигналов в свободном пространстве, например изменяющейся во времени задержкой сигнала, колебанием величины затухания волн при их распространении, изменением фазовых соотношений при многолучевом распространении радиоволн, изменением сигналов во времени из-за флуктуации параметров тракта и т. д.

Влияние изменений параметров второго вида, носящих обычно статистический характер, будет рассмотрено в гл. 11. В настоящей главе изучаются явления при принудительном изменении во времени одного из параметров линейной цепи (апериодической или колебательной). В основном имеется в виду изменение параметра по гармоническому закону.