11.2. Преобразование нормального процесса в безынерционных нелинейных цепях

Реальное нелинейное устройство представляет собой сочетание нелинейных безынерционных элементов с линейными инерционными электрическими цепями. Это очень усложняет нахождение статистических характеристик сигнала и шума на выходе всего устройства. Для линейных цепей просто определить корреляционную (или спектральную) функцию, но очень сложно - закон распределения. В нелинейных же, но безынерционных элементах, наоборот, основная трудность состоит в нахождении корреляционной функции. Поэтому общих методов анализа преобразования случайных процессов в нелинейных устройствах не существует. Приходится ограничиваться некоторыми частными задачами, представляющими практический интерес и поддающимися решению, а также прибегать к различным идеализациям характеристик изучаемой модели устройства.

Пусть на нелинейный элемент действует случайное колебание (напряжение, ток) с заданной плотностью вероятности р(х). Требуется найти плотность вероятности р(y) выходной величины y. Связь между y и х определяется нелинейной зависимостью y = f(x), имеющей смысл, например, вольт-амперной характеристики электронного, полупроводникового или иного активного элемента.

Если f(x) определяет однозначное соответствие между х и y в каждый рассматриваемый момент, независимо от значений х в предыдущие моменты времени (безынерционный элемент), то плотность вероятности р(y) находится из очевидного соотношения

откуда с учетом неотрицательности р(х) и р(y)

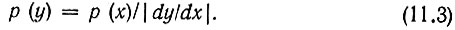
Если обратная функция х = φ(y) неоднозначна, то

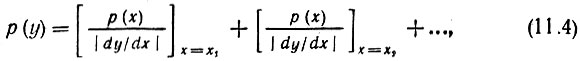
где x₁, x₂, ... - значения входной величины x, соответствующие рассматриваемому значению y.

Если характеристика y = f(х) постоянна на некотором интервале изменения х, то выражение (11.3) следует дополнить слагаемым с дельта-функцией, учитывающим интегральную вероятность пребывания х ниже (или выше) определенного уровня.

Нахождение р(y) проще всего пояснить на практических примерах.

1. Воздействие нормально распределенного случайного процесса х(t) на элемент с симметричной квадратичной характеристикой (рис. 11.1). Показанную на рис. 11.1 вольт-амперную характеристику можно реализовать, например, с помощью двухтактного включения двух диодов, обладающих вблизи нуля квадратичными характеристиками (рис. 11.2).

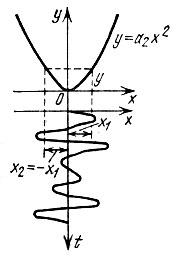
Рис. 11.1. Воздействие случайного процесса на нелинейный элемент с квадратичной характеристикой

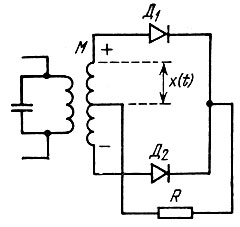
Рис. 11.2. Двухтактное включение диодов

При полярности напряжения, обозначенной на рис. 11.2, ток, равный а₂х², проходит через диод Д₁, при противоположной полярности - через диод Д₂.

Полагая 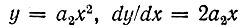и учитывая, что какому-либо фиксированному значению y соответствуют два значения х, а именно 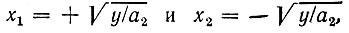по формуле (11.4) находим

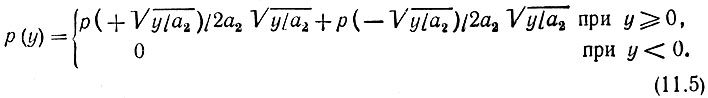
Подставляя 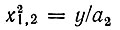в выражение для плотности вероятности р(х):

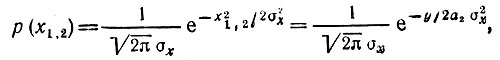
получаем окончательно

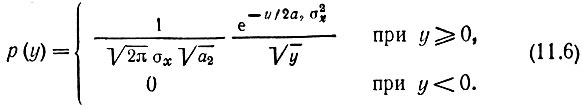
График этого распределения изображен на рис. 11.3 (при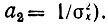

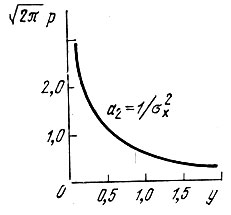
Рис. 11.3. Плотность вероятности тока в цепи с квадратичной вольт-амперной характеристикой при воздействии нормального случайного процесса

2. Воздействие нормально распределенного процесса на однополупериодный детектор с линейно ломаной характеристикой (рис. 11.4).

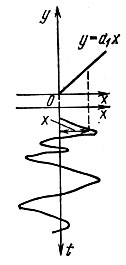
Рис. 11.4. Воздействие случайной функции на однополупериодный детектор

В данном случае

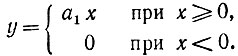
Очевидно, что в соответствии с (11.3)

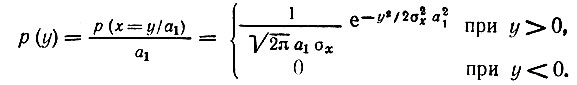
Особое внимание следует обратить на поведение функции р(y) в точке y = 0. Так как y = 0 при любых отрицательных значениях то вероятность Р(y = 0) равна вероятности того, что х ≤ 0. Но вероятность Р(х ≤ 0) = 1/2. Отсюда вытекает, что плотность вероятности р(y = 0) = ∞.

Это обстоятельство можно учесть, записав выражение для р(y) в форме

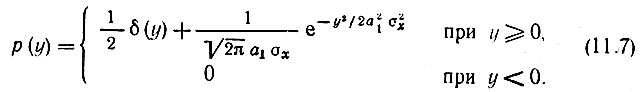
Слагаемое ¹/₂δ(y) равно нулю всюду, кроме точки y = 0, где оно обращается в бесконечность. При интегрировании же по y это слагаемое дает 1/2. Графики р(х) к р(y) изображены на рис. 11.5.

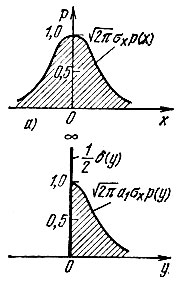
Рис. 11.5. Плотность вероятности случайного процесса на входе (а) и выходе (б) однополупериодного детектора

3. Воздействие нормально распределенного процесса на ограничитель (рис. 11.6).

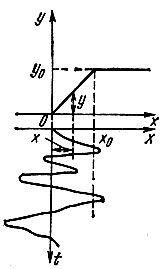
Рис. 11.6. Воздействие случайной функции на ограничитель

По аналогии с предыдущим случаем нетрудно составить выражение

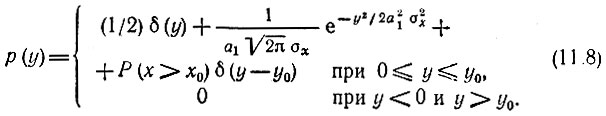
Графики распределения х и у изображены на рис. 11.7. Приведенных примеров достаточно для уяснения метода нахождения плотности вероятности случайной величины на выходе нелинейного безынерционного элемента с любой вольт-амперной характеристикой. Простота этого метода обусловлена тем, что не учитывается влияние выходных цепей (инерционных) на работу рассматриваемого нелинейного элемента.

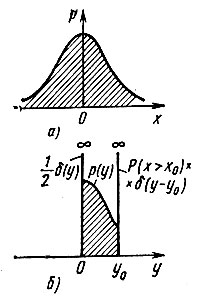
Рис. 11.7. Плотность вероятности случайного процесса на входе (а) и выходе (б) ограничителя