11.3. Преобразование энергетического спектра в безынерционном нелинейном элементе

Прямое определение энергетического спектра выходного процесса по известному спектру на входе нелинейного элемента не представляется возможным. Единственный путь - это определение корреляционной функции с последующим применением преобразования Фурье.

Если на входе нелинейного элемента с характеристикой y = f(х) действует стационарный процесс х(t), то корреляционная функция на выходе может быть представлена в форме

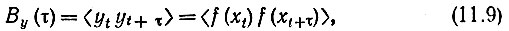
где x_t и x_t+τ - значения х(t) в моменты времени t и t + τ; y_t и y_t+τ - соответствующие им значения y на выходе нелинейного элемента.

Для усреднения произведения f(x_t) f(x_t+τ) должна быть известна двумерная плотность вероятности входного процесса р(x_t, x_t+τ). Если эта плотность вероятности известна, то корреляционную функцию B_y(_τ) можно представить в виде следующего выражения:

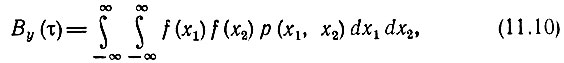
где для удобства записи через х₁ и х₂ обозначены соответственно х_t, x_t+τ.

Этот интеграл удается вычислить далеко не во всех практически важных задачах. В связи с этим часто приходится прибегать к различным обходным способам, один из которых будет приведен далее.

В качестве примера задачи, достаточна интересной для практики и доступной для решения прямым методом, рассмотрим воздействие стационарного нормального процесса х(t) на нелинейный элемент с квадратичной характеристикой y = а₂x² (см. пример 1 предыдущего параграфа).

Двумерная плотность вероятности процесса х(t) равна^*

^* (См., например, [1].)

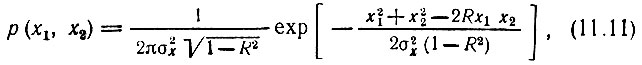
где R - коэффициент корреляции величин х₁ и х₂, т. е. R = R_x(τ).

Подставив выражение (11.11), а также f(х) = а₂х² в (11.10), получим

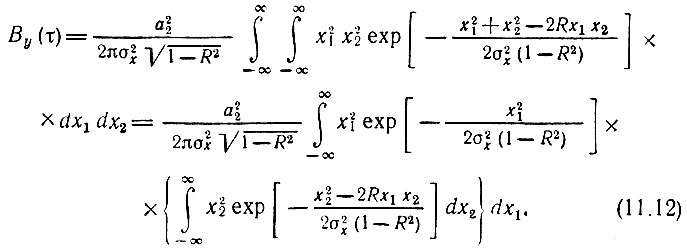
Интеграл в фигурных скобках легко вычислить, дополнив выражение х₂² - 2Rх₁х₂ до квадрата разности х₂² - 2Rх₁х₂ = (х₂ - - Rх₁)² - R²х₁² и заменив переменную х₂ - Rx₁ = z:

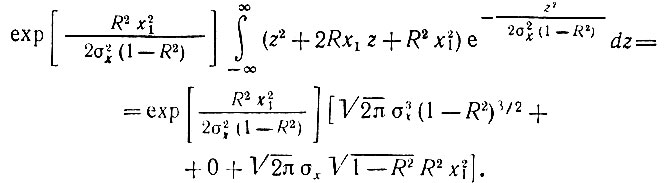
Подставляя этот результат в (11.12), получаем

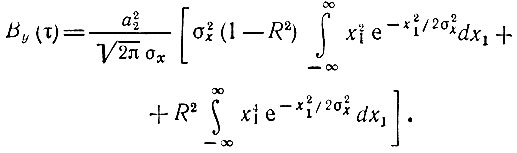
Далее определяем

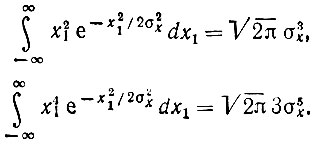
Таким образом,

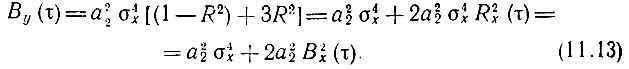
Здесь использовано известное соотношение 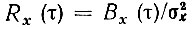(при

Пр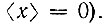едставляя корреляционную функцию узкополосного процесса в форме (4.76) и учитывая, что

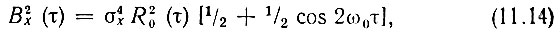
где R₀ - огибающая корреляционной функции узкополосного процесса, записываем выражение (11.13) в окончательном виде

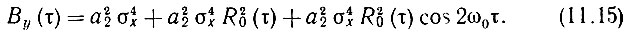
Применяя затем преобразование Фурье, получаем общее выражение для энергетического спектра процесса на выходе квадратичного элемента (при нормальном процессе на входе):

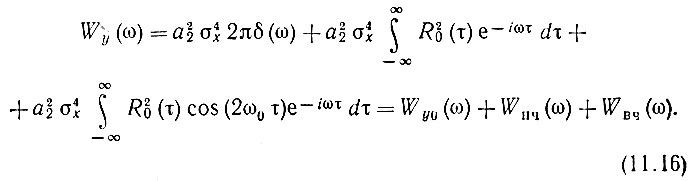
Первое слагаемое (дискретное) соответствует постоянной составляющей выходного колебания, второе - низкочастотной флуктуационной составляющей (спектр которой примыкает к нулевой частоте) и третье - высокочастотной флуктуационной составляющей со спектром, группирующимся вблизи частоты 2ω₀.