11.4. Воздействие узкополосного шума на амплитудный детектор

Амплитудный детектор, содержащий диод и фильтр нижних частот (RС-цепь), представляет собой сочетание безынерционного нелинейного элемента с инерционной линейной цепью.

Расчленим рассматриваемое устройство на две самостоятельные части: 1) нелинейный элемент, 2) фильтр нижних частот.

Изложенные в предыдущих параграфах методы, а также некоторые другие специальные приемы позволяют в принципе найти закон распределения и корреляционную функцию шума сначала на выходе нелинейного элемента (диода), а затем и на выходе фильтра. В общем случае эти исследования требуют весьма громоздких вычислений. Задачу можно значительно облегчить, если использовать некоторые упрощения, вытекающие из принципа работы реальных устройств.

Рассмотрим сначала "линейное" детектирование, т. е. детектирование высокочастотного колебания с достаточно большими амплитудами. В данном случае под таким колебанием подразумевается нормальный шум (в отсутствие сигнала), сформированный избирательными цепями на входе детектора. Как и при детектировании полезного амплитудно-модулированного колебания можно считать, что напряжение на выходе линейного детектора воспроизводит огибающую амплитуд высокочастотного колебания, в данном случае огибающую шума. Поэтому при линейном детектировании нет необходимости рассматривать отдельно статистические характеристики тока диода и напряжения на выходе RС-цепи. Напряжение u_вых(t), развиваемое на этой цепи, можно приравнять огибающей шума на входе детектора U(t) (т. е. считать, что коэффициент передачи детектора равен единице). При таком подходе статистические характеристики шума на выходе детектора полностью совпадают с приведенными в § 4.6 характеристиками огибающей A(t). Таким образом, приходим к выводу, что напряжение шума на выходе линейного детектора обладает релеевским распределением:

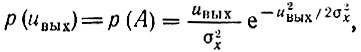
По формулам (4.71)-(4.72) находим:

- среднее значение (постоянная составляющая) шумового напряжения

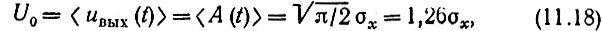
- средний квадрат напряжения

Отсюда следует, что дисперсия шума на выходе линейного детектора

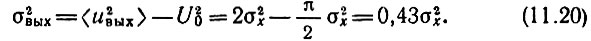
Итак, основные параметры шума на выходе - постоянная составляющая U₀ и дисперсия σ²_вых - просто выражаются через дисперсию σ²_х высокочастотного шума, действующего на входе детектора.

Корреляционную функцию и энергетический спектр выходного шума нетрудно вычислить по формулам (4.77), (4.78).

В качестве примера рассмотрим воздействие на линейный детектор нормального шума х(t), энергетический спектр которого W_x(ω) определяется выражением

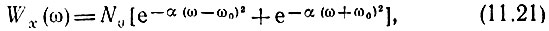
а корреляционная функция в соответствии с (4.39) и с учетом [6] (формулы (3.896.3) и (3.896.4)

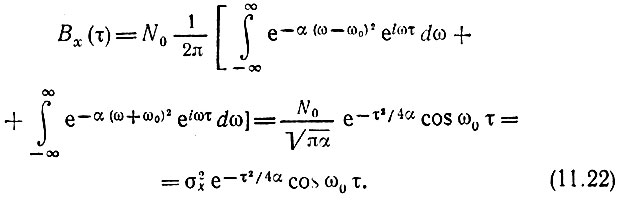
Тогда

и в соответствии с (4.78)

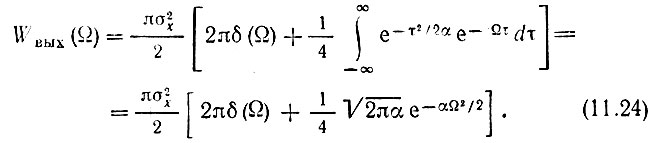
Слагаемое с дельта-функцией соответствует постоянной составляющей напряжения на выходе детектора.

График W_вых(Ω) изображен на рис. 11.8, б. Ширина этого спектра в 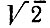раз больше ширины спектра W_x(ω) на входе детектора (рис. 11.8, а).

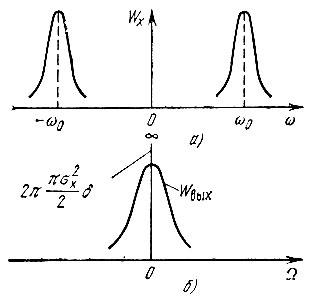
Рис. 11.8. Энергетический спектр случайного процесса на входе (а) и выходе (б) амплитудного детектора

Линейный амплитудный детектор воспроизводит огибающую узкополосного колебания, независимо от особенностей структуры его спектра. Полученный результат свидетельствует о том, что огибающая каждой из реализаций рассматриваемого шума (на входе детектора) обладает спектром более широким, чем частотная полоса самой реализации. На первый взгляд это может показаться странным, поскольку известно, что для модулированного колебания ширина спектра огибающей либо совпадает со спектром самого колебания (при AM), либо уже его (при ЧМ). Это кажущееся противоречие легко устраняется, если принять во внимание полную корреляцию между колебаниями нижних и верхних боковых частот при модуляции. Достаточно нарушить, например, симметрию амплитуд или фаз боковых частот при амплитудной модуляции, чтобы сумма трех колебаний с частотами ω₀, ω₀ + Ω и ω₀ - Ω представляла собой колебание, огибающая которого содержит помимо частоты Ω еще и частоты 2Ω, 3Ω и т. д. В этом случае амплитудный детектор выделит на выходе колебание, спектр которого будет шире, чем частотная полоса высокочастотного колебания на входе. В спектре же шума нет никакой корреляции (и тем более симметрии) между спектральными составляющими, частоты которых расположены слева и справа от центральной частоты ω₀. Естественно, что огибающая каждой из реализаций шума обладает спектром более широким, чем модулированное колебание с той же шириной спектра. Соответственно увеличивается и средняя ширина спектра огибающей шума, т. е. энергетический спектр огибающей.

Рассмотрим теперь воздействие нормального шума на квадратичный детектор. В данном случае напряжение на выходе детектора с учетом отфильтровывания высокочастотной составляющей шума по аналогии с выражением (8.55) можно представить в форме

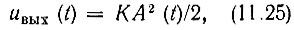
где К - коэффициент, учитывающий параметр вольт-амперной характеристики диода а₂ и величину сопротивления нагрузки на выходе детектора.

Применяя формулу (11.3), в которой под р(х) следует подразумевать плотность вероятности огибающей А(t), находим закон распределения шумового напряжения на выходе квадратичного детектора:

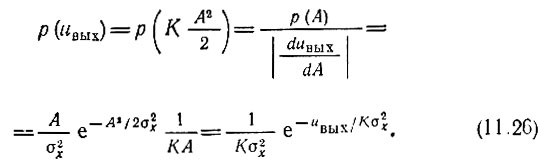
Итак, при воздействии на квадратичный детектор с фильтром нижних частот узкополосного нормального процесса шум на выходе всего устройства имеет экспоненциальное распределение.

Вычислим постоянную составляющую выходного напряжения

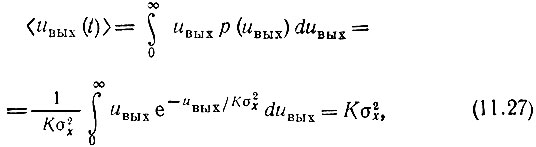
а также средний квадрат напряжения

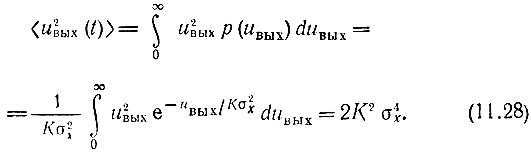
Отсюда следует, что дисперсия шума на выходе

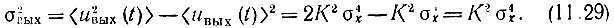
Для полного описания свойств шума на выходе квадратичного детектора остается вычислить его корреляционную функцию и энергетический спектр. Это можно выполнить с помощью формул (11.15), (11.16). Второе слагаемое в выражении (11.15) определяет искомую корреляционную функцию, а второе слагаемое в выражении (11.16) - соответствующий этой функции энергетический спектр.

При 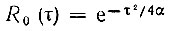(см. предыдущий пример) получаем

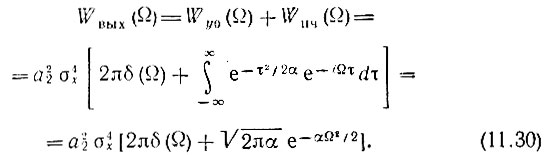
Графики функций W_x(ω) и W_вых(Ω) по форме совпадают с графиками на рис. 11.8. Они отличаются только масштабом по оси ординат из-за различия в постоянных коэффициентах [a²σ⁴_x вместо πσ²_x/2 перед квадратными скобками в (11.24) и единица вместо 1/4 перед вторым слагаемым].