11.5. Совместное воздействие гармонического колебания и нормального шума на амплитудный детектор

При наложении узкополосного шума х(t) = A(t) cos [ω₀t + θ(t)] на сигнал s(t) = Е cos ω₀t суммарное колебание можно записать в форме

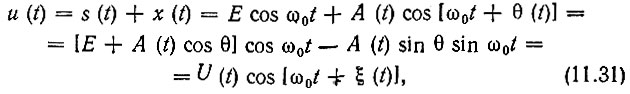
где огибающая U(t) и фаза ξ(t) по аналогии с (8.43) и (8.44) определяется выражениями

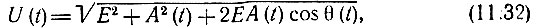
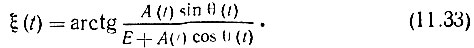
При анализе воздействия колебания на амплитудный детектор статистическими характеристиками фазы ξ(t) можно не интересоваться (этот вопрос будет рассмотрен в следующем параграфе применительно к частотному детектору). Основное значение имеет плотность вероятности р(U) огибающей U, определяемая по формуле [1]

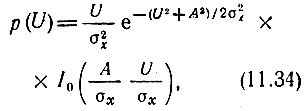
где I₀ - бесселева функция комплексного аргумента (модифицированная).

Определяемая формулой (11.34) функция называется обобщенной функцией Релея. Графики функции р(U) для нескольких значений Е/σ_х приведены на рис. 11.9.

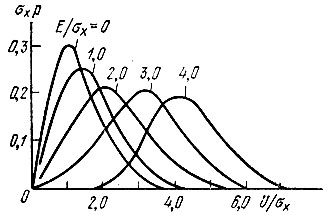
Рис. 11.9. Релеевская плотность вероятности (обобщенная)

При Е/σ_х = 0 (отсутствие сигнала) выражение (11.34) переходит в (4.70). В другом крайнем случае, когда амплитуда сигнала Е очень велика по сравнению с σ_х, кривая р(U) близка к гауссовой кривой с дисперсией σ²_х и средним значением, равным Е.

Рассмотрим сначала линейное детектирование. Будем считать, что напряжение на выходе детектора совпадает с огибающей амплитуд высокочастотного напряжения на входе. Тогда, основываясь на формуле (11.34), находим постоянную составляющую напряжения на выходе детектора

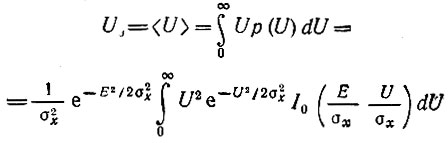
и средний квадрат напряжения

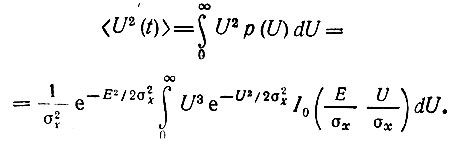
После вычисления интегралов [5] получаем следующие выражения:

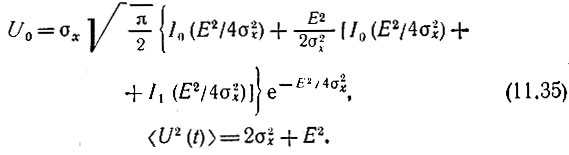
Следовательно, дисперсия

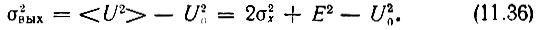
Так как в отсутствие сигнала (при Е = 0) постоянная составляющая в соответствии с (11.35) и (11.18) равна 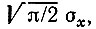то обусловленное сигналом приращение постоянной составляющей будет 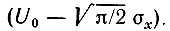Следовательно, отношение мощности сигнала к мощности помехи на выходе линейного детектора

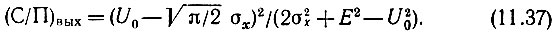
Рассмотрим предельные случаи, когда (Е²/2σ²_х) << 1 (слабый сигнал) и (Е²/2σ²_х) >> 1 (сильный сигнал). При слабом сигнале, отбросив степени (Е²/2σ²_х) выше первой, которые получаются при асимптотическом представлении функций I₀ (Е²/4σ²_х) и I₁ (Е²/4σ²_х), выражение (11.35) можно записать в укороченном виде

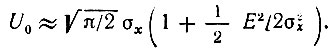
При этом приращение постоянной составляющей

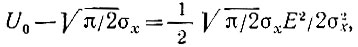
а дисперсия

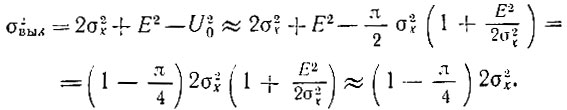
Таким образом, отношение сигнал-помеха

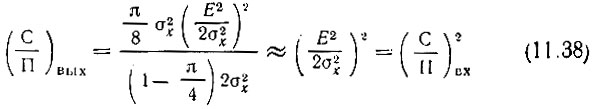
при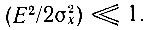

При сильном сигнале приближенные выражения функций Бесселя от больших аргументов позволяют представить выражение (11.35) в виде

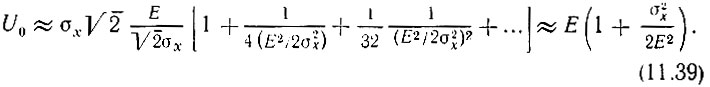
Подставляя это значение U₀ в формулу (11.37), получаем

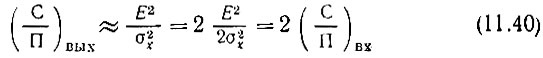
при

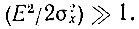
Проведем аналогичное рассмотрение для квадратичного детектирования.

Заменяя в формуле (11.25) A(t) на U(t), получаем напряжение на выходе квадратичного детектора

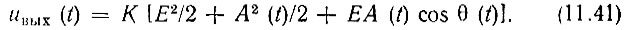
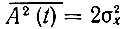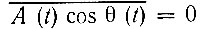Усредняя это выражение по времени и учитывая, что и {как и среднее значение 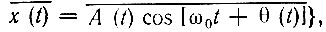получаем постоянную составляющую напряжения на выходе квадратичного детектора

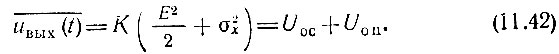
Слагаемое U_оп = Кσ²_х определяет постоянную составляющую, обусловленную помехой [см. выражение (11.27)] в отсутствие сигнала. Слагаемое же. U_oc = КЕ²/2, представляющее собой приращение постоянной составляющей под действием гармонического напряжения, можно рассматривать как полезный сигнал на выходе детектора.

Возводя выражение (11.41) в квадрат, получаем

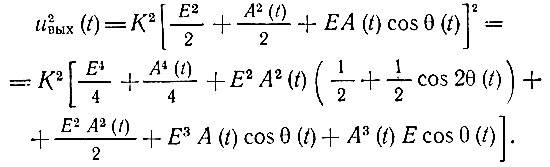
Слагаемые с cos θ(t) и cos 2θ(t) при усреднении обращаются в нуль. Поэтому средняя мощность на выходе^*

^* (При усреднении А⁴(t) получается

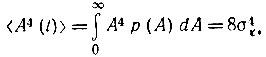
Ввиду эргодичности рассматриваемого процесса в данном параграфе не делается различия между усреднением по множеству и по времени.)

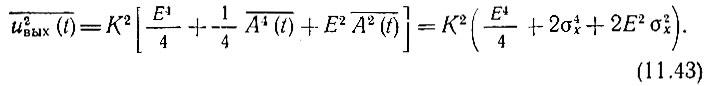
Вычитая из этого выражения 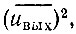находим дисперсию шума на выходе квадратичного детектора

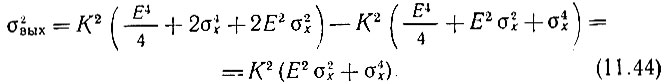
При Е = 0 это выражение переходит в (11.29). Составим теперь отношение сигнал-помеха на выходе детектора (по мощности)

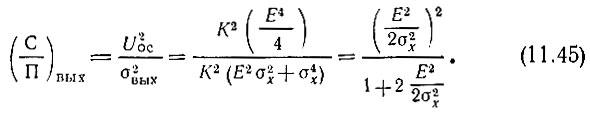
Но Е²/2σ²_х есть отношение сигнал-помеха (по мощности) на входе детектора. Таким образом, при значениях 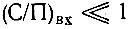(т. е. при

а при больших значениях (С/П)_вх, т. е. при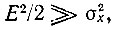

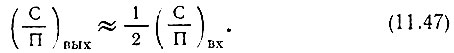
Так, например, при Е²/2σ²_х = 1/10 отношение (С/П)_вых = 1/120 [формула (11.45)], а при Е²/2σ²_х ≥ 4 отношение (С/П)_вых близко к половине отношения сигнала к помехе на входе.

На основании формулы (11.45) можно сделать следующее важное заключение: при слабом (относительно помехи) сигнале в квадратичном детекторе имеет место подавление сигнала, а при сильном сигнале отношение (С/П)_вых пропорционально отношению сигнала к помехе на входе.

Сопоставим полученные результаты для квадратичного и линейного детектирования. Сравнение формул (11.46) и (11.38) показывает, что при слабом сигнале и сильной помехе линейный и квадратичный детекторы ведут себя одинаково: отношение сигнал-помеха на выходе пропорционально квадрату отношения сигнал-помеха на входе. Таким образом, и в линейном детекторе имеет место подавление слабого сигнала. Анализ показывает, что это свойство присуще детекторам и с любыми другими вольт-амперными характеристиками.

С другой стороны, при Е >> σ_х отношение сигнал-помеха на выходе квадратичного детектора в четыре раза (по мощности) меньше, чем у линейного [ср. формулы (11.47) и (11.40)]. Это объясняется тем, что при квадратичном детектировании сильный сигнал выносит помеху на участок характеристики с повышенной крутизной, что приводит к относительному увеличению помехи. Действительно, пусть огибающая гармонического колебания на входе, равная 1 В, получила приращение а << 1. Тогда напряжение на выходе квадратичного детектора в соответствии с (11.25) увеличится от K/2 до (К/2) (1 + а)² ≈ (К/2)(1 + 2а), т. е. относительное приращение будет 2а, а при линейном детектировании это приращение будет всего лишь а. Переходя от напряжения к мощности, получим проигрыш в четыре раза.

Хотя проведенное рассмотрение относится к гармоническому (немодулированному) сигналу, полученные выводы можно полностью распространить на обработку прямоугольных импульсных радиосигналов на фоне помех, когда импульс на выходе детектора есть приращение постоянной составляющей выпрямленного напряжения в промежутке времени, равном длительности импульса.

Наличие амплитудной модуляции сигнала, которую можно рассматривать как медленное изменение постоянной составляющей напряжения на выходе детектора, также не оказывает существенного влияния на сравнительную оценку квадратичного и линейного детектирования.

Следует, наконец, отметить, что все полученные в этом параграфе результаты не зависят от соотношения между несущей частотой сигнала ω₀ и мгновенной частотой помехи ω₀ + θ. Из этого следует, что наложение частотной или фазовой модуляции на сигнал (при постоянной амплитуде) не оказывает влияния на отношение сигнал-помеха на выходе детектора. Это положение согласуется с основными свойствами амплитудного детектора, установленными в гл. 8.