11.6. Совместное воздействие гармонического колебания и нормального шума на частотный детектор

Основываясь на рассмотренном в § 8.9 принципе работы частотного детектора, в дальнейшем будем исходить из структурной схемы, показанной на рис. 11.10. Сигнал s(t) на входе амплитудного ограничителя представляет собой частотно-модулированное колебание (имеется в виду тональная модуляция частоты)

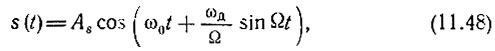
а помеха - случайный нормальный процесс с энергетическим спектром W_x(ω) = W₀, равномерным в полосе пропускания фильтра промежуточной частоты (имеется в виду супергетеродинный приемник).

Рис. 11.10. Структурная схема частотного детектора

Полосу пропускания этого фильтра 2Δω₀ можно приравнять удвоенной девиации частоты, т. е. Δω₀ = ω_д. Фильтр нижних частот на выходе детектора должен обладать полосой прозрачности от 0 до Ω_макс, где Ω_макс - наивысшая частота модуляции. Помеху, действующую на входе ограничителя, запишем, как и в предыдущем параграфе, в виде х(t) = A(t) cos [ω₀t + θ(t)].

При анализе совместного действия s(t) и х(t) на частотный детектор облегчим задачу, рассматривая раздельно два режима:

1) при отсутствии полезной частотной модуляции, когда на входе детектора действует чисто гармоническое колебание s(t) = A_s cos ω₀t и шум х(t), 2) при наличии частотной модуляции. Будем считать, что во втором режиме помеха на выходе детектора остается такой же, что и в первом.

Итак, в отсутствие модуляции суммарное колебание на входе ограничителя равно [см. (11.31)]

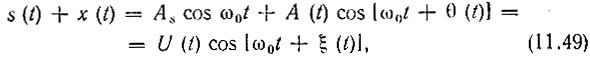
где U(t) и ξ(t) определяются выражениями (11.32) и (11.33).

Обозначив порог ограничения через U_пор, приходим к следующему выражению для колебания на выходе ограничителя:

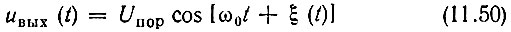
[сравнить с (8.45)].

Напряжение на выходе частотного детектора, пропорциональное производной фазы ξ(t) в отсутствие полезной модуляции, является помехой. Таким образом,

где S_чд - крутизна характеристики частотного детектора (см. § 8.9). Как видим, интенсивность и структура помехи х_вых(t) на выходе частотного детектора полностью определяется статистическими характеристиками производной фазы ξ(t).

Общее выражение для фазы при любых соотношениях между A(t) и A_s(t) имеет вид (11.33). Однако в реальных условиях приема частотно-модулированных колебаний обеспечивается значительное превышение сигнала над помехой. Обычно 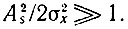(Как и в предыдущем параграфе, σ²_х - средняя мощность шума на входе детектора.) Поэтому выражение (11.33) для фазы можно упростить:

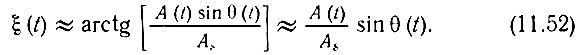
Статистические характеристики случайной функции ξ(t) = (А(t)/A_s) sin θ(t) совпадают с характеристиками, найденными в § 4.6 для квадратурных слагаемых узкополосного процесса. Там было показано, что функция А(t) sin θ(t) обладает нормальным законом распределения и энергетическим спектром 2W_x(ω₀ + Ω) [см. выражение (4.64)]. Таким образом,

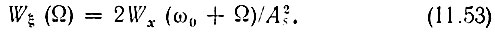
При дифференцировании нормального случайного процесса распределение остается нормальным (см. §7.1). Следовательно, ξ(t), т. е. мгновенное значение частотного отклонения, также обладает нормальным распределением.

Итак, при 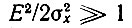шум на выходе частотного детектора (как и на входе) является нормальным случайным процессом.

Остается определить энергетический спектр процесса ξ(t). Для этого достаточно умножить W_ξ(Ω) на Ω² (см. § 7.3). Таким образом,

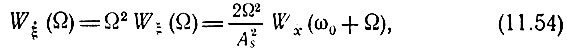
а энергетический спектр помехи на выходе частотного детектора в соответствии с выражением (11.51)

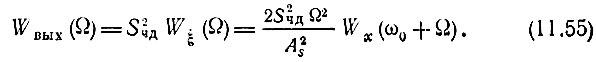
Наконец, корреляционная функция помехи на выходе фильтра нижних частот (с полосой пропускания Ω_макс)

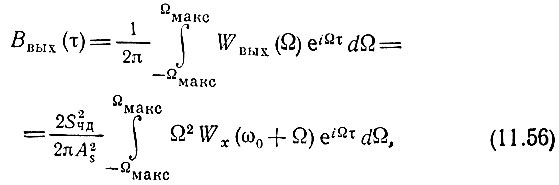
и дисперсия, т. е. средняя мощность помехи,

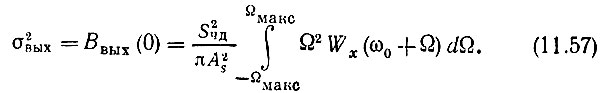
Обратимся теперь к режиму частотной модуляции, при котором напряжение на выходе частотного детектора пропорционально девиации частоты. При тональной модуляции амплитуда напряжения будет

Итак, мощность сигнала на выходе (без учета влияния помехи) равна 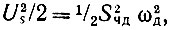а мощность помехи (без учета модуляции) определяется выражением (11.57). Следовательно, отношение сигнал - помеха на выходе

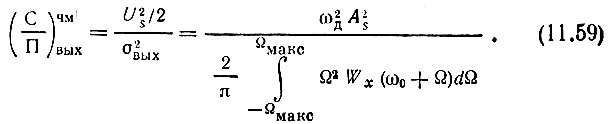
Проиллюстрируем выражение (11.59) следующим примером. Пусть помеха на входе детектора является белым шумом с энергетическим спектром W_x(ω) = W₀ = const.

Тогда интеграл в (11.59) равен 2Ω³_максW₀/3 и выражение (11.59) легко приводится в виду

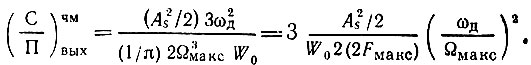
Но A_s²/2 есть мощность сигнала на входе, а W₀2(2F_макс) есть не что иное, как σ²_x, т. е. мощность шума в двух полосах 2Δf₀ = 2F_макc (одна в области ω > 0, вторая в области ω < 0).

Таким образом, окончательно

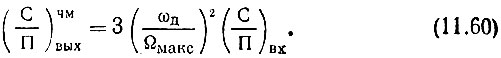
Увеличивая отношение ω_д/Ω_макс, т. е. индекс угловой модуляции, можно получить большой выигрыш в величине сигнал-помеха по сравнению с величиной С/П в системах с амплитудной модуляцией. Подобный способ получил широкое распространение в системах радиовещания на УКВ, а также в каналах звукового сопровождения в телевидении.

Следует подчеркнуть, что преимущества широкополосной частотной модуляции сохраняются, пока помеха на входе детектора слабее сигнала и пока обеспечивается полное ограничение амплитуды колебания на входе детектора. В тех же случаях, когда помеха сильнее сигнала, имеет место подавление сигнала.