11.7. Взаимодействие гармонического колебания и нормального шума в амплитудном ограничителе с резонансной нагрузкой

Как и в § 11.5, представим сумму гармонического колебания s(t) = Е cos ω₀t и узкополосного шума х(t) = А(t) cos [ω₀t + θ(t)] в виде

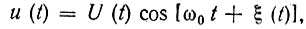
где медленно изменяющиеся функции U(t) (огибающая) и ξ(t) (фаза) определяются выражениями (11.32), (11.33).

Вольт-амперную характеристику нелинейного элемента, осуществляющего амплитудное ограничение, определим выражением

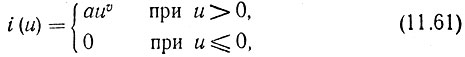
где а - постоянный множитель; υ - положительное действительное число; i и u - нормированные (безразмерные) величины.

Кривые i(u) для υ = 0; 1/2; 1 и 2 изображены на рис. 11.11. Ток i отличен от нуля только при положительных полуволнах входного колебания. Случаи υ = 1; 2 соответствуют однополупериодному выпрямлению (детектированию); υ = 1 соответствует также оптимальному режиму нелинейного резонансного усилителя с углом отсечки θ = 90° (см. § 8.4). Случай υ = 1/2 характерен для того же усилителя при заходе и в область насыщения характеристики, а также для нежесткого ограничения амплитуды. Наконец, случай υ = 0 соответствует идеальному ограничению.

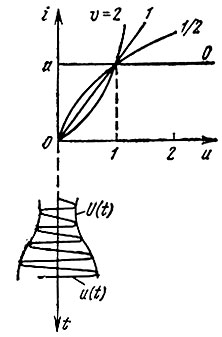
Рис. 11.11. Характеристики нелинейных элементов

Общее выражение для тока имеет вид^*

^* (См. [3], а также предыдущее издание настоящей книги, М., "Сов. радио", 1971.)

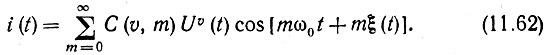
Это выражение определяет ток i(t) в виде суммы колебаний, средние частоты которых mω₀ и фазы mξ(t) кратны частоте ω₀ и фазе ξ(t). Огибающие же этих колебаний U^υ(t) равны υ-й степени амплитуды воздействия. Постоянные коэффициенты С(υ, m) зависят от степени υ, т. е. от формы вольт-амперной характеристики i(u).

Если на выходе устройства имеется фильтр, пропускающий только постоянный ток и примыкающие к нулю частоты (фильтр нижних частот), то должно учитываться лишь одно слагаемое, соответствующее значению m = 0:

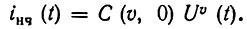
Для линейного детектора, т. е. при υ = 1, получаем

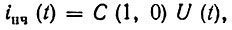
а для квадратичного детектора (однополупериодного), т. е. при υ = 2,

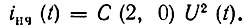
Как и следовало ожидать, в первом случае выходная величина пропорциональна первой степени, а во втором - квадрату огибающей входного напряжения.

При ограничителе с избирательной нагрузкой, выделяющей полосу частот вблизи ω₀, для слагаемого, соответствующего m = 1, получаем

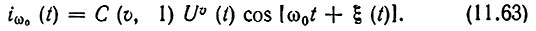
Из этого выражения вытекает важное заключение о структуре колебания на выходе резонансного ограничителя: частота и фаза колебания полностью совпадают соответственно с частотой и фазой входного воздействия. Закон изменения огибающей U^υ(t) зависит от формы вольт-амперной характеристики.

При υ = 0 (идеальный ограничитель) амплитуда выходного колебания постоянна, так что выражение (11.63) принимает вид

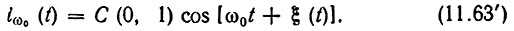
Коэффициенты С (υ, m), входящие в выражение (11.63), определяются на основе представления характеристики i(u) в виде контурного интеграла^*. Приведем значения трех коэффициентов, входящих в предыдущие выражения:

^** (См. [3], а также предыдущее издание настоящей книги.)

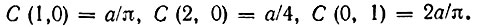
Эти коэффициенты можно получить также, рассмотрев гармоническое воздействие на нелинейный элемент (а узкополосный процесс в пределах одного периода близок к гармоническому).

Действительно, в режиме линейного однополупериодного детектирования, изображенном на рис. 11.11, т. е при угле отсечки тока 90°, среднее значение тока равно 1/π от амплитуды импульса. При квадратичной характеристике детектора оно равно 1/4. Амплитуда первой гармоники при полном ограничении, когда импульсы тока имеют форму прямоугольников, составляет 2/π от высоты импульса.

Спектральный состав тока i(t) в режиме υ = 0 (идеальное ограничение) представлен на рис. 11.12. На рис. 11.12, а показаны энергетический спектр W_x(ω) шума х(t) на входе ограничителя и спектральная плотность мощности гармонического колебания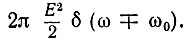

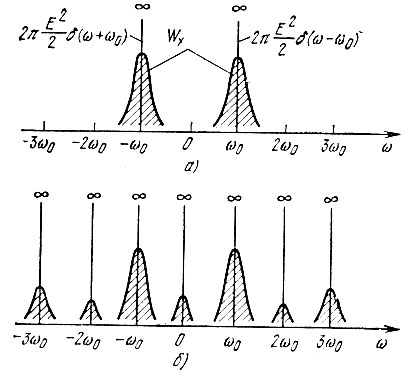
Рис. 11.12. Спектр на входе (а) и выходе (б) идеального ограничителя

На рис. 11.12, б показаны спектральные полосы шума и дискретные спектральные линии гармонических составляющих тока i(t) (с точностью до масштабных множителей). При узкополосном входном шуме и гармоническом сигнале, спектры которых сконцентрированы вблизи частоты ω₀, спектр тока i(t) группируется вблизи частот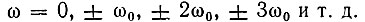

Вследствие резонансного характера нагрузки ограничителя надо учитывать энергетический спектр W_вых(ω) только в полосах, которые группируются вблизи частот 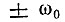(рис. 11.12). Следовательно, ток ограничителя, создающий напряжение на резонансной нагрузке, можно представить в виде суммы

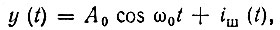
где i_ш(t) - узкополосное шумовое колебание с центральной частотой ω₀.

Подробный анализ [3] показывает, что мощность флуктуационной составляющей i_ш(t) (в главной спектральной полосе, вблизи 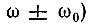составляет около 80% от всей мощности выходного шума.

Основной интерес представляет соотношение между мощностью полезного колебания, равной ¹/₂А²₀, и мощностью шума i_ш(t).

Характерной особенностью идеального ограничителя является независимость полной мощности (средней) суммарного колебания y(t) от соотношения мощностей на входе ограничителя. В любом случае эта мощность равна Р_у = ¹/₂ (2а/π)², где а - постоянная величина (см. рис. 11.11), определяющая амплитуду прямоугольных импульсов тока диода.

При отсутствии полезного сигнала (Е = 0) вся мощность Р_у сосредоточена в шуме. При отсутствии шумовой помехи на входе вся мощность Р_у сосредоточена в сигнале, причем величина амплитуды А₀ достигает при этом максимального значения А_{0 макс} = 2а/π.

При одновременном воздействии s(t) и х(t) амплитуда А₀ определяется выражением

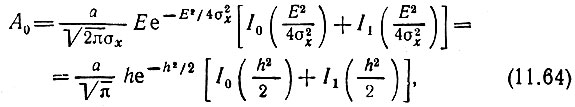
где I₀ и I₁ - функции Бесселя от мнимого аргумента (см. § 11.5), а h² = Е²/2σ²_x - отношение сигнал-помеха на входе ограничителя.

Для контроля заметим, что в отсутствие помехи, когда h → ∞ [см. [6] формула (8.451.5)],

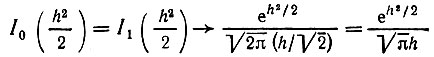
и выражение (11.64) дает A_{0 макс} = 2а/π.

В другом предельном случае 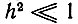(слабый сигнал), когда

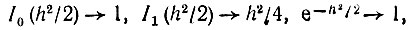
амплитуда сигнала

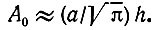
Отношение

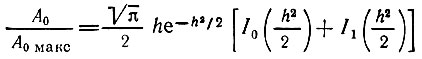
можно рассматривать как коэффициент ослабления сигнала помехой в ограничителе.

Приведем отношение сигнал - помеха (по мощности).

При слабом сигнале [3]

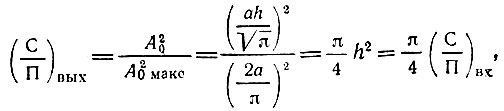
а при сильном сигнале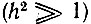

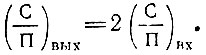
Итак, при 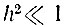относительное ослабление сигнала в ограничителе составляет всего лишь π/4. При сильном сигнале 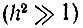отношение сигнал - помеха на выходе вдвое больше, чем на входе. Следует отметить, что относительное уменьшение дисперсии шума на выходе обусловлено подавлением составляющей, синфазной с сигналом. Дисперсия ортогональной составляющей шума, вызывающей флуктуацию фазы выходного сигнала, не уменьшается.