11.8. Корреляционная функция и энергетический спектр случайного процесса в параметрической цепи

Пусть передаточная функция линейной параметрической цепи является вещественной функцией времени и не зависит от частоты. В § 10.2 было показано, что подобная передаточная функция характеризует цепь, в которой имеет место амплитудная модуляция.

Обозначим передаточную функцию через К(t) (аргумент iω опущен), причем функция К(t) может представлять собой как детерминированный, так и случайный процесс. Входной сигнал s(t) также может быть либо детерминированным, либо случайным процессом.

Составим выражение для корреляционной функции выходного сигнала s_вых(t)

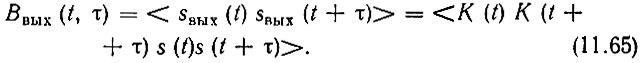
Нас интересует случай, когда передаточная функция К(t) не зависит от входного сигнала s(t). Тогда среднее значение произведения в (11.65) равно произведению средних значений соответствующих сомножителей, т. е.

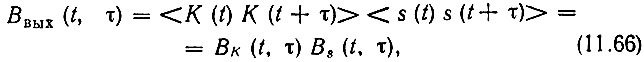
где В_s(t, τ) есть корреляционная функция входного сигнала, а

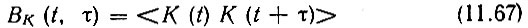
- корреляционная функция цепи с коэффициентом передачи К(t).

Из выражения (11.66) вытекает важное свойство линейной цепи с переменными параметрами: корреляционная функция выходного сигнала равна произведению корреляционных функций входного сигнала В_s(t, τ) и цепи В_K(t, τ).

Корреляционные функции в (11.66), (11.67) в случае нестационарных процессов зависят не только от временного сдвига τ, но и от времени t. Этими характеристиками не всегда удобно пользоваться. Далее в примерах используются функции В(τ), получаемые усреднением В(t, τ) по t [см. § 4.7, формулу (4.89)].

Применяя преобразование Фурье к усредненной по времени функции В_вых(τ), получаем также усредненный энергетический спектр выходного сигнала

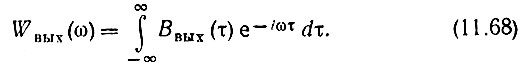
Проиллюстрируем соотношения (11.65)-(11.68) на примерах.

1. Гармонический сигнал s(t) = cos ω₀t действует на входе линейной цепи с передаточной функцией

где К₀ - среднее значение коэффициента усиления цепи; ΔК(t) - флуктуация коэффициента усиления, представляющая собой нормально распределенный стационарный случайный процесс с дисперсией σ²_К.

Для полной характеристики изменения во времени передаточной функции цепи должны быть заданы либо корреляционная функция B_K(τ), либо энергетический спектр W_K(ω) случайного процесса К(t).

Очевидно, что постоянной составляющей К₀ соответствует энергетический спектр W_K0(ω) = 2πК²₀δ(ω)^*. Энергетический спектр второго слагаемого, т. е. ΔК(t) зададим в форме

^* (Действительно, для постоянной составляющей К₀ корреляционная функция равна К²₀. Следовательно, по формуле (11.68) энергетический спектр

)

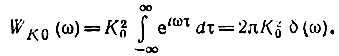
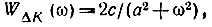
где a и c - постоянные величины.

Таким образом, энергетический спектр суммы К₀ + ΔК(t)

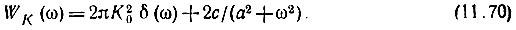
Заданному энергетическому спектру W_К(ω) соответствует корреляционная функция

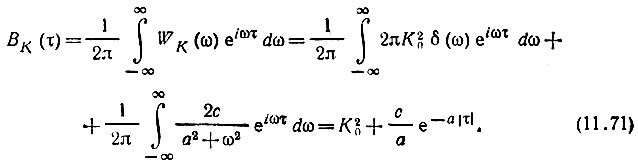
Найдем корреляционную функцию и энергетический спектр сигнала на выходе цепи.

Имея в виду соотношения (11.66) и (11.71), а также учитывая, что корреляционная функция сигнала s(t) = cos ω₀t равна

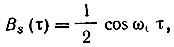
получаем

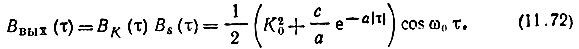
Находим теперь энергетический спектр с помощью выражения (11.68):

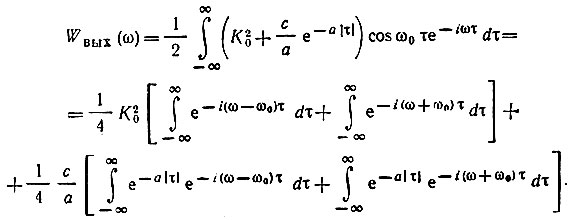
Первые два интеграла дают дельта-функции 2πδ(ω - ω₀) и 2πδ(ω + ω₀). Последние же два интеграла дают соответственно 2а/[а² + (ω - ω₀)2] и 2а/[а² + (ω + ω₀)²]. Таким образом, окончательно

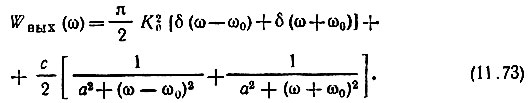
Функция W_вых(ω) изображена на рис. 11.13. Монохроматической составляющей выходного сигнала соответствуют две дискретные спектральные линии, а шумовой составляющей, обусловленной флуктуациями усиления ΔK(t), - сплошной спектр (на рис. 11.13 заштрихован). Этот спектр состоит из комбинационных частот, располагающихся симметрично относительно частоты сигнала ω₀ (в области отрицательных ω симметрично относительно - ω₀).

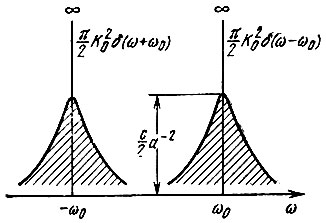
Рис. 11.13. Энергетический спектр на выходе параметрической цепи со случайной передаточной функцией при гармоническом воздействии

2. Нормально распределенный случайный процесс s(t) с энергетическим спектром (рис. 11.14)

группирующимся вблизи нулевой частоты, действует на входе цепи с передаточной функцией

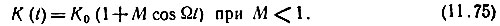
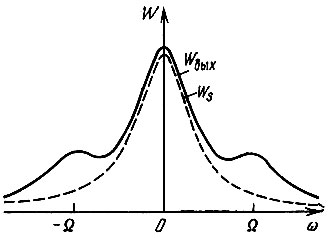
Рис. 11.14. Энергетический спектр на выходе параметрической цепи с передаточной функцией, изменяющейся по гармоническому закону, при воздействии нормальным случайным процессом

Находим корреляционную функцию входного сигнала

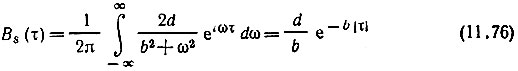
и корреляционную функцию цепи

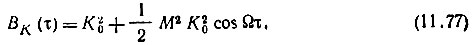
Тогда в соответствии с соотношением (11.66) корреляционная функция выходного сигнала

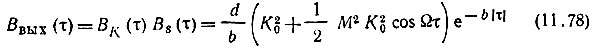
и энергетический спектр

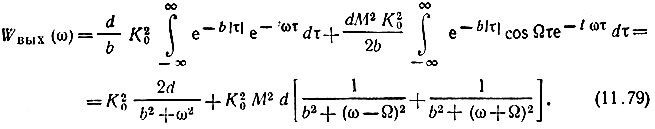
Функция W_вых(ω) изображена на рис. 11.14.

3. Нормально распределенный случайный процесс s(t) действует на входе цепи, передаточная функция К(t) которой является также случайным процессом с нормальным распределением.

Энергетические спектры процессов s(t) и K(t) зададим в форме W_s(ω) = 2d/(b² + ω²) - как в примере 2, W_K(ω) = 2πК²₀δ(ω) + 2с/(а² + ω²) - как в примере 1.

Корреляционные функции входного сигнала и рассматриваемой цепи соответственно равны

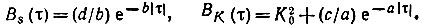
Находим корреляционную функцию выходного сигнала

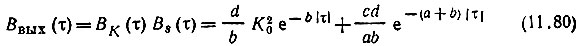
и энергетический спектр

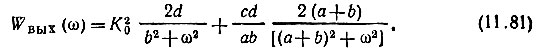
Первое слагаемое в правой части соответствует сигналу на выходе цепи с передаточной функцией K₀ (в отсутствие мультипликативной помехи), а второе слагаемое соответствует мультипликативной помехе. Величина этого слагаемого пропорциональна произведению параметра d, характеризующего интенсивность сигнала, и параметра с, который определяет дисперсию флуктуации передаточной функции цепи σ²_K.