11.9. Влияние мультипликативной помехи на закон распределения сигнала

Рассмотренные в предыдущем параграфе характеристики случайного сигнала - корреляционная и спектральная - не являются исчерпывающими. Для прикладных задач большой интерес представляет определение плотности вероятности р(s_вых).

В общем случае, когда передаточная функция цепи К(iω, t) является функцией двух переменных - частоты и времени, отыскать р(s_вых) при произвольном законе распределения входного сигнала весьма затруднительно. Задача сильно упрощается при мультипликативной помехе типа амплитудной модуляции, когда передаточная функция К(t) зависит только от одной переменной - времени t.

Имея в виду это условие, рассмотрим следующие три характерные ситуации:

1) s(t) - случайный, а К(t) - детерминированный процессы;

2) s(t) - детерминированный, а К(t) - случайный процессы;

3) s(t) и К(t) - случайные процессы.

Ситуации 1 и 2 приводят к задаче нахождения закона распределения произведения s(t), К(t),в котором один из сомножителей является случайной, а другой - детерминированной величиной. Если случайный процесс стационарный, задача легко решается. Из теории случайных функций известно, что при умножении случайной функции х(t) (стационарный процесс) с дифференциальным законом распределения р(х), с нулевым средним и дисперсией σ²_x на детерминированную функцию времени y(t) получается нестационарный процесс x(t) y(t) с прежним законом распределения, но с дисперсией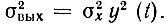

В частности, если входной сигнал s(t) - стационарный, нормально распределенный процесс с дисперсией σ²_s, а передаточная функция системы К(t) - детерминированная (случай 1), то выходной сигнал сохраняет нормальное распределение, однако каждому фиксированному моменту времени соответствует своя дисперсия σ²_вых = σ²_s К²(t).

При детерминированном сигнале s(t) и случайной функции К(t) (случай 2), если последнюю можно представить в форме К(t) = K₀ + ΔК(t), выходной сигнал целесообразно записать в виде

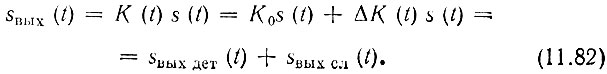
Первое слагаемое в правой части характеризует полезный выходной сигнал (детерминированный), а второе - мультипликативную помеху (случайную). Закон распределения этого слагаемого такой же, как у случайного процесса ΔК(t), но с дисперсией σ²_Ks²(t) (при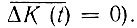

Рассмотрим случай 3. Пусть оба процесса s(t) и К(t) стационарные, с плотностями вероятности соответственно р(s) и р(K). Задача заключается в нахождении плотности вероятности случайного процесса s_вых(t), являющегося произведением s(t) и К(t).

Из теории вероятности известно, что если взаимно независимым случайным величинам x и y соответствуют плотности вероятности р(х) и р(y), то произведению z = xy соответствует плотность вероятности р(z), определяемая выражением

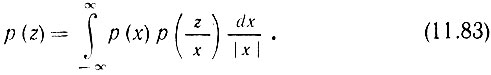
Подразумевая под х входной сигнал s(t), под у передаточную функцию К(t), а под z произведение s_вых(t) = s(t) К(t), получаем выражение для определения плотности вероятностей выходного сигнала s_вых. Применение (11.83) иллюстрируется примерами.

1. В качестве первого примера рассмотрим передачу гармонического сигнала s(t) = A₀ cos (ω₀t + θ), в котором начальная фаза θ является случайной величиной, равномерно распределенной на интервале (-π, π), через линейную цепь с передаточной функцией К(t), флуктуирующей относительно среднего значения K₀ по нормальному закону.

Таким образом, соответствующие плотности вероятности

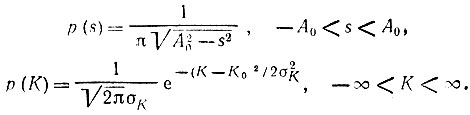
Подставляя эти выражения в (11.83) и приравнивая x = s, а z/x = y = s_вых/s = K, приходим к следующему общему выражению для плотности вероятности выходного сигнала:

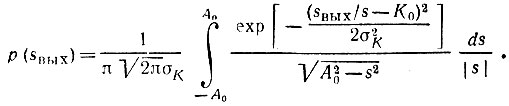
Следует подчеркнуть, что найденный закон распределения характеризует мгновенное значение выходного сигнала.

Для практики часто основной интерес представляет распределение огибающей выходного сигнала.

Представляя выходной сигнал в форме

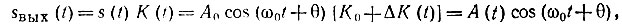
где А(t) = A₀ [К₀ + ΔK(t)] - огибающая, приходим к очевидному заключению, что случайность фазы θ не оказывает влияния на распределение огибающей. Последнее совпадает с распределением функции К(t), т. е. является нормальным, со средним значением A₀K₀ и с дисперсией A²₀σ²_K.

2. Обратимся теперь к анализу статистических характеристик случайного нормально распределенного сигнала s(t), пропущенного через цепь, передаточная функция которой К(t) также является нормально распределенной случайной величиной.

Для упрощения воспользуемся представлением передаточной функции в виде К(t) = К₀ + ΔК(t), в соответствии с чем выходной сигнал можно записать в виде суммы, аналогичной (11.82):

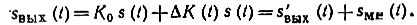
Первое слагаемое в правой части, отличающееся от s(t) постоянным коэффициентом K₀, характеризует полезный сигнал на выходе цепи. Статистические свойства этого сигнала совпадают со свойствами случайного сигнала s(t), действующего на входе цепи, а дисперсия равна K²₀σ²_s.

Рассмотрим слагаемое s_МП(t), являющееся результатом действия мультипликативной помехи. По условию

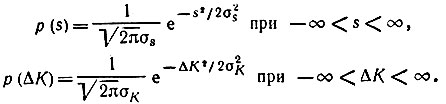
Подставляя эти выражения в (11.83), находим плотность вероятности помехи s_МП(t):

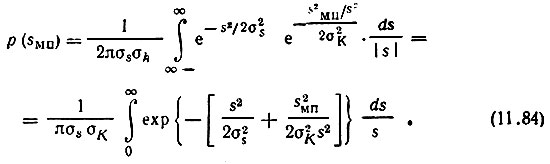
Входящий в это выражение интеграл является частным случаем интеграла (см. [6], формула (3.478.4))

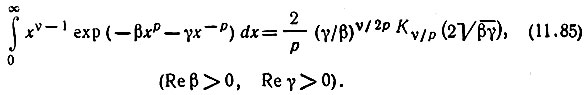
Здесь K_μ/p(z) - цилиндрические функции мнимого аргумента.

Приравнивая в соответствии с (11.84) 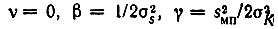и р = 2, получаем

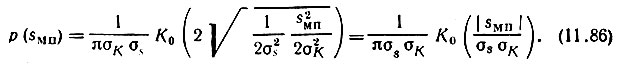
Обозначение цилиндрической функции нулевого порядка К₀ не следует смешивать со средним значением передаточной функции К(t) [см. (11.69)].

Для вычисления функции К₀(z) можно использовать ряд (см. [6], формула (8.447.3))

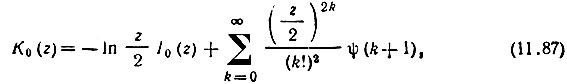
I₀(z) - функция Бесселя от мнимого аргумента; ψ - функция Эйлера

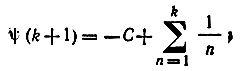
С = 0,5772 - постоянная Эйлера.

С учетом (11.87) выражение (11.86) переходит в следующее:

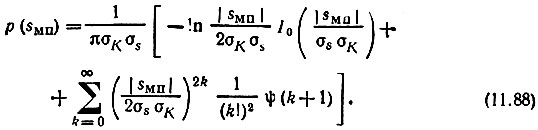
График функции σ_sσ_Кp (s_МП) изображен на рис. 11.15. Этот график имеет обобщенный характер, иллюстрирующий закон распределения произведения двух нормальных взаимно независимых случайных процессов в дисперсиями σ²_s и σ²_К и с нулевыми средними.

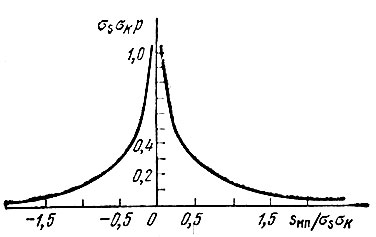
Рис. 11.15. Плотность вероятности произведения двух независимых нормальных случайных процессов

3. Допустим, что входной сигнал представляет собой узкополосный нормально распределенный процесс

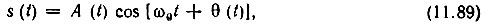
причем огибающая A(t) и функция ΔК(t) обладают примерно одинаковыми по ширине энергетическими спектрами.

Тогда колебание s_МП(t) удобно представить в форме, аналогичной (11.89):

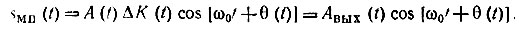
Для практики часто требуется знать закон распределения огибающей А_вых(t), т. е. случайной функции

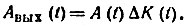
Учитывая, что А обладает релеевским распределением:

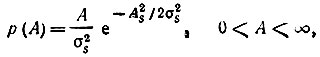
а ΔК(t) - нормальным распределением:

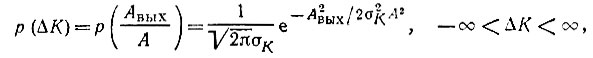
в соответствии с (11.83) получаем

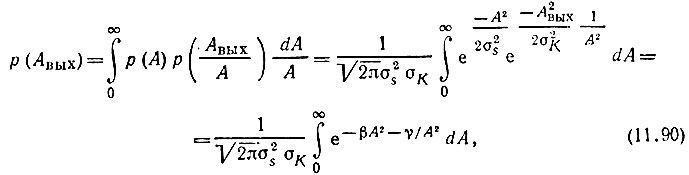
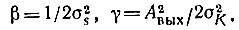
Интеграл в выражении (11.90) является частным случаем интеграла (11.85) при γ = 1 и р = 2.

Таким образом,

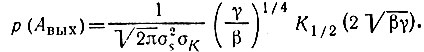
Учитывая, что (см. [6], формула (8.469.3))

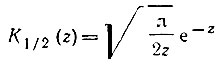
и подставляя значения β и γ, получаем

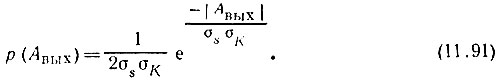
График функции 2σ_sσ_Kp (А_вых) изображен на рис. 11.16. В отличие от огибающей А(t), которая не может принимать отрицательных значений, величина А_вых(t), являющаяся произведением А(t) и ΔK(t), имеет симметричное относительно нуля распределение (экспоненциальное).

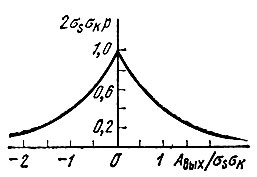
Рис. 11.16. Плотность вероятности огибающей случайного процесса на выходе параметрической цепи со случайной передаточной функцией при воздействии нормальным процессом