Приложение II. Корреляционная функция сигнала на плоскости время - частота

В предыдущих главах корреляционная функция использовалась для оценки степени связи сигнала s(t) со своей копией s(t + τ), сдвинутой на величину τ во времени.

Аналогичная задача возникает при определении сдвига спектра узкополосного сигнала на оси частот. Поэтому целесообразно обобщить понятие корреляционной функции при одновременном сдвиге сигнала по времени и по частоте.

Исходное колебание запишем в форме

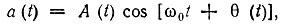
а то же колебание, сдвинутое на время τ и смещенное по частоте на Ω = 2πF, как

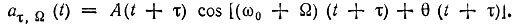
Переходя к аналитическим сигналам, получаем соответственно:

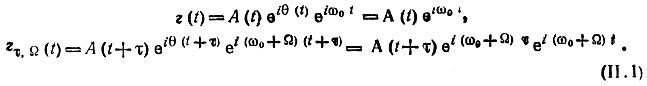
Тогда корреляционная функция аналитического сигнала может быть определена выражением [см. (3.94) и (3.97)]

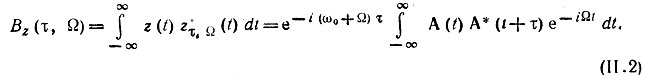
Полученное выражение, учитывающее как сдвиг сигнала а(t) во времени так и смещение по частоте (Ω = 2πF), называется обобщен ной корреляционной функцией.

Модуль выражения (II.2)

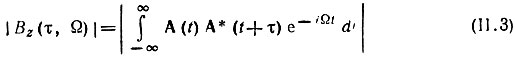
получил название двумерной корреляционной функции.

Большое распространение в теории сигналов получила нормированная двумерная корреляционная функция

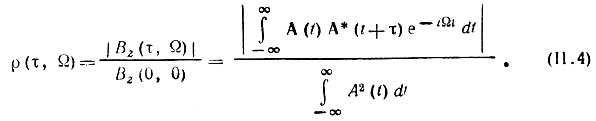
В прямоугольной системе координат τ, Ω, ρ функция ρ(τ, Ω) изображается в виде поверхности, пример которой для радиоимпульса гауссовой формы (о немодулированным высокочастотным заполнением) приведен на рис. II.1.

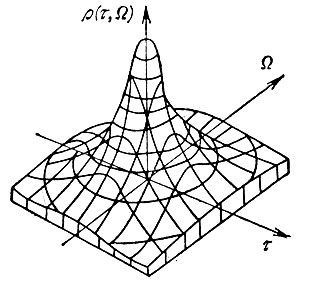
Рис. II.1. Тело неопределенности радиоимпульса гауссовой формы

Непосредственно из выражения (II.4) вытекает что максимальное значение функции ρ(τ, Ω), т. е. ρ(0, 0), равно единицы.

Оказывается, что и объем тела, ограниченного плоскостью ρ = 0 и поверхностью ρ²(τ, Ω), равен единице, независимо от законов модуляции амплитуды и фазы сигнала [1, 13]:

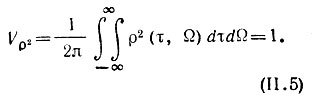
Если изменением закона модуляции сжать тело под поверхностью ρ²(τ, Ω) по оси τ, оно расплывается по оси Ω; сжатие по оси Ω приводит к растяжению по оси τ.

Это указывает на невозможность одновременного повышения разрешающей способности сигнала по времени и по частоте, а соотношение (11.5) является математической формулировкой принципа неопределенности в радиолокации.

В связи с этим двумерную корреляционную функцию сигнала ρ(τ, Ω) часто называют функцией неопределенности, а тело, ограниченное плоскостью ρ = 0 и поверхностью ρ²(τ, Ω), - телом неопределенности (рис. II.1).

Положив в (II.2) Ω = 0, получим выражение

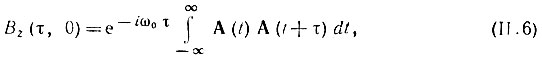
совпадающее с (3.97).

Для перехода к корреляционной функции В_а(τ) физического колебания a(t) = А(t) cos [ω₀t + θ(t)] нужно в соответствии с (3.96) выделить вещественную часть В_z(τ, 0). Интеграл в выражении (11.6) определяет комплексную огибающую функции В_z(τ, 0), а быстро осциллирующий множитель е^iω₀τ - высокочастотное заполнение этой функции.

Переходя к модулю и учитывая, что 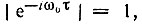получаем

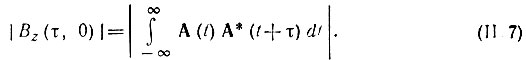
Из этого выражения следует, что сечение поверхности тела неопределенности плоскостью Ω = 0 определяет огибающую корреляционной функции В_a(τ) колебания

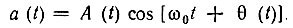
С другой стороны, положив в (II.3) τ = 0, получим выражение

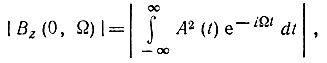
которое на основе выражений (2.61) и (2.62) можно преобразовать к форме

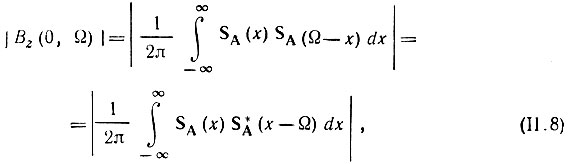
где S_A(ω) - спектральная плотность огибающей A(t).

Таким образом, сечение поверхности тела неопределенности плоскостью τ = 0 определяет функцию частотной корреляции, т. е. степень связи спектра S_A(ω) со своей копией, сдвинутой по оси частот на величину Ω.

Определяемая выражением (II.4) двумерная корреляционная функция ρ(t, Ω) приобретает особое значение при согласованной фильтрации сигнала. В гл. 12 было показано, что сигнал на выходе согласованного фильтра совпадает с корреляционной функцией входного сигнала. Следовательно, корреляционную функцию |B_z(τ, 0)| можно использовать для оценки разрешающей способности сигнала по времени, а функцию |B_z(0, Ω)| - по частоте.

Эти свойства функции неопределенности лежат в основе теории разрешающей способности радиолокационных устройств при определении дальности цели и скорости ее движения.