Приложение I. Сигнал с минимальным произведением длительности на полосу частот

В § 2.10 отмечалось, что произведение длительности сигнала на его полосу частот не может быть меньше некоторой определенной величины. Найдем эту величину, а также оптимальный сигнал, обладающий минимально возможным произведением длительность × полоса частот.

Необходимо сначала условиться об определении понятий длительность сигнала и ширина спектра сигнала. В практике применяются различные определения, выбор которых зависит от назначения сигнала, а также от формы сигнала и его спектра. В некоторых случаях выбор является произвольным. Так, длительность сигнала прямоугольной формы естественно определять как основание прямоугольника, однако ширина спектра определяется либо как основание главного лепестка (например, в § 2.9.1), либо на уровне 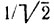от максимального значения. Длительность гауссова импульса (§ 2.9.2) и ширина его спектра определяются на уровне 0,606 от максимального значения. Иногда пользуются энергетическим критерием, понимая под шириной спектра полосу частот, содержащую заданную долю от полной энергии сигнала.

Для выявления предельных соотношений, связывающих длительность и частотную полосу, в современной теории сигналов большое распространение получил метод моментов.

По аналогии с понятием момента инерции в механике эффективную длительность сигнала s(t) можно определить выражением

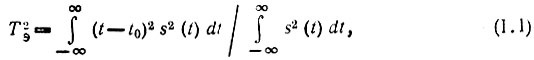
где середина импульса t₀ определяется из условия

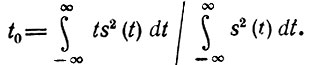
Имеется в виду, что функция s(t) интегрируема с квадратом (сигнал с конечной энергией).

Аналогично эквивалентная ширина спектра 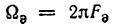определяется выражением^*

^* (Имеются в виду сигналы без высокочастотного заполнения.)

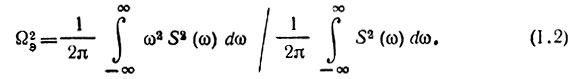
Так как модуль спектра S(ω) не зависит от смещения s(t) во времени, можно положить t₀ = 0. Наконец, сигнал s(t) можно нормировать таким образом, чтобы его энергия Э равнялась единице, и, следовательно,

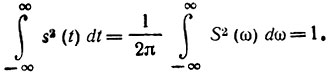
При этих условиях выражения для T_э и Ω_э принимают вид

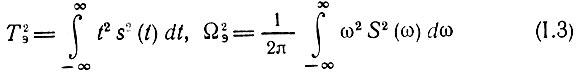
и, следовательно, произведение длительности сигнала на ширину спектра равно

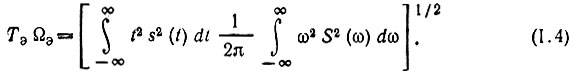
Нужно иметь в виду, что T_э и Ω_э являются среднеквадратическими отклонениями соответственно от t = t₀ и ω = 0. Полную длительность сигнала следует приравнять 2 T_э, а полную ширину спектра (включая и область отрицательных частот) - 2 Ω_э.

Метод моментов применим не к любым сигналам. Из выражений (1.3) видно, что функция времени s(t) с увеличением t должна убывать быстрее, чем 1/t, а функция S(ω) - быстрее, чем 1/ω, так как в противном случае соответствующие интегралы стремятся к бесконечности (расходятся).

В частности, это относится к спектру строго прямоугольного импульса:

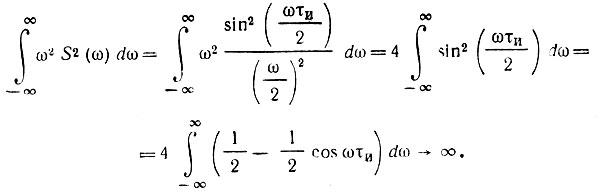
Однако для физически реализуемых сигналов требование достаточно быстрого убывания s(t) и S(ω) выполняется.

Найдем нижний предел произведения T_эΩ_э.

Известно, что iωS(ω) есть спектральная плотность производной от сигнала s(t). Следовательно, второй интеграл в правой части (1.4) на основании равенства Парсеваля можно приравнять

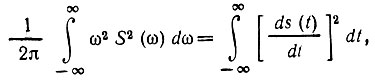
после чего (1.4) переходит в следующее выражение:

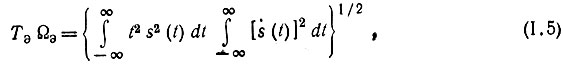
где обозначено

Воспользуемся теперь неравенством Шварца [см. (12.11)], которое применительно к выражению (1.5) принимает вид

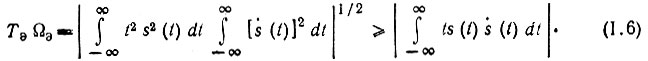
Правая часть этого неравенства после интегрирования по частям приводится к выражению

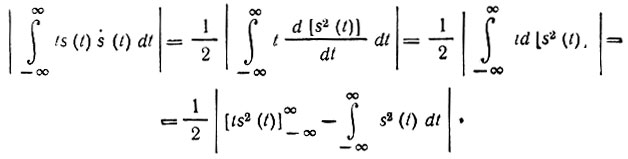
Оговоренное выше условие интегрируемости сигнала s(t) с квадратом позволяет опустить первое слагаемое в правой части. Учитывая нормирование сигнала (Э = 1), получаем для произведения T_эΩ_э неравенства T_эΩ_э > 1/2 или T_эF_э > 1/4π.

Итак, величина произведения T_эF_э, зависящая от формы сигнала, в любом случае не может быть меньше 1/4π.

Найдем теперь сигнал, обладающий минимально возможной величиной T_эF_э. Эта задача сводится к отысканию функции s(t), обращающей неравенство (1.6) в равенство.

Непосредственно из (1.6) очевидно условие равенства:

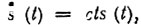
где с - постоянный коэффициент.

Таким образом, получаем уравнение

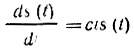
или

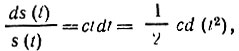
которое легко интегрируется

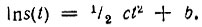
Отсюда искомая функция

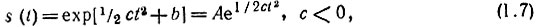
- гауссов импульс.

[Отрицательность с вытекает из условия интегрируемости функции s(t).]

В частности, для гауссова импульса, рассмотренного в примере 2, § 2.9 эффективная длительность, вычисленная по формуле (1.3), равна 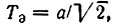а эффективная ширина спектра 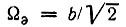(произведение Т_эΩ_э = аb/2 = ¹/₂, T_эF_э = 1/4π = 0,0795).

Соответственно полная длительность импульса 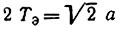и ширина спектра 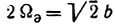Заметим, что аналогичные параметры гауссова импульса, определяемые на уровне е^-1/2 = 0,606, составляют 2а и 2b (вместо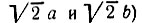

Для треугольного импульса, спектральная плотность которого (рис. I.1, а и б)

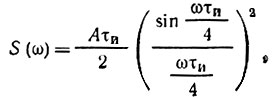
параметры T_э и F_э равны:

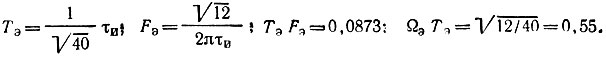
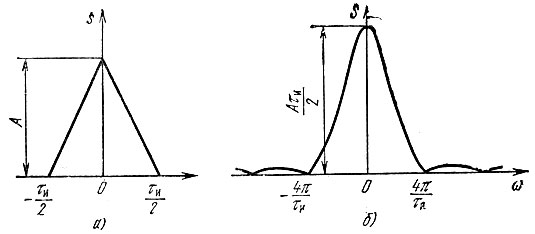
Рис. I.1. Импульс треугольной формы (а) и его спектральная плотность (б)

Как видим, величина произведения длительность × полоса частот у треугольного импульса всего лишь на 10% больше, чем у гауссова импульса.

Из приведенных выше соотношений следует, что сжатие импульса во времени с целью, например, повышения точности измерения момента его появления неизбежно сопровождается расширением спектра импульса, что заставляет расширять полосу пропускания измерительного устройства. Аналогично сжатие спектра импульса с целью повышения точности измерения частоты неизбежно сопровождается растяжением сигнала во времени, что требует удлинения времени наблюдения (измерения). Невозможность одновременно сконцентрировать сигнал в узкой полосе частот и в коротком интервале времени представляет собой одно из проявлений известного в физике принципа неопределенности.