15.13. Некоторые особенности синтеза цифровых фильтров

Как и аналоговые, цифровые фильтры обычно синтезируются на основе передаточной функции, представленной в виде рациональной дроби (13.64). В результате соответствующей аппроксимации заданной передаточной функции Кˆ(z) определяется положение нулей и полюсов на z-плоскости, после чего находятся весовые коэффициенты а_n и b_m, входящие в полиномы в выражении (13.63).

Цифровой фильтр можно реализовать либо в виде совокупности простых звеньев (первого или второго порядка), либо в виде канонической схемы, описанной в § 13.6 (рис. 13.14).

При разбиении фильтра на простые звенья отпадают все ограничения, отмеченные в § 15.4 по отношению к аналоговым цепям. В цифровых цепях вопросы согласования входных, выходных и нагрузочных сопротивлений, а также вопросы развязки отдельных звеньев вообще не возникают. В связи с этим наряду с каскадным (последовательным) соединением простых звеньев широко применяется параллельное их включение.

В первом случае функция (13.64) записывается в виде произведения простых множителей, каждый из которых является передаточной функцией звена (см. аналогичное разбиение в § 15.4). Во втором случае функция (13.64) разлагается на простые дроби

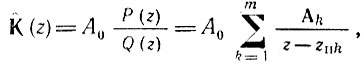
где 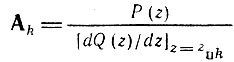- вычет функции 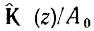в полюсе z_пk.

Если знаменатель Q(z) содержит всего m корней, из которых m₁ - число вещественных (лежащих на действительной оси), а m₂ - число комплексно-сопряженных пар корней (m = m₁ + 2m₂), то

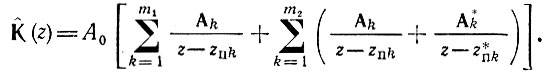
Это выражение легко приводится к виду

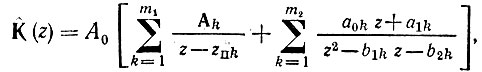
где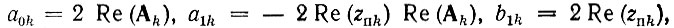

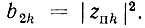
Как в каскадной, так и в параллельной схеме отдельные звенья реализуются по схеме, описанной в § 13.10 (рис. 13.24). Весовые коэффициенты звена второго порядка определяются по формуле (13.76), а первого порядка - непосредственно из передаточной функции звена.

При аппроксимации заданной характеристики цифрового фильтра широко распространен метод, основанный на использовании результатов аппроксимации соответствующего аналогового фильтра. Суть этого метода заключается в следующем. Пусть задан физически осуществимый аналоговый фильтр с передаточной функцией К(р), удовлетворяющей предъявляемым к фильтру требованиям, и нужно осуществить эквивалентный ему (в определенном смысле) цифровой фильтр. Полюса и нули функции К(р) предполагаются известными.

Поскольку искомая передаточная функция цифрового фильтра 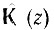однозначно определяется своими полюсами и нулями на z-плоскости, а между z и р существует соотношение z = е^рТ (см. § 13.7), на первый взгляд представляется логичным воспользоваться выражениями 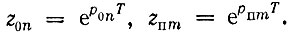В действительности же такой подход может при некоторых условиях оказаться ошибочным. В § 13.10 на примере RC-цепи было показано, что использование преобразования z = е^Рт приводит к дискретной импульсной характеристике g_T(t), совпадающей с отсчетами непрерывной характеристики g(t) аналоговой цепи, но при этом совершенно искажается амплитудно-частотная характеристика. Аналогичный результат получается и для более сложных цепей. В связи с этим метод синтеза, основанный на преобразовании z = е^рT, получил название метода инвариантного по отношению к импульсной характеристике фильтра.

Для осуществления синтеза, инвариантного по отношению к амплитудно-частотной характеристике, следует применить преобразование, при котором бы вся мнимая ось iω р-плоскости отображалась на z-плоскости одним обходом окружности радиуса |z| = 1.

Этому требованию отвечает билинейное (дробно-рациональное) преобразование

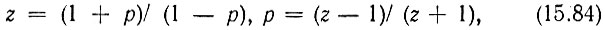
где 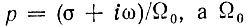- произвольная постоянная, обеспечивающая безразмерность величины р, выбираемая исходя из соображений нормирования.

Действительно, приравнивая 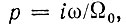получаем выражение

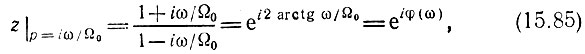
из которого следует, что перемещению точки р вдоль оси iω/Ω₀ соответствует перемещение точки z по окружности радиуса |z| = 1, как и при обычном z-преобразовании (z = е^iωT). Отличие билинейного преобразования заключается в том, что при увеличении ω аргумент φ(ω) возрастает нелинейно: при стремлении ω к ±∞ φ(ω) стремится к своим предельным значениям ±π. Таким образом, вся ось iω p-плоскости трансформируется на z-плоскости в один обход окружности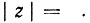

Введя обозначение φ(ω) = ω_цT, можем записать

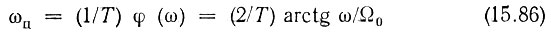
и соответственно

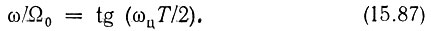
Если задана амплитудно-частотная характеристика аналоговой цепи, то при использовании билинейного z-преобразования АЧХ эквивалентного цифрового фильтра, сохраняя масштаб по оси ординат, сжимается по оси абсцисс в пределах -π ≤ ω_цT < π.

Поясним это на примере синтеза цифрового фильтра нижних частот. Пусть задана частота среза ω_сц и период дискретизации T. Требования к равномерности АЧХ в полосе пропускания зададим такие же, что и для аналогового фильтра Чебышева (при n = 2), рассчитанного в § 15.9. Передаточная функция этого фильтра определяется полюсами 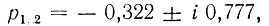а амплитудно-частотная характеристика, построенная по формуле

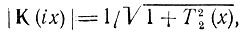
представлена на рис. 15.24, а.

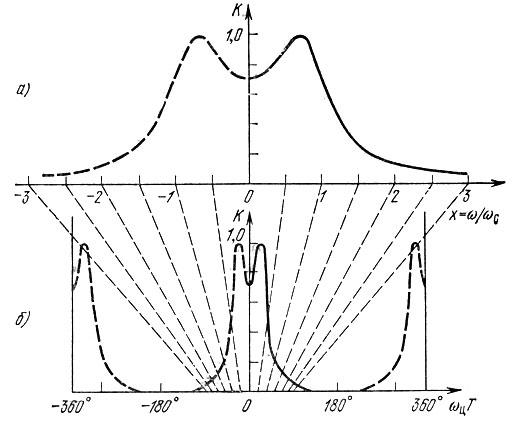
Рис. 15.24. Амплитудно-частотные характеристики аналогового (а) и соответствующего ему цифрового фильтра (б)

Для построения АЧХ цифрового фильтра и нахождения полюсов передаточной функции Кˆ(z), что требуется для определения весовых коэффициентов фильтра, необходимо предварительно найти нормирующую частоту Ω₀. Это можно сделать, установив соответствие между частотами среза ω₀ и ω_сц аналогового и цифрового фильтров. Для этого подставим в правую часть выражения (15.87) ω_c = ω_сц, а в левую часть ω = ω_c:

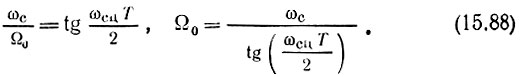
Теперь выражение (15.86) можно записать в форме

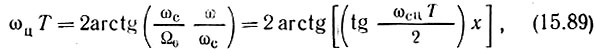
где x = ω/ω_c - нормированная частота, использованная при аппроксимации АЧХ аналогового фильтра.

Пусть, например, частота среза цифрового фильтра должна составлять 10% от частоты дискретизации 1/Т. Тогда ω_сцT = 0,1⋅2 π и

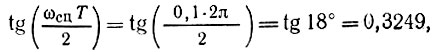
а выражение (15.89) переходит в

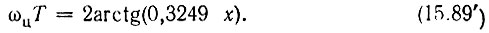
Это соотношение между ω_цТ и х позволяет построить АЧХ синтезируемого цифрового фильтра по заданной характеристике исходного аналогового фильтра (рис. 15.24, б). Видно, что деформация АЧХ из-за сжатия по оси абсцисс проявляется лишь при значительном удалении ω_цТ от нуля. В полосе пропускания обе характеристики практически совпадают.

Определим параметры схемы цифрового фильтра. Сначала найдем полюса z_п1 и z_п2 по заданным полюсам р₁ и р₂.

Переменную р в выражении (15.84) следует представить в форме

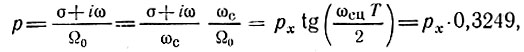
где р_х = (σ + iω)/ω_c совпадает с переменной р в выражении (15.71).

Таким образом, для рассматриваемого фильтра выражение (15.84) можно записать в виде

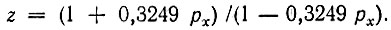
Подставив р_х = р₁ = -0,322 + i⋅0,777, получим

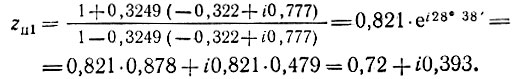
Соответственно

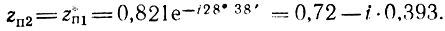
Искомую передаточную функцию 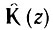можно получить подстановкой р = (z - 1)/(z + 1) в функцию 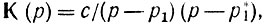где

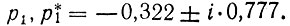
Таким образом,

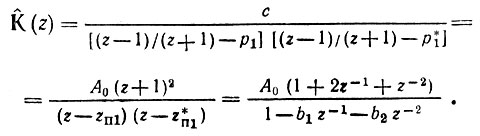
Итак, применение билинейного z-преобразования привело к появлению в передаточной функции двухкратного нуля (в точке z = -1).

Схема фильтра совпадает со схемой, представленной на рис. 13.24. В данном случае коэффициенты в обратных связях (см. § 13.11, п. 3)

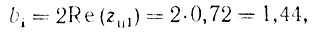
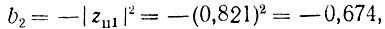
а в прямых связях: a0=l, ax - 2 и a2= 1.

Постоянный коэффициент А₀ введен для нормирования. При ω_ц = 0 z = 1 и функция 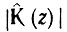по условию должна равняться единице, как и функция К(р) при ω = 0. При указанных выше коэффициентах a_i и b_i получается А₀ = 0,0585.

При синтезе цифрового фильтра существенное значение имеет выбор числа разрядов в преобразователе А/Ц, а также в арифметическом устройстве, исходя из допустимого уровня шумов квантования и округления (см. § 13.12 и 13.14).

Иначе обстоит дело с весовыми коэффициентами b₁ и b₂. Для точного представления этих коэффициентов в двоичной системе счисления может потребоваться значительное число разрядов (1,011101 для b₁ и 0,10101101 для b₂). Однако ценой несущественного отклонения амплитудно-частотной характеристики от заданной обычно можно значительно сократить число разрядов. Так, например, при загрублении весовых коэффициентов до b₁ = 1,0111 (1,4375) и b₂ = 0,1011 (0,687) получается АЧХ, практически совпадающая с заданной.