1.3. Физические основы и методы определения местоположения целей

Проблема определения местоположения какой-либо цели сводится к определению геометрических величин, однозначно характеризующих место цели в пространстве.

Радиоволны в однородной среде распространяются, как известно, прямолинейно и с постоянной скоростью. Эти свойства радиоволн позволяют определить направление на излучатель радиоволн и длину траектории распространения радиоволн.

Реальная среда в общем случае не является однородной. Поэтому траектория распространения радиоволн не будет строго прямолинейной, а скорость распространения радиоволн не будет строго постоянной на всем пути распространения.

Отмеченное обстоятельство хотя и ведет к понижению точности определения направления на излучатель и длины траектории распространения, однако не исключает возможности их определения.

Определение направления на излучатель радиоволн называется радиопеленгацией, а радиотехнические устройства, предназначенные для этих целей, называются радиопеленгаторами.

Определение длины траектории распространения радиоволн называется радиодальнометрией, а радиотехнические устройства, предназначенные для этих целей, называются радиодальномерами.

Таким образом, при помощи радиотехнических средств можно определить следующие геометрические величины:

1) пеленг α_М искомой точки М из фиксированной точки А (рис. 1.5),

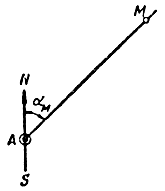
Рис. 1.5. Определение пеленга искомой точки из фиксированной

2) пеленг α_А фиксированной точки А из искомой точки М (рис. 1.6),

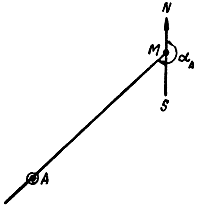
Рис. 1.6. Определение пеленга фиксированной точки из искомой

3) разность пеленгов α_р двух фиксированных точек А и В из искомой точки М (рис. 1.7),

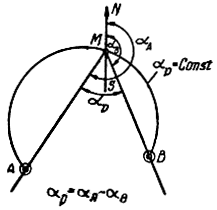
Рис. 1.7. Определение разности пеленгов двух фиксированных точек из искомой

4) расстояние от искомой точки М до фиксированной точки А (рис. 1.8),

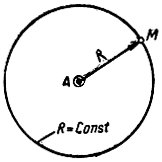
Рис. 1.8. Определение расстояния от искомой точки до фиксированной

5) разность расстояний от искомой точки М до двух фиксированных точек А и В (рис. 1.9) и

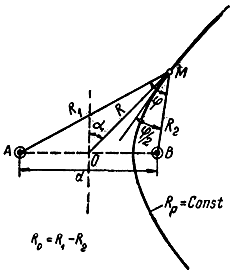
Рис. 1.9. Определение разности расстояний от искомой точки до двух фиксированных

6) сумму расстояний от искомой точки М до двух фиксированных точек А и В (рис. 1.10).

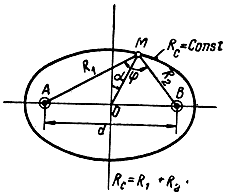
Рис. 1.10. Определение суммы расстояний от искомой точки до двух фиксированных

Здесь пеленгом называется угол между условно выбранным начальным направлением и искомым направлением. В качестве начального направления при пеленгации в горизонтальной плоскости обычно принимают северное направление географического меридиана. В этом случае пеленг называется истинным. Пеленг, отсчитываемый относительно бортовой оси корабля или самолета, называется бортовым. За положительное направление отсчета пеленга принимают направление вращения часовой стрелки.

Рассмотрим теперь методы определения местоположения цели на плоскости.

Если будет измерена одна из выше перечисленных геометрических величин, то будет найдена линия возможных местоположений цели.

Геометрическое место точек, для которых геометрическая величина, определяющая местоположение цели, постоянна, называется линией положения или позиционной линией.

При неизменном пеленге искомой точки из фиксированной (1.5) так же, как и при неизменном пеленге фиксированной точки из искомой (рис. 1.6) линии положения представляют собой прямую линию.

При неизменной разности пеленгов двух фиксированных точек из искомой линия положения представляет собой часть окружности, проходящей через точки А, В и М (рис. 1.7).

При неизменном расстоянии от искомой точки до фиксированной линия положения представляет собой окружность с центром в точке А и проходящую через точку М (рис. 1.8).

При неизменной разности расстояний от искомой точки до двух фиксированных линия положения представляет собой гиперболу, проходящую через подвижную точку М (рис. 1.9). Фиксированные точки А и В будут фокусами этой гиперболы.

При неизменной сумме расстояний от искомой точки до двух фиксированных линия положения представляет собой эллипс, проходящий через подвижную точку М (рис. 1.10). Фиксированные точки А и В будут фокусами этого эллипса.

Различным постоянным значениям каждой из перечисленных геометрических величин соответствует семейство линий положения.

В первом и втором случаях линии положения представляют собой семейство радиальных прямых; в третьем - семейство окружностей, проходящих через две фиксированные точки; в четвертом - семейство концентрических окружностей; в пятом - семейство софокускых гипербол и, наконец, в шестом - семейство софокусных эллипсов.

Для определения местоположения цели необходимо найти две пересекающиеся линии положения. Тогда точка пересечения линий положения и даст искомое местоположение. При этом могут быть использованы линии положения различных видов.

Из всех возможных методов местоопределения широкое распространение получили следующие:

1) пеленгационный, при котором местоположение цели определяется как точка пересечения двух прямых (рис. 1.11).

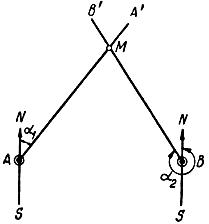
Рис. 1.11. Пеленгационный метод определения места

2) дальномерный, при котором местоположение цели определяется как точка пересечения двух окружностей (рис. 1.12),

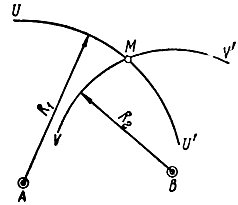
Рис. 1.12. Дальномерный метод определения места

3) разностно-дальномерный, при котором местоположение цели определяется как точка пересечения двух гипербол (рис. 1.13),

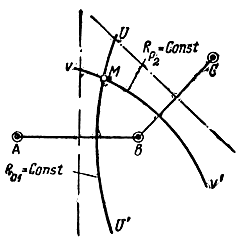
Рис. 1.13. Разностно-дальномерный метод определения места

4) дальномерно-пеленгационный, при котором (местоположение цели определяется как точка пересечения прямой с окружностью (рис. 1.14).

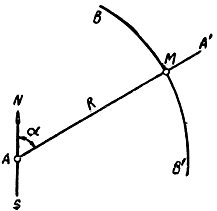
Рис. 1.14. Дальномерно-пеленгационный метод определения места

Пеленгационный метод получил широкое распространение в радионавигации в силу относительной простоты устройства радиопеленгаторов. В радиолокации этот метод используется сравнительно редко и только в тех случаях, когда по каким-либо причинам нельзя производить дальнометрию. Такой случай может иметь место, например, при наличии на объекте, местоположение которого определяется, генератора помех, нарушающего работу дальномера.

Дальномерный метод используется главным образом в радионавигации и реже в радиолокации.

Разностно-дальномерный метод используется только в радионавигации.

Дальномерно-пеленгационный метод является основным в радиолокации в силу того, что это единственный метод, позволяющий однозначно определить местоположение цели из одной точки. Все остальные способы требуют нескольких фиксированных точек (две, три или четыре), которые во избежание больших ошибок местоопределения должны быть разнесены на расстояния, соизмеримые с расстоянием от каждой из этих точек до искомой.

Рассмотрим теперь методы местоопределения в пространстве. В этом случае постоянному значению любой из перечисленных выше геометрических величин соответствует поверхность возможных местоположений объекта, которая называется поверхностью положения или позиционной поверхностью.

Так, например, постоянному значению расстояния от фиксированной точки до искомой соответствует поверхность положения в виде сферы, а постоянному значению пеленга в горизонтальной плоскости искомой точки из фиксированной соответствует вертикальная плоскость, проходящая через эти точки.

Местоположение цели в пространстве определяется как точка пересечения линии положения с поверхностью положения.

Наибольшее распространение получил дальномерно-пеленгационный метод, когда искомое местоположение определяется как точка пересечения прямой со сферой. В этом случае для однозначного определения направления на цель необходимо осуществить пеленгацию в двух пересекающихся плоскостях. Обычно пеленгацию осуществляют в горизонтальной и вертикальной плоскостях (рис. 1.15).

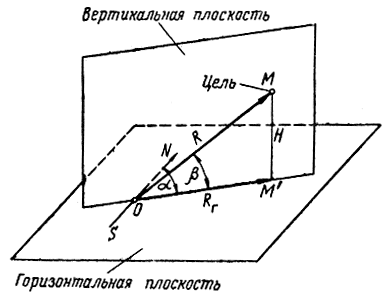
Рис. 1.15. Определение местоположения цели в пространстве

Угол α между северным направлением географического меридиана и проекцией направления на цель на горизонтальную плоскость называется азимутом цели. За положительное направление отсчета азимута принято направление вращения часовой стрелки.

Угол β между направлением на цель и горизонтальной плоскостью называется углом места цели. За положительное направление отсчета угла места принято направление снизу вверх.

Расстояние R от радиолокатора до цели называется наклонной дальностью.

Таким образом, задача местоопределения цели в пространстве дальномерно-пеленгационным методом сводится к измерению трех геометрических величин: наклонной дальности, азимута и угла места.