1.4. Основные тактико-технические параметры радиолокаторов

Основными тактическими параметрами радиолокаторов являются: область обзора, время обзора, определяемые координаты, точность определения координат, разрешающая способность, помехозащищенность.

Под областью обзора понимают ту область пространства, в пределах которой цель может быть обнаружена с вероятностями правильного обнаружения и ложной тревоги не хуже заданных. Область обзора характеризуется пределами обнаружения по дальности, т. е. максимальной и минимальной дальностью обнаружения, сектором обзора по азимуту и сектором обзора по углу места.

Под временем обзора понимают время, в течение которого происходит однократный просмотр области обзора, т. е. время полного цикла перемещения луча антенны радиолокатора в пределах телесного угла обзора.

Дело в том, что как с точки зрения увеличения максимальной дальности радиообнаружения, так и с точки зрения повышения точности пеленгации целесообразно уменьшать ширину диаграммы направленности антенны радиолокатора. Однако применение антенн с узкими диаграммами направленности влечет за собой необходимость периодического перемещения луча антенны в пространстве с целью обеспечения последовательного просмотра всей заданной области обзора. Такой просмотр пространства требует, конечно, определенного времени, которое определяется величиной области обзора, видом обзора и его режимом.

Из всех возможных видов обзора наибольшее распространение получили круговой (рис. 1.16), секторный, винтовой (рис. 1.17) и строчный (рис. 1.18).

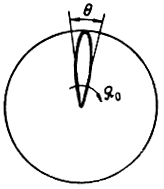
Рис. 1.16. Круговой обзор пространства

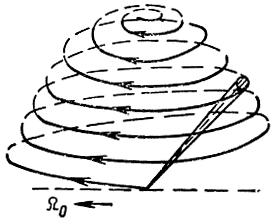
Рис. 1.17. Винтовой обзор пространства

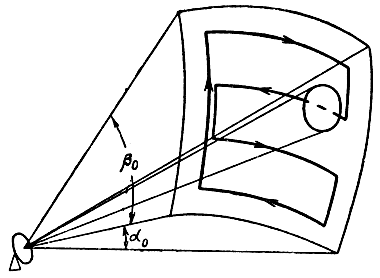
Рис. 1.18. Строчный обзор пространства

Круговой обзор осуществляется путем вращения антенны радиолокатора относительно вертикальной оси. Такой вид обзора широко используется в наземных радиолокаторах дальнего обнаружения и в самолетных радиолокаторах обзора земной поверхности.

При круговом обзоре время обзора

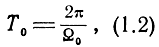
где Ω₀ - угловая скорость обзора.

Секторный обзор осуществляется путем механического или электрического качания луча антенны радиолокатора в пределах заданного сектора азимутального или угломестного обзора. В этом случае при постоянной угловой скорости обзора

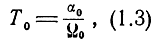
где α₀ - сектор обзора.

Винтовой обзор достигается путем кругового движения антенны радиолокатора по азимуту и медленного качания по углу места. В результате такого движения антенны луч описывает в пространстве винтовую линию (рис. 1.17). Такой вид обзора используется в режиме поиска целей в наземных и корабельных радиолокаторах орудийной наводки.

При винтовом обзоре

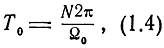
где N - число витков обзора.

Значение N выбирается из условия облучения каждой точки пространства в пределах области обзора, т. е.

где β₀ - угломестный сектор обзора,

θ_β - ширина диаграммы направленности в угломестной плоскости на уровне 0,5 по мощности.

Строчный обзор достигается путем быстрого качания луча антенны радиолокатора по азимуту и медленного качания по углу места. В результате луч описывает в пространстве зигзагообразную линию (рис. 1.18). Такой вид обзора используется в тех же случаях, что и винтовой.

При строчном обзоре

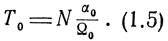
Из приведенных формул видно, что для уменьшения времени обзора необходимо увеличивать угловую скорость обзора. Однако существует верхний предел величины Ω₀, определяемый условиями обнаружения целей. В настоящее время, как правило, применяется такой режим обзора, при котором время облучения цели в течение одного периода обзора значительно превышает время максимального запаздывания отраженного сигнала.

Если реальную форму диаграммы направленности заменить сектором с углом θ, равным ширине диаграммы на уровне 0,5 по мощности, то время существования сигнала от цели, находящейся на расстоянии R, будет

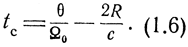
Как видим, время существования сигнала зависит не только от θ и Ω₀, но и от R, причем минимальное время существования сигнала будет при R = R_макс.

Пусть минимально допустимое время существования сигнала равно t_{с мин}. Тогда для обнаружения цели необходимо выполнить условие t_c ≥ t_{c мин}. Следовательно,

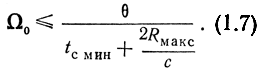
Значение t_{c мин} зависит от метода обнаружения и метода обработки отраженного сигнала. Так при импульсном методе обнаружения обычно принимают

где Т_п - период повторения импульсов.

Для радиолокаторов с непрерывным излучением значение t_{c мин}, как правило, больше, чем для импульсных радиолокаторов.

По количеству определяемых координат радиолокаторы делятся на одно-, двух- и трехкоординатные.

Примером однокоординатных радиолокаторов могут служить радиолокационные дальномеры и высотомеры. Двухкоординатные радиолокаторы позволяют определять либо дальность и азимут, либо дальность и угол места. Трехкоординатные радиолокаторы позволяют определять все три координаты, характеризующие местоположение цели в пространстве, т. е. дальность, азимут и угол места.

Точность определения координат цели характеризуется величинами систематических и случайных ошибок, возникающих при измерении дальности, азимута и угла места.

Под систематическими ошибками понимают такие, которые обусловливаются причинами, действующими вполне определенным образом. Так, например, задержка отраженного сигнала в приемнике вызывает систематическую ошибку дальности, а угловое смещение азимутального лимба радиолокатора вызывает систематическую ошибку азимута.

Систематические ошибки могут быть определены расчетным путем или экспериментально при помощи более точных методов и, следовательно, могут быть либо устранены, либо учтены в виде поправочных графиков, таблиц и т. п. Поэтому условимся в дальнейшем под результатом измерения понимать величину, свободную от систематической ошибки.

Под случайными ошибками понимают такие, которые вызываются весьма большим числом отдельных причин, не поддающихся точному учету и действующих в каждом отдельном измерении различным образом. Поэтому результат любого индивидуального измерения является фактически случайной величиной и его невозможно заранее предсказать. Однако последовательность ряда измерений в целом обладает определенными свойствами. В частности при неизменных условиях опыта средние результаты достаточно большого числа отдельных измерений практически остаются постоянными, причем постоянство средних результатов имеет устойчивый характер.

Чтобы иметь достаточно полное представление о статистических закономерностях случайных величин, необходимо знать, во-первых, область значений случайной величины, и, во-вторых, вероятность возможных ее значений. С этой целью в теории вероятностей вводят понятие функции распределения вероятностей случайной величины, под которой понимают вероятность того, что случайная величина U примет значение, меньшее, чем действительное произвольное число х, т. е.

Функция распределения вероятностей F(x) иначе называется интегральным законом распределения или интегральной функцией распределения.

Производная функции распределения непрерывной случайной величины

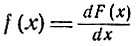
называется плотностью распределения вероятностей или дифференциальным законом распределения.

Вероятность того, что значение случайной величины будет лежать в пределах от х до х + dх, равна

Вероятность того, что значение случайной величины U не будет превосходить некоторого уровня х, равна

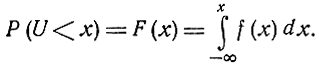
Функция распределения вероятностей или плотность распределения вероятностей дает наиболее полное представление о случайной величине. Однако в ряде случаев о случайной величине требуется иметь лишь некоторое суммарное представление. С этой целью в теории вероятностей применяют числовые характеристики случайных величин в виде начальных и центральных моментов распределения различных порядков.

Начальные моменты распределения k-го порядка определяются по формуле

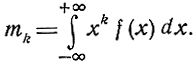
Начальный момент распределения первого порядка является математическим ожиданием или средним значением случайной величины U, т. е.

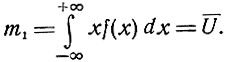
Центральные моменты распределения определяются по формуле

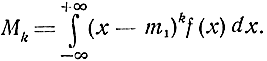
Центральный момент распределения первого порядка всегда равен нулю.

Центральный момент распределения второго порядка является математическим ожиданием квадрата отклонения случайной величины от ее среднего значения, т. е.

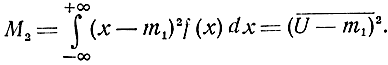
Момент М₂ называется дисперсией случайной величины.

Дисперсия дает представление о том, насколько сильно разбросаны значения случайной величины около ее среднего значения.

В теории вероятностей доказывается, что закон распределения суммы независимых случайных величин, при устремлении числа слагаемых к бесконечности и при ограниченной роли каждого из слагаемых стремится к нормальному закону распределения вне зависимости от законов распределения слагаемых (центральная предельная теорема теории вероятностей). Так как случайные ошибки, как правило, определяются большим числом факторов, из которых ни один не является доминирующим, то с достаточной для целей практики точностью можно считать, что случайные ошибки имеют нормальный закон распределения.

Плотность распределения вероятностей по нормальному закону имеет вид

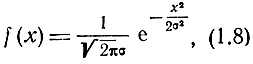
где σ² - дисперсия случайной ошибки.

Максимальная плотность вероятностей случайной ошибки при нормальном законе распределения будет при х = 0.

В теории ошибок в качестве числовой характеристики случайных ошибок принято считать среднюю квадратическую ошибку, которая равна корню квадратному из среднего значения квадрата случайной ошибки. При нормальном законе распределения случайных ошибок средняя квадратическая ошибка равна корню квадратному из дисперсии.

Для иллюстрации влияния величины средней квадратической ошибки на форму графика плотности нормального распределения вероятностей на рис. 1.19 представлено семейство кривых f(x), соответствующих различным значениям σ. Как видим, чем меньше средняя квадратическая ошибка, тем график f(x) имеет большее значение максимума и падает круче. Таким образом, уменьшению средней квадратической ошибки соответствует уменьшение вероятности больших ошибок. Следовательно, величина средней квадратической ошибки является характеристикой разбросанности значений случайных ошибок.

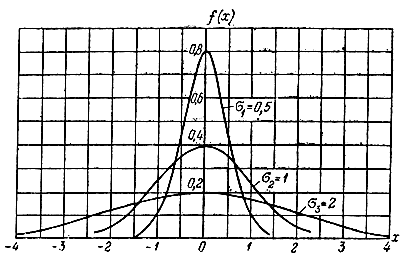
Рис. 1.19. Графики плотности распределения вероятностей по нормальному закону

Функция распределения вероятностей по нормальному закону имеет вид

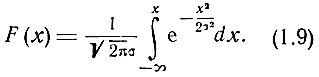
Семейство графиков F(x), соответствующих различным значениям σ, представлено на рис. 1.20.

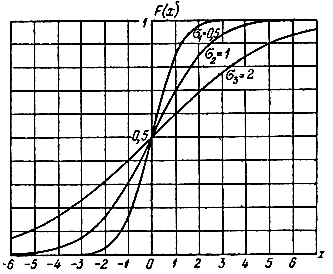
Рис. 1.20. Графики функции распределения вероятностей для нормального закона

Рассмотрим теперь, какова вероятность того, что случайная ошибка по абсолютной величине не превышает наперед заданной величины х. Поскольку функция f(x) является четной, то указанная вероятность равна

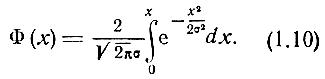
Функция Ф(х) является фактически другой формой записи функции распределения и называется интегралом вероятности. Таблицы функции 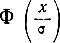можно найти в любом из многочисленных курсов по теории вероятностей. Так, Ф(1) = 0,6827, Ф(2) = 0,9545, Ф(3) = 0,9973. Это означает, что если выполнить большое число измерений (не менее двух-трех десятков), то примерно 70% ошибок по абсолютной величине не будет превосходить, σ, примерно 95% не будет превосходить 2σ и подавляющее большинство ошибок за редким исключением не будет превосходить 3σ.

Ошибку, равную 2σ, принято называть квазимаксимальной, а ошибку, равную 3σ, - максимальной. Следует иметь в виду, что приведенное определение максимальной ошибки является условным, так как ошибки, превосходящие по абсолютному значению 3σ, хотя и редко (теоретически в 0,27% случаев), но все же могут быть.

Кроме дисперсии σ² или средней квадратической ошибки σ, для характеристики точности измерений иногда применяются следующие величины:

1) средняя ошибка η, представляющая собой математическое ожидание абсолютной ошибки, т. е.

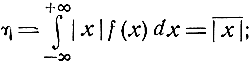
2) срединная или вероятная ошибка δ - такая величина, что вероятность ошибки, не превосходящей δ по абсолютной величине, равна ¹/₂, т. е.

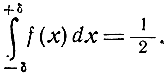
Все эти величины при нормальном законе распределения связаны между собой следующими соотношениями:

Средняя квадратическая ошибка по опытным данным вычисляется следующим образом. Пусть при измерении какой-либо величины U получено n ее значений с одинаковой степенью точности. В случае, когда ошибки измерения величины U подчиняются нормальному закону распределения, наиболее вероятным значением U будет среднее арифметическое

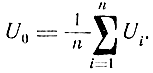
Затем определяются отклонения измеренного значения величины от среднего арифметического

Средняя квадратическая ошибка определяется по следующей формуле:

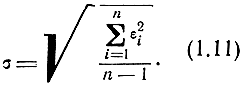
Средняя ошибка определяется по следующей формуле:

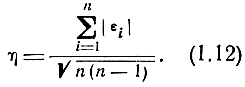
При нормальном законе распределения

Если же найденные значения отношений σ к η значительно отличаются от приведенного, то это свидетельствует о том, что в данном случае закон распределения вероятностей отличается от нормального.

Таковы основные характеристики точности определения координат.

На практике точность обычно характеризуют величиной срединной ошибки, что обычно специально не оговаривается. Если для характеристики точности используется другая величина, то, во избежание недоразумений, это должно быть оговорено.

Под разрешающей способностью радиолокатора понимают возможность раздельного определения координат близко расположенных целей. Различают разрешающие способности по дальности, азимуту, углу места и радиальной составляющей скорости цели.

Разрешающая способность по дальности δR характеризуется минимальным расстоянием между двумя целями с одинаковыми значениями α и β, при котором возможно раздельное определение дальности этих целей.

Разрешающая способность по азимуту δα характеризуется минимальной разностью азимутов двух целей с одинаковыми R и β, при которой возможно раздельное определение азимутов этих целей.

Разрешающая способность по углу места δβ характеризуется минимальной разностью углов двух целей с одинаковыми R и α, при которой возможно раздельное определение углов места этих целей.

Разрешающая способность по радиальной составляющей скорости цели δυ_r характеризуется минимальной разностью радиальных скоростей двух целей с одинаковыми значениями α и β, при которой возможно раздельное обнаружение и пеленгация этих целей.

Значение δR определяется методом дальнометрии, параметрами модуляции излучаемых колебаний и методом обработки принимаемых сигналов.

Значения δα и δβ определяются шириной луча радиолокатора в азимутальной и угломестной плоскостях.

Значение δυ_r определяется длительностью принятого сигнала и разрешающей способностью анализатора спектра выходного устройства радиолокатора.

Помехозащищенность радиолокатора характеризуется степенью его работоспособности в условиях наличия естественных и Искусственных, т. е. организованных, помех.

Основными техническими параметрами радиолокатора являются следующие: несущая частота, вид модуляции и ее параметры, мощность генератора высокой частоты, чувствительность приемника, диаграмма направленности антенны, число и типы выходных устройств.

Разумеется, что перечисленные здесь параметры радиолокатора не исчерпывают все их разнообразие. Так с точки зрения определения возможностей применения радиолокационной станции в заданных конкретных условиях представляют значительный интерес такие, например, параметры, как габариты и вес станции, ее работоспособность в заданных климатических условиях и условиях больших перегрузок и ряд других.