
2.2. Эффективная площадь рассеяния полуволнового вибратора
Эффективная площадь рассеяния полуволнового вибратора может быть найдена следующим путем.
Как известно, мощность, излучаемая вибратором
PΣ2 = I2RΣ,
где I - ток в пучности вибратора,
RΣ - сопротивление излучения вибратора.
В случае, когда полуволновый вибратор расположен параллельно вектору напряженности первичного электрического поля 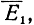
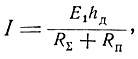
где hд - действующая высота вибратора,
Rп - сопротивление потерь вибратора.
Для ненагруженного вибратора Rп << RΣ, поэтому
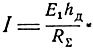
Тогда
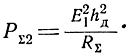
Из теории электромагнитного поля известно, что между плотностью потока энергии и напряженностью электрического поля существует следующая зависимость:
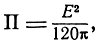
поэтому
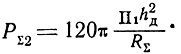
Подставляя найденное значение РΣ2 в формулу (2.6) и учитывая, что в рассматриваемом случае деполяризация отсутствует и, следовательно, ξ = 1, получаем
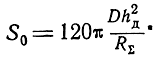
Так как для полуволнового вибратора 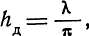 D = 1,64, RΣ = 73,3 ом, то
D = 1,64, RΣ = 73,3 ом, то
S0 = 0,86λ2. (2.7)
При произвольном расположении вибратора относительно вектора Е‾1 (рис. 2.1)
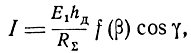
где γ - угол между меридиальной плоскостью вибратора и плоскостью поляризации вектора Е‾1,
β - угол между осью вибратора и составляющей вектора Е‾1 в меридиальной плоскости вибратора,
f(β) - диаграмма направленности вибратора в его меридиальной плоскости, равная
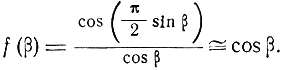
Тогда
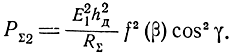
Подставляя это значение РΣ2 в формулу (2.6) и учитывая, что в рассматриваемом случае ξ = cos2 γ, D = 1,64f2(β), получаем
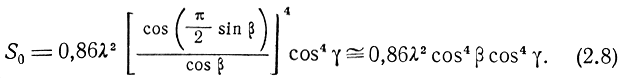
Из рис. 2.1 видно, что
cos β cos γ = cos θ,
где θ - угол между вектором E1 и осью вибратора. Поэтому
S0 ≅ 0,86 λ2 cos4 θ.
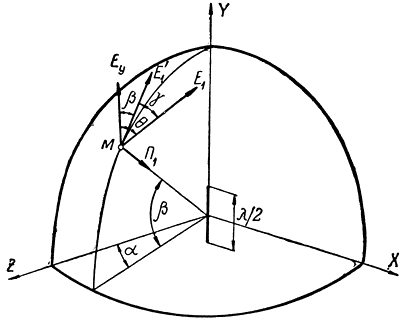
Рис. 2.1. К определению эффективной площади рассеяния полуволнового вибратора
Полуволновые вибраторы в виде бумажных металлизированных лент применяются в радиолокации для создания помех.
Определим среднее значение S0 в случае, когда любая ориентация вибратора в пространстве равновероятна.
В этом случае плотность распределения вероятностей угла θ будет
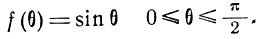
Следовательно, среднее значение эффективной площади рассеяния полуволнового вибратора будет
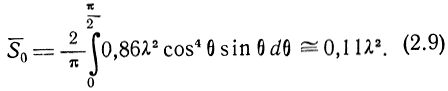

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
