2.3. Эффективная площадь рассеяния плоских поверхностей

Эффективная площадь рассеяния любой поверхности произвольной формы может быть найдена методом, подобным принципу Гюйгенса. Действительно, если распределение тока на поверхности известно, то, рассматривая каждый элемент поверхности как самостоятельный источник излучения, можно найти вторичное поле в точке приема путем суммирования полей элементарных источников с учетом фазовых соотношений.

Рассмотрим сущность этого метода на примере определения эффективной площади рассеяния гладкой идеально проводящей поверхности. В этом случае тангенциальная составляющая вектора электрического поля Е‾ и нормальная составляющая вектора магнитного поля Н‾ на поверхности равны нулю.

Поверхностная плотность тока, возбуждаемого первичным полем, на идеально проводящей плоскости, размеры которой значительно превышают длину волны, будет

где H₁ - напряженность магнитного поля падающей волны, n‾ - единичный вектор нормали к поверхности.

В векторной форме

Этой формулой можно воспользоваться и для расчета поверхностного тока на элементе криволинейной поверхности, если только его радиус кривизны значительно больше длины волны.

Вторичное поле в точке приема, создаваемое элементом поверхности, по которой течет ток, согласно теории элементарного вибратора, будет равно

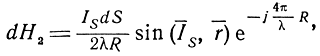
где r‾ - единичный вектор в направлении на радиолокатор,

R - расстояние между рассматриваемым элементом поверхности и точкой приема.

В векторной форме

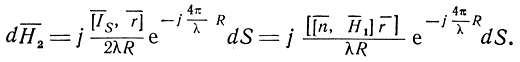
Двойное векторное произведение

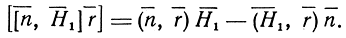
Поскольку вектор Н‾₁ лежит в плоскости, перпендикулярной направлению распространения, то

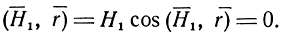
Поэтому

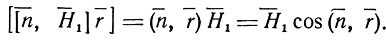
Тогда

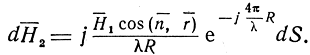
Следовательно,

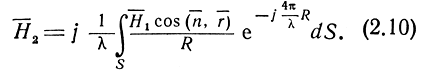
В случае, когда расстояние между радиолокатором и отражающей поверхностью достаточно велико по сравнению с ее размерами,

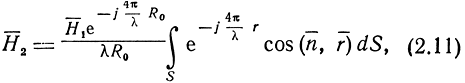
где r = R - R₀,

R₀ - расстояние от начала координат на отражающей поверхности до точки приема.

Из полученного выражения видно, что при оговоренных ранее условиях деполяризация вторичного поля отсутствует. Поэтому в соответствии с формулами (2.2) и (2.4)

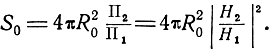
Так как модуль отношения

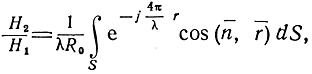
то

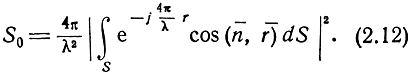
Если отражающая поверхность является плоской, то cos (n‾, r‾) = const.

Тогда

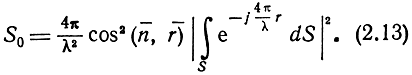
При нормальном падении на плоскую поверхность произвольной формы cos (n‾, r‾) = 1, а r = 0.

В этих условиях

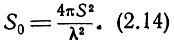
Определим теперь S₀ при наклонном падении.

Пусть отражающая поверхность представляет собой прямоугольную пластинку с размерами a и b (рис. 2.2).

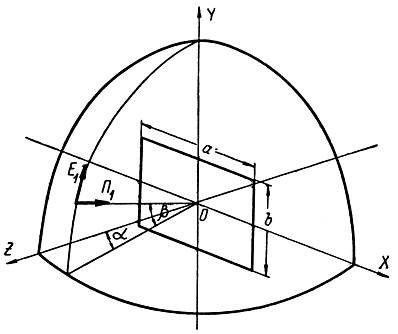
Рис. 2.2. К определению эффективной площади рассеяния прямоугольной пластинки

Если плоскость падения совпадает с плоскостью XOZ, то

Поэтому

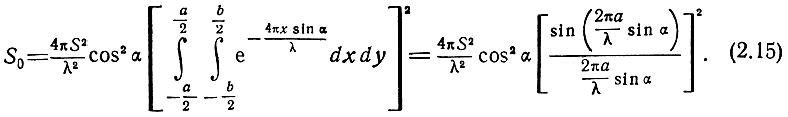
При небольших значениях угла падения α cos α ≅ 1, а sin α ≅ α.

В этих условиях

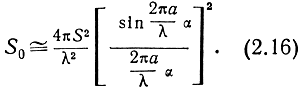
Если плоскость падения совпадает с плоскостью YOZ, то

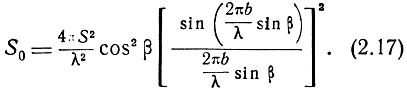
При cos β ≅ 1; sin β ≅ β;

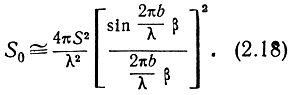
При произвольном расположении отражающей поверхности

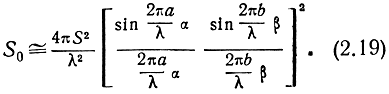
В случае, когда отражающая поверхность является круглым диском с диаметром, равным d,

где θ - угол падения,

ρ и φ - полярные координаты элемента поверхности dS, отсчитываемые от линии пересечения плоскости падения с плоскостью диска.

Тогда

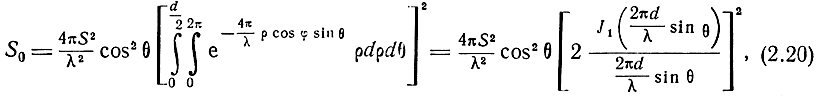
где J₁ - функция Бесселя первого порядка.

При cos θ ≅ 1; sin θ ≅ θ,

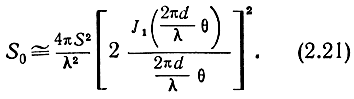
Из полученных формул видно, что зависимость эффективной площади рассеяния плоских поверхностей от угла падения носит осциллирующий характер. Это означает, что полярная диаграмма эффективной площади рассеяния будет иметь ряд лепестков (рис. 2.3). Ширина основного лепестка по нулевым значениям S₀ может быть найдена следующим путем. Согласно формуле (2.15) S₀ = 0 при

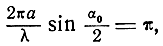
откуда

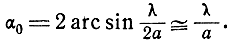
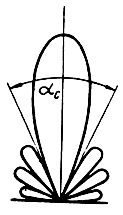
Рис. 2.3. Полярная диаграмма эффективной площади рассеяния пластинки

Аналогично из формулы (2.17) можно получить

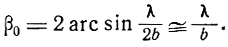
Из формулы (2.20) следует, что S₀ = 0 при

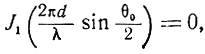
что будет при

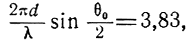
откуда

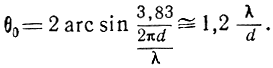
Ширина каждого из боковых лепестков уже основного примерно в два раза.

Таким образом, ширина лепестков определяется отношением линейных размеров отражающей поверхности к длине волны. Чем больше это отношение, тем уже лепестки.

Так, например, при 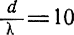ширина основного лепестка равна примерно 6°. Это означает, что изменение α от 0 до ±3° вызовет изменения S₀ от S_0макс до 0.