2.5. Эффективная площадь рассеяния множества целей

В том случае, когда радиолокатор одновременно облучает множество целей, на вход его приемника будет поступать такое же множество отраженных сигналов. Если селекция этих сигналов не возможна, то S₀, получаемое из формулы (2.5), является эффективной площадью рассеяния множества целей.

Рассмотрение эффективной площади рассеяния множества целей начнем с простейшего случая, когда радиолокатор одновременно облучает две цели, находящиеся настолько близко друг от друга, что разрешение их по дальности не возможно (рис. 2.8). В этом случае напряжение на входе приемника радиолокатора

где U_m1 и U_m2 - амплитуды входных напряжений от первой и второй целей;

φ₁ и φ₂ - запаздывания фаз этих напряжений, равные

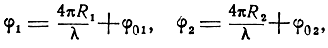
где φ₀₁ и φ₀₂ - изменения фаз при отражении.

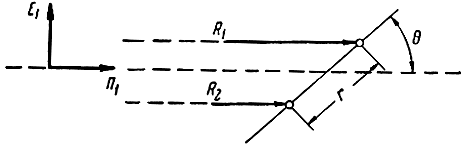
Рис. 2.8. К определению эффективной площади рассеяния двух близко расположенных целей

Если эффективные площади рассеяния целей равны между собой, то U_m1 = U_m2. Тогда

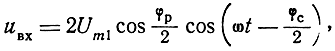
где φ_p и φ_с - разность и сумма фаз напряжений U₁ и U₂.

Из рис. 2.8 видно, что при φ₀₁ = φ₀₂

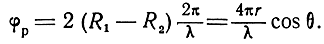
Поэтому амплитуда входного напряжения

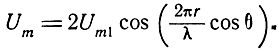
Соответственно суммарная мощность входного сигнала

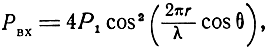
где Р₁ - мощность входного сигнала от одной цели.

Как видим, при изменении взаимного расположения целей в пространстве амплитуда входного напряжения будет также изменяться в пределах от 0 до 2U_m1, а мощность входного сигнала будет изменяться в пределах от 0 до 4Р₁.

Поскольку согласно формуле (2.5), между мощностью входного сигнала и эффективной площадью рассеяния существует линейная зависимость, то общая эффективная площадь рассеяния двух одинаковых целей будет

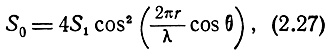
где S₁ - эффективная площадь рассеяния одной цели.

Таким образом, величина S₀ зависит не только от эффективной площади рассеяния каждой из целей, но и от их взаимного расположения. При изменении взаимного расположения целей величина S₀ будет меняться в пределах от 0 до 4S₁.

Среднее значение эффективной площади рассеяния двух целей при условии, что любое значение 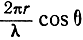от 0 до 2π равновероятно, будет

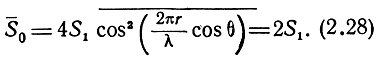
Перейдем теперь к случаю, когда напряжение на входе приемника является суммой напряжений от множества отдельных целей, т. е.

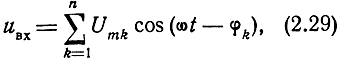
где U_mk - амплитуда входного напряжения от k-й цели,

φ_k - запаздывание фазы входного напряжения k-й цели.

Напряжение на входе приемника можно представить также в следующем виде:

где

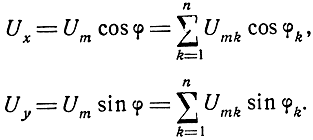
Амплитуда входного напряжения

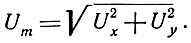
Если расположение целей в пространстве хаотически меняется, то хаотически изменяется и запаздывание фазы. В этих условиях составляющие амплитуды входного напряжения U_х и U_у будут величинами случайными.

Закон распределения напряжений U_х и U_у при большом числе целей и при ограниченной роли каждой из них, согласно центральной предельной теореме теории вероятностей, весьма близок к нормальному. В частном случае, когда амплитуды всех составляющих входного напряжения равны между собой, закон распределения напряжений U_х и U_у близок к нормальному уже при числе целей n ≥ 4÷5.

Итак,

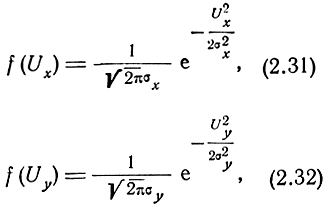
где σ_x² и σ_y² - дисперсии напряжений U_х и U_у.

В рассматриваемом случае

Поскольку случайные величины U_х и U_y являются независимыми, то двумерная плотность распределения

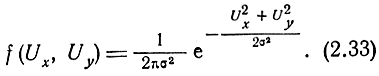
Для определения закона распределения амплитуды входного сигнала перейдем от декартовой системы координат к полярной. С этой целью выполним преобразование переменных в выражении (2.33) по известной из теории вероятностей формуле

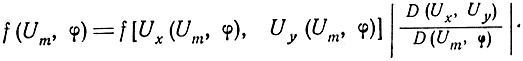
Так как

а модуль якобиана

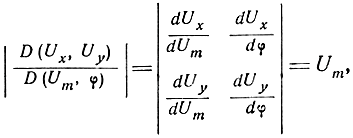
то

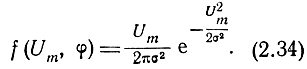
Следовательно,

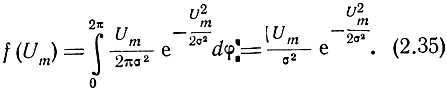
Как видим, плотность распределения вероятностей амплитуды входного напряжения описывается законом Релея.

Функция распределения амплитуды входного напряжения будет

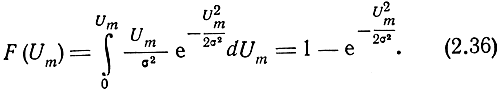
Графики плотности распределения вероятностей и функции распределения вероятностей по закону Релея приведены на рис. 2.9 и 2.10.

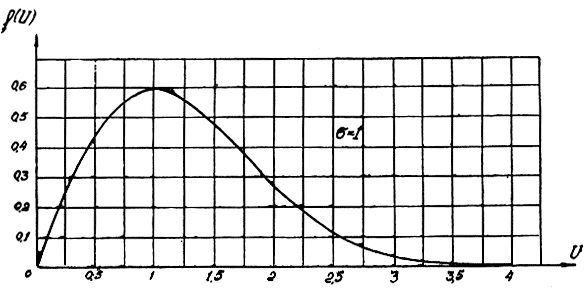
Рис. 2.9. График плотности распределения вероятностей по релеевскому закону

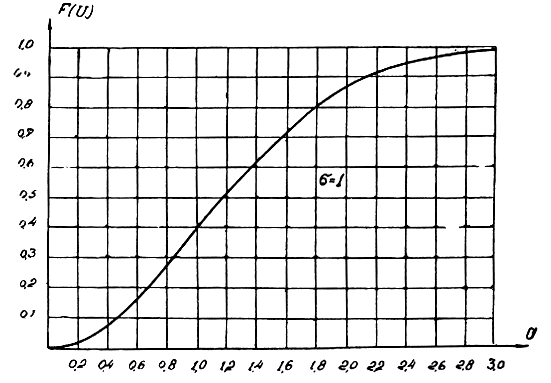
Рис. 2.10. График функции распределения вероятностей по релеевскому закону

Плотность распределения вероятностей мощности входного сигнала можно найти путем преобразования переменных в выражении (2.35) по известной из теории вероятностей формуле

Так как

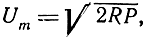
где R - входное сопротивление приемника, то

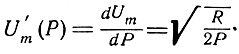
Поэтому

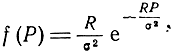
Подставив значение

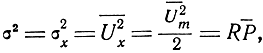
получим

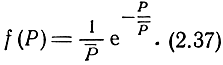
Функция распределения вероятностей мощности входного сигнала

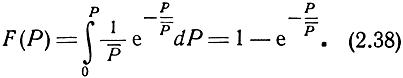
Соответственно плотность распределения вероятностей и функция распределения вероятностей эффективной площади рассеяния множества целей будут

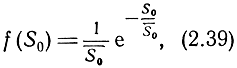
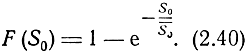
Графики f(S₀) и F(S₀) представлены на рис. 2.11 и 2.12.

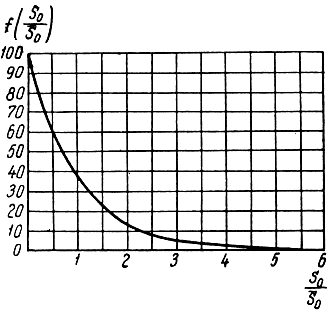
Рис. 2.11. График плотности распределения вероятностей эффективной площади рассеяния множества целей

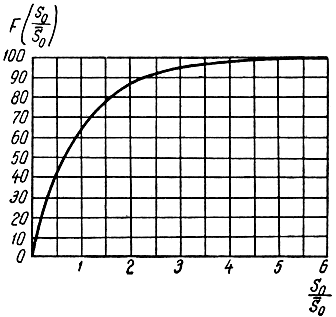
Рис. 2.12. График функции распределения вероятностей эффективной площади рассеяния множества целей

Таким образом, эффективная площадь рассеяния множества целей, взаимное расположение которых в пространстве с течением времени хаотически меняется, является случайной функцией времени; причем плотность распределения вероятностей и функция распределения вероятностей S₀ при оговоренных ранее условиях описываются экспоненциальным законом. Наиболее вероятное значение S₀ равно нулю. В течение 37% времени наблюдения S₀ превышает S‾₀ и только в течение 14% времени наблюдения S₀ превышает 2S‾₀.

Срединное значение S₀ равно