3.14. Динамические свойства радиодальномера с одним интегратором

Эквивалентная схема временного дискриминатора и блока управления с одним интегратором представлена на рис. 3.48. Здесь временной дискриминатор заменен генератором биполярных импульсов тока и ключом, периодически замыкаемым на время, равное длительности сигнала с выхода дискриминатора. Блок управления заменен эквивалентными сопротивлением R и емкостью C интегратора. Эта схема справедлива для случая, когда сопротивление, шунтирующее емкость интегратора, настолько велико, что его влиянием на работу схемы можно пренебречь.

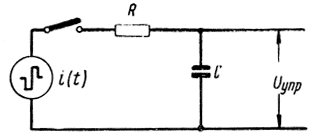
Рис. 3.48. Эквивалентная схема временного дискриминатора и блока управления с одним интегратором

Характерной особенностью рассматриваемой схемы является то, что изменение управляющего напряжения происходит лишь на протяжении малой части периода регулирования, равной длительности сигнала с выхода дискриминатора.

В целях упрощения анализа будем считать, что импульсы тока сигнала дискриминатора имеют прямоугольную форму и одинаковые амплитуды, равные I, а характеристика временного модулятора является линейной.

Тогда изменение управляющего напряжения в конце n-го периода регулирования будет

где 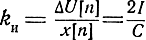- коэффициент преобразования интегратора.

Это изменение управляющего напряжения вызовет изменение интервала времени t_M на величину

где 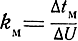- коэффициент преобразования временного модулятора.

Поэтому

Откуда с учетом формулы (3.54)

где k = k_Mk_и - коэффициент усиления системы.

Как видим, линейная импульсная система автоматического сопровождения по дальности с одним интегратором описывается линейным разностным уравнением первого порядка с постоянными коэффициентами.

Известно, что любая импульсная система регулирования в зависимости от ее параметров может быть как устойчивой, так и неустойчивой. В устойчивой системе при возрастании n временное рассогласование уменьшается, а в неустойчивой системе - наоборот увеличивается.

В теории автоматического регулирования доказывается, что необходимым и достаточным условием устойчивости для импульсной системы автоматического регулирования является соблюдение неравенства

где z_i - корни характеристического уравнения.

Для рассматриваемой системы характеристическое уравнение имеет вид

Следовательно, система будет устойчивой при

Рассмотрим теперь поведение системы при t_R = const. Для этого случая решение уравнения (3.57) примет вид

где x[0] - начальное временное рассогласование.

В устойчивой системе

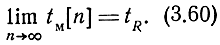
Следовательно, в установившемся режиме временное рассогласование будет равно нулю.

Характер переходного процесса определяется параметрами системы. Из уравнения (3.59) видно, что в устойчивой системе возможны два вида переходных процессов - апериодический при 0 < k < 1 (рис. 3.49, а) и колебательный затухающий при 1 < k < 2 (рис. 3.49, в). При k > 2 переходный процесс будет колебательным расходящимся. Такой вид неустойчивости возникает вследствие перерегулирования и является характерным для импульсных следящих систем.

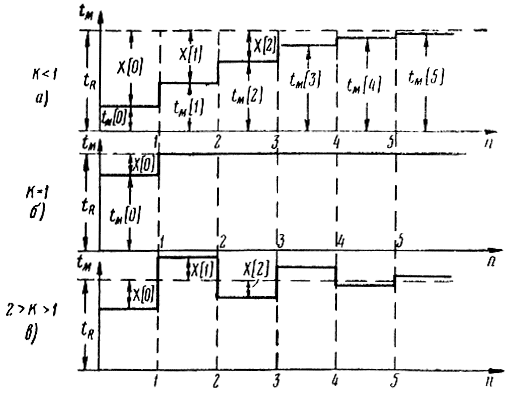
Рис. 3.49. Переходные процессы в системе автоматического сопровождения по дальности с одним интегратором

Быстродействие системы определяется величиной k. При k = 1 система отрабатывает любое допустимое рассогласование в течение первого периода регулировании (рис. 3.49, б). При увеличении или уменьшении k быстродействие системы ухудшается.

Напомним, что полученные результаты справедливы только при оговоренных ранее условиях, т. е. при равенстве амплитуд импульсов тока сигнала дискриминатора.

Если, например, сигнал на выходе временного дискриминатора представляет собой два сопряженных импульса напряжения прямоугольной формы с одинаковыми амплитудами, равными E, то при τ << RC

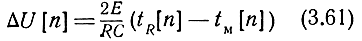
В этом случае изменение управляющего напряжения зависит не только от временного рассогласования, но и от величины управляющего напряжения. Последнее объясняется тем, что токи заряда и разряда емкости интегратора не равны между собой.

В рассматриваемом случае система описывается следующим разностным уравнением:

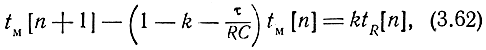
где

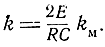
Условия устойчивости примут вид

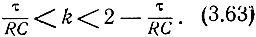
Необходимо, однако, иметь в виду, что поскольку обычно τ << RC, то условие (3.63) мало отличается от условия (3.58). Решение уравнения (3.62) при t_R = const примет вид

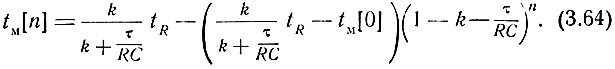
Для устойчивой системы

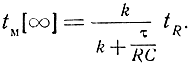
Как видим, в установившемся режиме t_M ≠ t_R, причем временное рассогласование равно

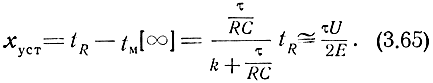
Из формулы (3.65) следует, что для уменьшения ошибки сопровождения необходимо уменьшать длительность импульса и величину управляющего напряжения и увеличивать амплитуду сигнала с выхода дискриминатора.

Рассмотрим теперь поведение системы в динамическом режиме, т. е. при сопровождении движущейся цели.

Пусть цель приближается к радиолокатору с постоянной скоростью υ_r.

Так как Т_р ≅ Т_п, то

где t_R[0] - значение t_R в момент начала сопровождения,

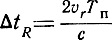
- изменение t_R за период повторения,

c - скорость распространения радиоволн.

Решение уравнения (3.57) в этом случае примет вид

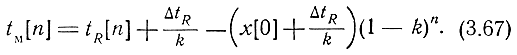
Временное рассогласование в установившемся режиме

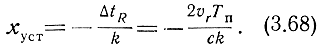
Следовательно, динамическая дальномерная ошибка сопровождения будет

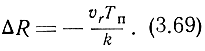
Как видим, уменьшение динамической дальномерной ошибки сопровождения может быть достигнуто путем уменьшения периода повторения и увеличения коэффициента усиления системы. Однако не следует упускать из виду, что уменьшение Т_п лимитируется условием однозначности дальнометрии, а увеличение k лимитируется условием устойчивости системы. Кроме того, при k → 2 ухудшается быстродействие системы.

Рассмотрим теперь поведение системы при полном пропадании отраженного сигнала. В этом случае при отсутствии сопротивления R_ш, шунтирующего емкость интегратора С, система сохраняет последнее отработанное значение управляющего напряжения сколь угодно долго. Следовательно, система обладает "памятью" по положению.

Наличие R_ш ограничивает время "памяти" по положению. Поэтому должны быть приняты меры, обеспечивающие увеличение постоянной времени CR_ш.

С этой целью обычно в блоке управления используют ламповый интегратор, одна из возможных схем которого представлена на рис. 3.50.

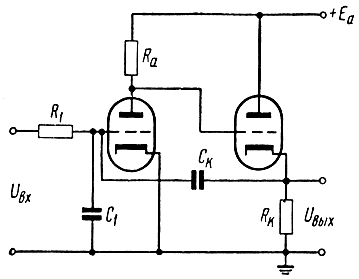
Рис. 3.50. Схема лампового интегратора

Эквивалентная емкость такого интегратора будет равна

C = C₁ + (1 + k₁⋅k₂)C_к,

где k₁ - коэффициент усиления первого каскада,

k₂ - коэффициент усиления второго каскада.

При сопровождении движущейся цели "память" по положению приносит пользу только в том случае, когда за время отсутствия сигнала отраженный импульс не успеет выйти за пределы селекторных импульсов. Это обстоятельство заставляет увеличивать длительность селекторных импульсов, что, естественно, ведет к ухудшению разрешающей способности по дальности.