3.15. Динамические свойства радиодальномера с двумя интеграторами

Одна из возможных схем блока управления с двумя интеграторами представлена на рис. 3.51.

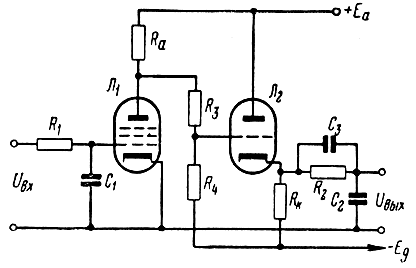
Рис. 3.51. Схема блока управления с двумя интеграторами

Здесь цепочка R₁C₁ является первым, а цепочка R₂C₂ - вторым интегратором. Емкость С₃ является стабилизирующим звеном. Разделительный усилитель на лампах Л₁ и Л₂ играет вспомогательную роль и позволяет, во-первых, устранить реакцию второго интегратора на первый, что повышает четкость работы схемы, и, во-вторых, увеличить чувствительность блока управления.

На рис. 3.52 представлена эквивалентная схема временного дискриминатора и блока управления, а на рис. 3.53 - идеализированные графики напряжений, поясняющие работу схемы.

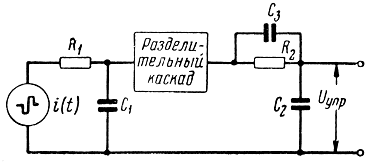
Рис. 3.52. Эквивалентная схема временного дискриминатора и блока управления с двумя интеграторами

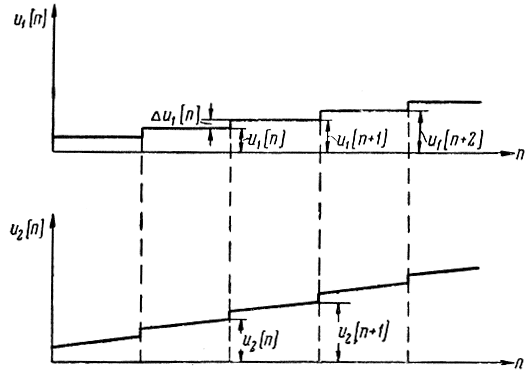
Рис. 3.53. Графики напряжений, поясняющие работу блока управления с двумя интеграторами

Характерной особенностью работы блока управления с двумя интеграторами является то, что управляющее напряжение изменяется в течение всего периода регулирования.

При выводе уравнений динамики системы будем по-прежнему считать, что сигнал с выхода дискриминатора представляет собой два сопряженных импульса тока прямоугольной формы с одинаковыми амплитудами. Кроме того, будем считать, что коэффициент усиления k_y разделительного усилителя не зависит от частоты. Последнее условие не нарушает общности выводов, если только разделительный усилитель не искажает существенно формы выходного напряжения первого интегратора.

При оговоренных условиях

где k_y - коэффициент усиления разделительного усилителя,

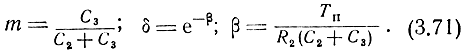
Аналогично

Исключая из уравнения (3.70) и (3.71) U₁[n + 1] путем совместного их решения и учитывая, что

где k_и - коэффициент преобразования первого интегратора, получаем

где k = k_иk_мk_у.

Таким образом, система автоматического сопровождения по дальности с двумя интеграторами описывается разностным уравнением второго порядка. Характеристическое уравнение системы

В теории автоматического регулирования доказывается, что условия устойчивости системы |z_i| < 1 можно выразить через коэффициенты характеристического уравнения.

Так, если характеристическое уравнение второго порядка, т. е.

то условия устойчивости системы сводятся к выполнению следующих неравенств:

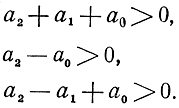
Эти неравенства для рассматриваемой системы примут вид

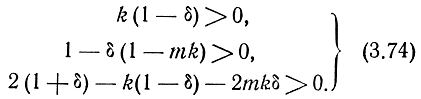
Поскольку k > 0, m > 0, а δ < 1, то первые два условия выполняются всегда. Поэтому единственным условием устойчивости системы является третье условие, которое при β << 1 можно представить в более простом виде

Характер переходного процесса в устойчивой системе определяется параметрами системы и может быть как апериодическим, так и колебательным затухающим, причем частота колебаний лежит в пределах от 0 до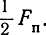

Длительность переходного процесса также определяется параметрами системы. При β << 1 наименьшая длительность переходного процесса, равная 2Т_п, будет при kβ = mk = 1. При увеличении или уменьшении значений kβ и mk длительность переходного процесса будет возрастать.

Рассмотрим теперь поведение системы при t_R = const. В этом случае решение уравнения (3.72) примет вид

где с₁ и с₂ - постоянные коэффициенты, определяемые параметрами системы и начальными условиями;

z₁ и z₂ - корни характеристического уравнения.

В устойчивой системе

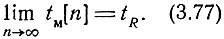
Следовательно, в установившемся режиме временное рассогласование равно нулю.

При сопровождении цели, приближающейся к радиолокатору с постоянной скоростью, решение уравнения (3.72) для установившегося режима примет вид

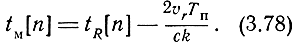
Следовательно, динамическая дальномерная ошибка сопровождения будет

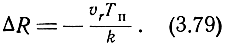
Существенно, что в системе с двумя интеграторами величина коэффициента k может быть значительно больше двух, поэтому ошибка сопровождения в этой системе будет много меньше, чем в системе с одним интегратором [формула (3.69)].

Рассмотрим теперь поведение системы при полном пропадании отраженного сигнала. В этом случае сигнал с выхода дискриминатора отсутствует, в силу чего k_и = 0. Тогда уравнение (3.72) примет вид

или

где Δt_M - изменение интервала времени t_M за один период повторения.

Решая уравнение (3.80), получаем

где Δt_M[0] - изменение интервала времени t_M за один период повторения в момент пропадания отраженного сигнала.

Так как Δt_M[0] пропорционально скорости цели, то, следовательно, система обладает "памятью" по скорости. Из уравнения (3.81) видно, что с увеличением постоянной времени второго интегратора продолжительность "памяти" по скорости возрастает.

Наличие "памяти" по скорости приводит к тому, что при временном пропадании отраженного сигнала автоматическое сопровождение цели по дальности не нарушается. При этом в отличие от системы с одним интегратором нет необходимости увеличивать длительность селекторных импульсов. Поэтому сопровождение цели в рассматриваемых условиях возможно без ухудшения разрешающей способности по дальности.