Глава пятая. Обнаружение радиолокационных сигналов

5.1. Выделение радиолокационных сигналов на фоне случайных помех

В самом начале курса указывалось, что задача обнаружения какой-либо цели при помощи радиоволн сводится к задаче обнаружения отраженного этой целью сигнала на фоне различного рода помех. В диапазоне УКВ основными видами естественных помех являются тепловые шумы, космические шумы, внутренние шумы приемника и шумы передатчика.

Тепловые шумы возникают вследствие теплового излучения объектов, окружающих приемную антенну радиолокатора. Спектр этих шумов, являясь практически равномерным вплоть до частот порядка 10¹³ гц, далеко выходит за пределы того диапазона частот, который используется в радиолокации. Поэтому такой шум называется "белым шумам" - по аналогии со световыми колебаниями, имеющими широкий спектр.

Космические шумы зарождаются в Галактике. Спектр этих шумов также весьма широкий. Интенсивность космических шумов по диапазону не постоянна. С повышением частоты уровень космических шумов уменьшается и на частотах выше 200-300 Мгц этими шумами можно пренебречь по сравнению с другими видами помех.

Внутренние шумы приемника возникают вследствие флюктуации электронного тока в лампах и электрических флюктуаций, связанных с тепловым движением электронов в электрических проводниках. Спектр этих шумов также весьма широкий.

Шумы передатчика возникают вследствие флюктуации электронного тока генераторных ламп. Спектр этих шумов также весьма широк, хотя и не равномерен. Наибольшая спектральная плотность шумов имеет место на частоте генератора. По мере ухода от частоты генератора спектральная плотность шумов уменьшается сначала быстро, а затем медленно. Шумы передатчика поступают на вход приемника вследствие несовершенства развязки передающего и приемного каналов радиолокатора.

При импульсном методе радиолокации шумы передатчика имеются на входе приемника только в период генерирования зондирующего импульса. В остальное время они отсутствуют и, следовательно, не влияют на условия обнаружения радиолокационных сигналов. При непрерывном излучении шумы передатчика имеются на входе приемника все время, что при плохих шумовых свойствах генераторных ламп и плохой развязке передающего и приемного каналов радиолокатора существенно ухудшает условия обнаружения отраженных сигналов.

Таким образом, даже при отсутствии помех искусственного происхождения на входе приемника всегда имеются помехи случайного характера с весьма широким спектром. Поэтому для обнаружения радиолокационных сигналов необходимо прежде всего произвести первичную обработку радиолокационных сигналов, состоящую в выделении сигналов на фоне случайных помех. Эта операция выполняется приемником радиолокатора.

Выделенные радиолокационные сигналы поступают затем в выходное устройство радиолокатора, где осуществляется вторичная обработка сигналов, для последующего обнаружения цели (обработка по порогу) и определения местоположения целей (обработка по положению).

При первичной обработке радиолокационных сигналов, как правило, используют различия спектральных составов сигналов и шумов. Поскольку спектр радиолокационных сигналов значительно уже спектра шумов, то при помощи соответствующих фильтров можно существенно повысить отношение сигнал/шум.

Действительно, пусть на вход линейного фильтра с частотной характеристикой К(ω) поступает напряжение

где u_c1(t) - напряжение сигнала,

u_ш1(t) - напряжение шума.

Тогда на выходе фильтра будет напряжение

где u_c2(t) и u_ш2(t) - есть результат преобразования фильтром напряжении сигнала и шума.

Сигнал на выходе фильтра можно представить как

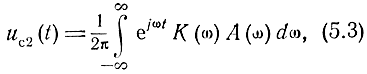
где А(ω) - спектр сигнала, равный

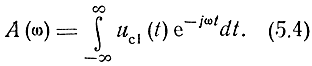
Среднее значение квадрата напряжения шума на выходе фильтра можно представить как

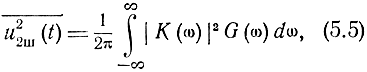
где G(ω) - спектральная плотность шума на входе фильтра.

Отношение мгновенной мощности сигнала к мощности шума в момент t₀ будет

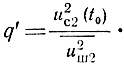
Учитывая формулы (5.3) и (5.5), получаем

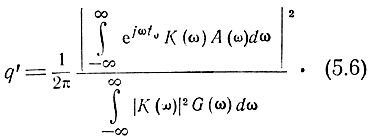
Найдем характеристику фильтра, при которой отношение сигнал/шум будет наибольшим.

Согласно неравенству Шварца-Буняковского

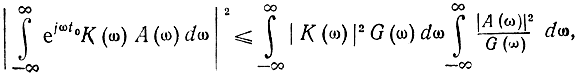
откуда

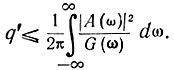
Если взять

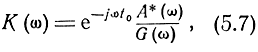
то отношение сигнал/шум в момент t₀ будет

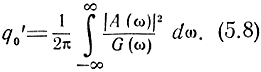
Как видим, в этом случае отношение сигнал/шум будет наибольшим. Следовательно, фильтр с частотной характеристикой (5.7) будет наилучшим. Такой фильтр называется согласованным или оптимальным. Можно показать, что если u_ш1(t) является нормальной случайной функцией, то фильтр с частотной характеристикой (5.7) является абсолютно оптимальным.

Физический смысл полученного результата заключается в том, что оптимальный линейный фильтр пропускает интервал частот от со до ω + dω в тем большей степени, чем больше спектральная амплитуда полезного сигнала и чем меньше спектральная плотность шума. Отношение сигнал/шум на выходе такого фильтра тем больше, чем больше спектр сигнала отличается от спектра шума.

Обычно спектр шума равномерно распределен по диапазону частот, занятому полезным сигналом, т. е.

где G - мощность шума, приходящаяся на полосу в 1 гц.

В этих условиях частотная характеристика оптимального фильтра с точностью до постоянного множителя равна

т. е. является комплексно сопряженной функцией спектра сигнала. Это означает, что форма частотной характеристики совпадает с формой частотного спектра сигнала.

Существенно, что при оговоренных условиях отношение сигнал/шум на выходе оптимального фильтра согласно формуле (5.8) равно

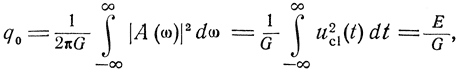
где E - энергия входного сигнала.

Мощность шума, отнесенная ко входу приемника (без учета космических шумов и шумов передатчика) можно представить как

где N - коэффициент шума приемника,

k - постоянная Больцмана,

Т - абсолютная температура,

Δf - эффективная полоса пропускания приемника, которую с достаточной для практики точностью можно считать равной полосе пропускания приемника на уровне 0,7 по напряжению.

Поэтому, при принятых пределах интегрирования в формуле (5.5),

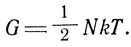
Тогда

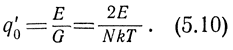
Так как

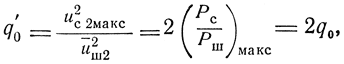
то

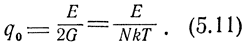
Как видим, при оптимальной фильтрации полезного сигнала на фоне белого шума отношение сигнал/шум определяется только энергией полезного сигнала на входе фильтра и спектральной плотностью шума, и совершенно не зависит от формы сигнала. Однако не следует упускать из виду, что форма сигнала решающим образом влияет на степень сложности выполнения оптимального фильтра. Для иллюстрации сказанного рассмотрим условия выделения одиночного высокочастотного импульса и пачки высокочастотных импульсов.

Спектр высокочастотного импульса прямоугольной формы с длительностью τ представлен на рис. 5.1. Форма частотной характеристики оптимального фильтра должна совпадать с формой этого спектра. Создание фильтра с такой характеристикой представляет собой довольно сложную техническую задачу, в решении которой, однако, нет большой необходимости. Так можно показать, что отношение сигнал/шум на выходе фильтра с прямоугольной частотной характеристикой равно

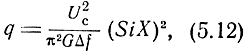
где U_c - амплитуда напряжения сигнала,

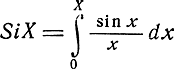
- интегральный синус,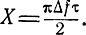

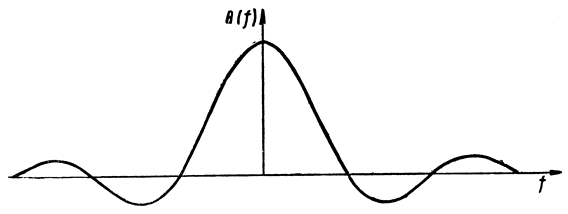
Рис. 5.1. Спектр высокочастотного импульса прямоугольной формы

Энергия прямоугольного импульса (при сопротивлении в 1 ом)

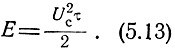
Тогда

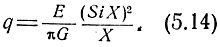
Так как для согласованного фильтра согласно формуле (5.11)

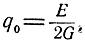
то

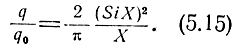
На рис. 5.2 изображена зависимость отношения 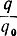от произведения τΔf.

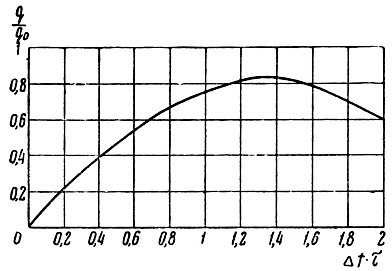
Рис. 5.2. Зависимость отношения сигнал/шум от произведения τΔf

Как видим, существует оптимальное значение произведения

при котором отношение 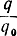будет максимальным. Иными словами, существует оптимальная ширина полосы пропускания рассматриваемого фильтра, равная

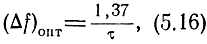
при которой

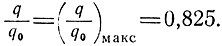
Следовательно, отношение сигнал/шум на выходе рассматриваемого фильтра при Δf = (Δf)_опт на 1 дб меньше, чем на выходе оптимального фильтра.

Реальная форма высокочастотного импульса, как известно, несколько отличается от прямоугольной, а реальная форма частотной характеристики приемника обычно значительно отличается от прямоугольной и больше приближается к оптимальной. Опытным путем установлено, что в этих условиях оптимальное значение полосы пропускания приемника, взятой на уровне 0,7 по напряжению, равно

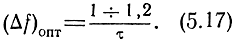
Физический смысл полученных результатов заключается в следующем.

Если взять Δf < (Δf)_опт, то мощность шума уменьшится, но еще сильнее уменьшится мощность сигнала, так как амплитуда напряжения не успеет за время существования импульса достигнуть установившегося значения. Поэтому отношение сигнал/шум ухудшится.

Если же взять Δf > (Δf)_опт, то мощность шума возрастет, а мощность сигнала останется неизменной, так как амплитуда напряжения сигнала достигнет установившегося значения за время, меньшее длительности импульса. Поэтому отношение сигнал/шум также ухудшится.

Таким образом, при правильном выборе полосы пропускания приемника, т. е. когда Δf = (Δf)_опт, условия выделения одиночного высокочастотного импульса на фоне белого шума весьма близки к оптимальным.

Рассмотрим теперь условия выделения сигнала, представляющего собой пачку из n когерентных высокочастотных импульсов, длительность каждого из которых τ и период повторения Т_п (рис. 5.3).

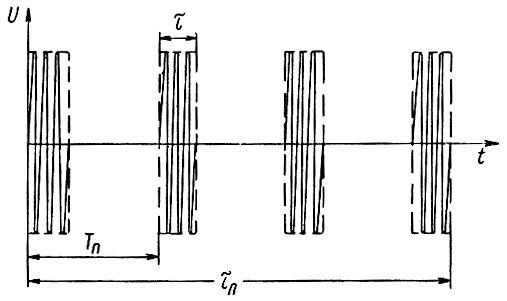
Рис. 5.3. Пачка высокочастотных импульсов

Спектр такого сигнала отличается от спектра одиночного высокочастотного импульса, и тем в большей степени, чем больше число импульсов в пачке.

На рис. 5.4 представлен спектр пачки когерентных высокочастотных импульсов при n = 19 и Т_п = 3τ. Энергия сигнала сосредотачивается около частот, кратных частоте повторения в полосах шириной порядка 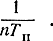В пределе при n → ∞ образуется дискретный спектр.

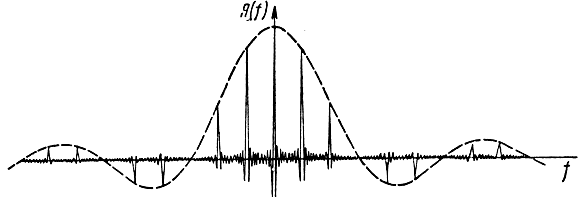
Рис. 5.4. Спектр пачки высокочастотных импульсов при n = 19 и Т_п = 3τ

Частотная характеристика фильтра оптимального для пачки высокочастотных импульсов должна иметь форму, напоминающую форму гребня (рис. 5.5)

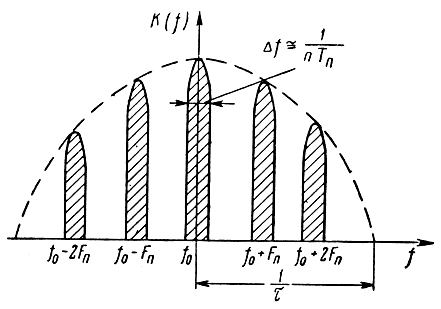
Рис. 5.5. Частотная характеристика фильтра, оптимального для пачки высокочастотных импульсов

Фильтр с такой характеристикой называется гребенчатым.

Гребенчатый фильтр можно выполнить из набора узкополосных фильтров, приближенно оптимальных для импульса длительностью, равной длительности всей пачки. Это означает, что полоса пропускания узкополосного фильтра должна выбираться из условия

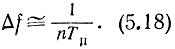
Огибающая частотных характеристик этих фильтров должна приближаться к частотной характеристике фильтра, оптимального для одного импульса пачки. Число узкополосных фильтров

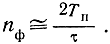
Выполненный таким путем гребенчатый фильтр обычно оказывается довольно громоздким. Так, например, гребенчатый фильтр, приближенно оптимальный для пачки из десяти высокочастотных импульсов, имеющих τ = 1 мксек и Т_п = 1000 мксек, должен состоять примерно из 2000 узкополосных фильтров с полосой пропускания порядка 100 гц. Разумеется, что такой фильтр выполнить довольно сложно.