5.2. Взаимодействие радиолокационных сигналов и шума

Для того чтобы иметь представление об условиях обнаружения радиолокационных сигналов в шумах, необходимо рассмотреть взаимодействие этих сигналов и шума.

Шум на входе приемника имеет, как уже указывалось, весьма широкий спектр. Поэтому он может иметь острые пики положительной и отрицательной полярностей и весьма малой длительности (порядка 10^-13 сек). Однако на выходе "линейной" части схемы приемника характер шумового напряжения приобретает вид почти синусоидального колебания с медленно меняющимися амплитудой и фазой, причем все параметры этого колебания: амплитуда, фаза и частота - являются случайными величинами. Если полоса пропускания приемника значительно меньше резонансной частоты, то разброс частоты шумового колебания будет не велик и наивероятнейшее значение частоты будет близко к резонансной. Амплитуда и фаза шумового колебания будут изменяться с частотой порядка Δf (рис. 5.6). Длительность выбросов огибающей шумового колебания также определяется полосой пропускания приемника и имеет порядок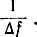

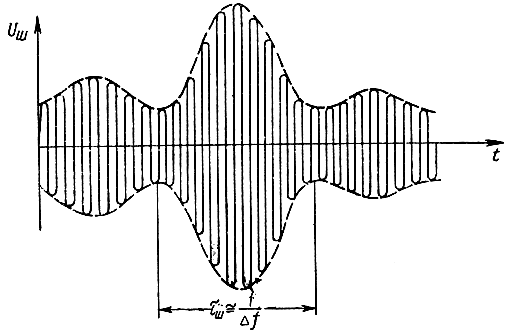
Рис. 5.6. Шумовое колебание на выходе линейной части приемника

Таким образом, шумовое напряжение на выходе линейной части схемы приемника можно представить, как

где амплитуда U_ш(t) и фаза φ(t) - случайные функции, ω₀ - резонансная частота.

Это напряжение можно представить в виде ортогональных составляющих (рис. 5.7) суммы двух

где

являются независимыми случайными величинами.

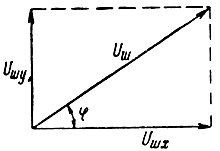
Рис. 5.7. Составляющие шумового напряжения

Поскольку составляющие U_шx и U_шy являются результатом сложения шумов от многих независимых источников, то в соответствии с предельной теоремой теории вероятностей эти составляющие распределены по нормальному закону

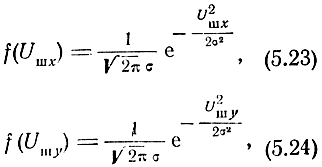
где 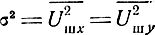- дисперсия шума.

Средние значения

При появлении сигнала

результирующее напряжение на выходе линейной части приемника, т. е. напряжение сигнал плюс шум (рис. 5.8), будет

где U_х = U_c + U_шx - случайная величина с нормальным законом распределения,

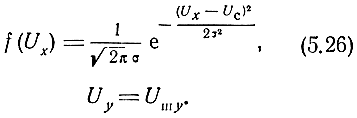
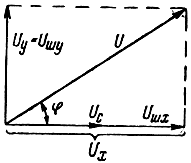
Рис. 5.8. Составляющие напряжений сигнала и шума

В этом случае средние значения

Результирующее напряжение u(t) можно представить также как

u(t) = U(t)cos [ω₀t + φ(t)], (5.27)

где

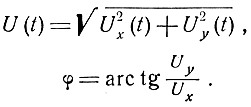
Найдем теперь закон распределения огибающей результирующего напряжения.

Так как случайные величины U_х и U_y являются независимыми, то двумерная плотность распределения

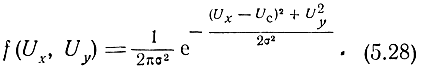
Перейдем от прямоугольной системы координат к полярной (рис. 5.8) по следующей формуле преобразования переменных:

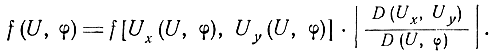
Так как

а модуль якобиана

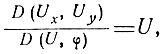
то

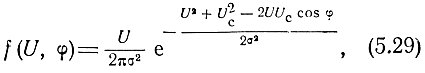
откуда плотность распределения вероятностей огибающей сигнала плюс шум будет

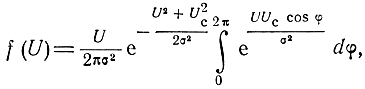
но

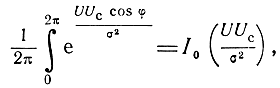
где 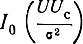- модифицированная функция Бесселя нулевого порядка.

Тогда

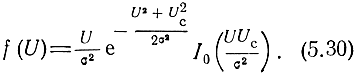
Это распределение называется обобщенным законом Релея.

В частном случае, когда U_c = 0

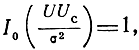
поэтому

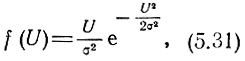
т. е. является релеевским законом распределения.

В другом частном случае, когда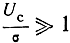

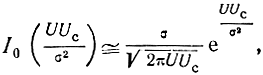
поэтому

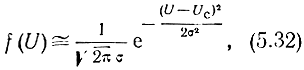
т. е. является нормальным законом распределения.

На рис. 5.9 представлены графики плотности распределения по обобщенному закону Релея, соответствующие различным значениям 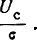Из этих графиков видно, что при увеличении интенсивности сигнала плотность распределения огибающей сигнала плюс шум от чисто релеевского переходит к чисто нормальному распределению.

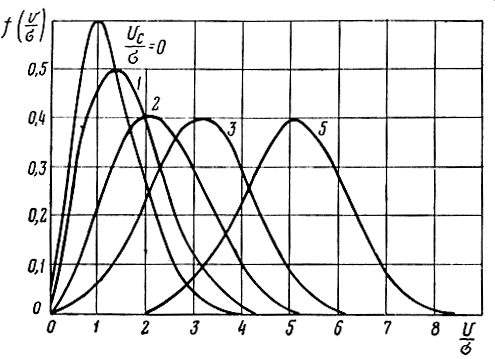
Рис. 5.9. Графики плотности распределения огибающей сигнала с шумом

Что касается плотности распределения фазы φ, то можно показать, что

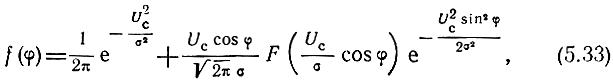
где

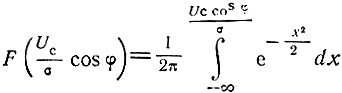
- функция Лапласа.

В частном случае, когда U_с = 0,

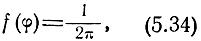
т. е. имеет место равномерное распределение фазы.

В другом частном случае, когда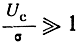

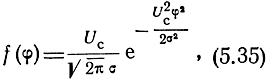
т. е. является нормальным законом распределения с дисперсией, равной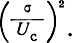

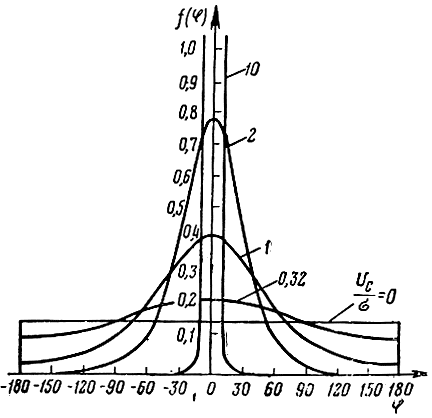
Рис. 5.10. Графики плотности распределения фазы сигнала с шумом

На рис. 5.10 представлены графики плотности распределения фазы сигнала плюс шум. Из этих графиков видно, что по мере роста отношения 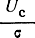плотность распределения f(φ) от равномерного приближается к нормальному закону распределения. В пределе при 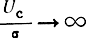плотность распределения f(φ) приближается к дельта-функции.