
5.3. Статистические критерии обнаружения радиолокационных сигналов
Выше неоднократно отмечалось, что на выходе приемника радиолокатора всегда имеются помехи случайного характера в виде напряжения шума. Эти помехи маскируют радиолокационные сигналы, и тем самым ухудшается их наблюдаемость. Поэтому результаты обнаружения радиолокационных сигналов на фоне шумов носят вероятностный характер и лишь только при достаточно большом превышении сигналом шумового фона эти результаты становятся практически достоверными. Следовательно, задача обнаружения радиолокационных сигналов в присутствии шумов является статистической задачей, так как определение наличия или отсутствия сигнала эквивалентно проверке справедливости гипотезы HS о наличии сигнала и шума в противовес альтернативной гипотезе H0 о наличии только одного шума.
Поскольку решение о наличии или отсутствии сигнала принимается на основании конечного количества информации, то возможны ошибочные решения в виде ложной тревоги, когда шум принимается за сигнал, и в виде пропуска сигнала, когда сигнал с шумом принимается за шум.
Для иллюстрации сказанного рассмотрим случай, когда решение о наличии или отсутствии сигнала принимает оператор на основании наблюдения одного хода развертки на индикаторе типа А (рис. 5.11). Пусть оператор считает, что если выброс на экране превышает некоторый уровень U0, то сигнал есть, а в противоположном случае сигнала нет. При таком правиле решения вероятность ложной тревоги будет равна (рис. 5.12).
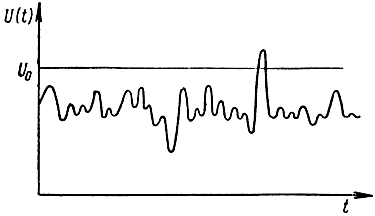
Рис. 5.11. Осциллограмма выходного напряжения на экране индикатора типа А
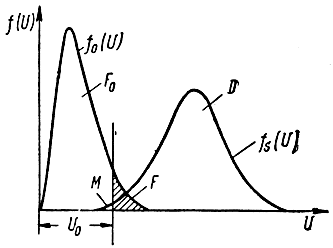
Рис. 5.12. Плотности распределения вероятностей огибающих шума и сигнала с шумом
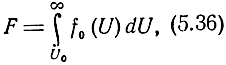
а вероятность пропуска сигнала будет равна
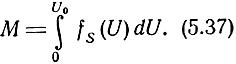
Здесь f0(U) и fs(U) - плотности распределения вероятностей огибающих шума и сигнала с шумом. При линейном детектировании f0(U) и fs(U) определяются выражениями (5.31) и (5.30).
Вероятность правильного обнаружения сигнала, равная вероятности превышения сигналом вместе с шумом уровня U0, будет (рис. 5.12)
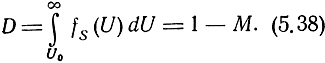
Вероятность правильного необнаружения сигнала, равная вероятности непревышения шумом уровня U0, будет (рис. 5.12)
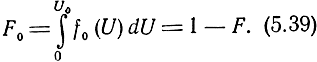
Таким образом, наблюдаемость радиолокационных сигналов характеризуется значениями вероятностей ложной тревоги и пропуска цели и чем эти вероятности меньше, тем наблюдаемость лучше.
Найдем теперь вероятности правильного принятия гипотез Нs и H0.
Из теории вероятностей известно, что вероятность наступления двух совместимых зависимых случайных событий А и В равна
Р(АВ) = Р(А) РА(В).
Здесь Р(A) - априорная вероятность события A, т. е. безусловная вероятность события A, вычисленная без учета того, произошло ли зависимое от него событие В. РА(В) - апостериорная вероятность события В, т. е. условная вероятность события В, вычисленная в предположении, что событие A произошло.
Пусть априорные вероятности наличия сигнала и его отсутствия соответственно равны P(S) и Р(0), причем
P(S) + P( 0) = 1. (5.40)
Тогда вероятность того, что гипотеза Hs принята правильно, будет равна
P(Hs) = Р(S) ⋅ D = P(S) ⋅ (1 - М), (5.41)
а вероятность того, что гипотеза H0 принята правильно, будет равна
Р(Н0) = Р(0) ⋅ F0 = Р(0) ⋅ (1 - F). (5.42)
Так как гипотезы Hs и Н0 являются несовместимыми, то на основании правила сложения вероятностей общая вероятность правильного решения
Рправ = Р(Нs) + Р(Н0).
Подставляя значения P(Hs) и P(H0) из формул (5.41) и (5.42), получаем
Pправ = P(S)(1 - M) + P(0)(1 - F). (5.43)
Вероятность неправильного решения
Рнеправ = 1 - Pправ (5.44)
или с учетом формул (5.40)
Рнеправ = P(S)M + P(0)F. (5.44а)
Как видим, вероятности правильного и неправильного решений зависят от значений априорных вероятностей наличия и отсутствия сигнала, а также от значений вероятностей ложной тревоги и пропуска сигнала.
Необходимо иметь в виду, что значения априорных вероятностей P(S) и Р(0), как правило, неизвестны. Поэтому вычисление вероятности правильного решения по формуле (5.43) не может быть выполнено.
Однако из этой формулы следует, что для увеличения вероятности правильного решения необходимо уменьшать вероятности ложной тревоги и пропуска сигнала.
В рассматриваемом примере уменьшение этих вероятностей может быть достигнуто только за счет увеличения отношения сигнал/шум, что наглядно иллюстрируется рис. 5.9. Ниже принято 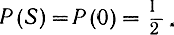
Перейдем теперь к рассмотрению общего случая, когда в результате наблюдений имеется дискретная выборка из n значений случайной величины U, полученная в интервале времени от 0 до Т.
Предположим, что случайная величина U имеет n-мерную плотность распределения вероятностей
fn(U1, U2, ..., Un/α),
где U1, U2, ..., Un - выборочные значения случайной величины U в интервале наблюдения Т,
α - параметр, характеризующий распределение (например, амплитуда сигнала, частота сигнала и т. п.).
Пусть при наличии сигнала α = S, а при отсутствии сигнала α = 0. Тогда соответствующие плотности распределения будут
fn(U1, U2, ..., Un/S),
и
fn(U1, U2, ..., Un/0).
Проверка гипотез Hs и H0 в рассматриваемом случае требует разделения n-мерного пространства наблюдений Г на две области Гs и Г0, первая из которых соответствует гипотезе Нs, а вторая - гипотезе Н0.
Тогда вероятность ложной тревоги
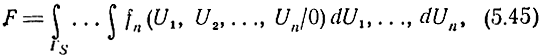
а вероятность пропуска сигнала при S = const
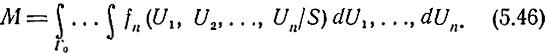
Если параметр α является случайной величиной, то
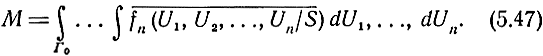
При разделении области Г на области Гs и Г0 можно пользоваться различными правилами, лишь бы они обеспечивали возможно большую вероятность правильного решения в заданных условиях. Так, решение о наличии сигнала можно принимать в соответствии с правилом, при котором при фиксированных значениях F и n вероятность пропуска сигнала сводится к минимуму.
Наблюдатель, использующий это правило, называется наблюдателем Неймана-Пирсона.
Решение о наличии сигнала при фиксированном времени наблюдения можно принимать и в соответствии с другим правилом, при котором сумма вероятностей пропуска сигнала и ложной тревоги сводится к минимуму. Наблюдатель, использующий это правило, называется идеальным наблюдателем или наблюдателем Зигерта.
Можно, наконец, n-мерное пространство испытаний разделить не на две, а на три области; Гs, Гпром и Г0. Области Гs и Г0, как и ранее, соответствуют гипотезам Нs и H0, а область Гпром является промежуточной.
Если совокупность наблюдений при фиксированных значениях F и М попадет в промежуточную область, то испытание продолжается до тех пор, пока эта совокупность не окажется в области Гs или Г0.
В этом случае величина выборки (величина n) является переменной. Наблюдатель, использующий это правило, называется последовательным наблюдателем или наблюдателем Вальда.
Все перечисленные правила обеспечивают наибольшую вероятность правильного решения и поэтому называются оптимальными.
Введем теперь следующее обозначение:
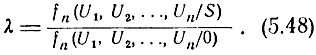
Величина λ называется коэффициентом правдоподобия.
Можно показать, что при наблюдателе Неймана-Пирсона области Гs и Г0 разделены поверхностью
λ = λпорог, (5.49)
где λпорог - пороговое значение коэффициента правдоподобия. Поэтому наблюдатель Неймана-Пирсона принимает одно из следующих решений:
λ > λпорог - сигнал есть,
λ < λпорог - сигнала нет.
Значение λпорог зависит от величины вероятности ложной тревоги.
При идеальном наблюдателе области Гs и Г0 разделены поверхностью
λ = 1. (5.50)
Поэтому идеальный наблюдатель принимает одно из дующих решений:
λ > λпорог - сигнал есть,
λ < λпорог - сигнала нет.
При последовательном анализе области Г0 и Гпром разделены поверхностью
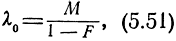
а области Гпром и Гs
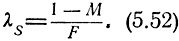
В этом случае испытание продолжается до тех пор, пока
λ0 < λ < λs.
Последовательный наблюдатель принимает одно из следующих решений:
λ > λs - сигнал есть,
λ < λ0 - сигнала нет.
Как видим, последовательные испытания являются двухпороговыми, в то время как первые два вида испытаний являются однопороговыми.
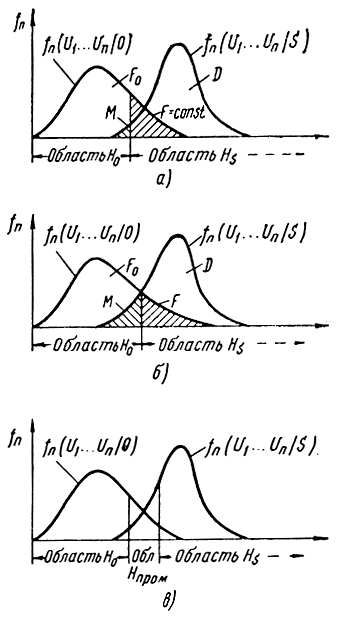
Рис. 5.13. Способы разделения области наблюдений при различных критериях обнаружения. а - наблюдатель Неймана-Пирсона, б - идеальный наблюдатель, в - последовательный наблюдатель
На рис. 5.13 представлены способы разделения области наблюдений при различных критериях обнаружения. Разумеется, этот рисунок носит схематический характер, так как в общем случае область наблюдения является я-мерной областью.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
