
5.4. Пороговая мощность радиолокационных сигналов
Под пороговой мощностью радиолокационных сигналов понимают ту их минимальную мощность на входе приемника радиолокатора, при которой обеспечиваются заданные вероятности правильного обнаружения цели и ложной тревоги.
Пороговая мощность радиолокационных сигналов, которую в дальнейшем для краткости будем называть просто пороговой мощностью, является одним из основных параметров радиолокатора, определяющим максимальную дальность радиообнаружения.
Величина пороговой мощности зависит от заданных значений вероятностей правильного обнаружения цели и ложной тревоги, параметров радиолокационных сигналов и помех, вида первичной и вторичной обработок радиолокационных сигналов и времени наблюдения.
Пусть на выходе линейной части приемника имеются n стробированных по дальности импульсов высокой частоты и помехи в виде белого шума. Если при этом полоса пропускания приемника согласована с длительностью импульса, то время корреляции огибающей шума будет значительно меньше периода повторения импульсов и, следовательно, корреляция между импульсами будет отсутствовать.
Тогда n-мерные плотности распределения вероятностей сигнала с шумом и шума в соответствии с формулами (5.30) и (5.31) будут
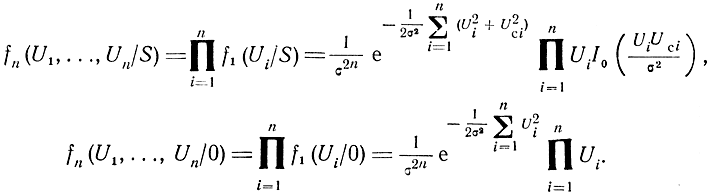
Следовательно, коэффициент правдоподобия согласно формуле (5.48) будет
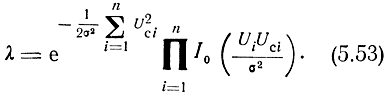
Допустим, что обнаружение радиолокационных сигналов выполняется по правилу Неймана-Пирсона, когда считается, что сигнал есть, если λ ≥ λпор. Это правило решения можно представить и в таком виде, как
ln λ ≥ ln λпор.
Подставляя значение λ из формулы (5.53), получаем
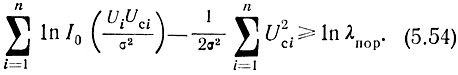
Такие же неравенства можно получить и для других наблюдателей.
Таким образом, оптимальная обработка пачки некогерентных импульсов сводится к оптимальной фильтрации каждого импульса, их детектированию и последетекторному интегрированию, причем оптимальной характеристикой детектора является логарифмическая характеристика.
Однако при слабом сигнале, т. е. при малом отношении сигнал/шум, логарифмическая характеристика весьма близка к квадратичной, так как при 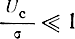
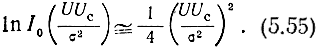
При сильном же сигнале, т. е. при большом отношении сигнал/шум, логарифмическая характеристика весьма близка к линейной, так как при Uc/σ >> 1
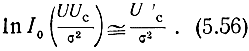
Поэтому линейный детектор при сильном сигнале практически весьма близок к оптимальному. Если при этом учесть, что в случае слабого сигнала линейный детектор ведет себя почти так же, как и квадратичный, то становится очевидным, что такой детектор весьма близок к оптимальному при любых значениях отношения сигнал/шум.
Наличие в неравенстве (5.54) слагаемого в виде 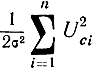 свидетельствует о том, что коэффициент передачи оптимального детектора зависит от энергии обнаруживаемого сигнала. Но можно показать, что эта зависимость не является существенной и обычный однополупериодный линейный детектор с постоянным коэффициентом передачи достаточно близок к оптимальному.
свидетельствует о том, что коэффициент передачи оптимального детектора зависит от энергии обнаруживаемого сигнала. Но можно показать, что эта зависимость не является существенной и обычный однополупериодный линейный детектор с постоянным коэффициентом передачи достаточно близок к оптимальному.
При вычислении вероятностей правильного обнаружения цели и ложной тревоги в общем виде наталкиваются на серьезные математические трудности. Однако в случае слабых сигналов, а этот случай и представляет наибольшую практическую ценность, указанные вероятности могут быть определены.
При слабом сигнале неравенство (5.54) с учетом формулы (5.55) можно представить как
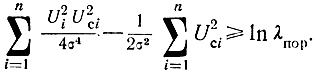
Для наиболее простого случая, когда амплитуда сигнала в пределах пачки импульсов постоянна, это неравенство приобретает вид
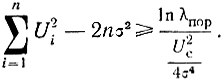
Если число интегрируемых видеоимпульсов n >> 1, то в соответствии с предельной теоремой теории вероятностей можно считать, что сумма независимых случайных величин U2i имеет нормальное распределение.
Можно показать, что в этом случае вероятности правильного обнаружения сигнала и ложной тревоги будут
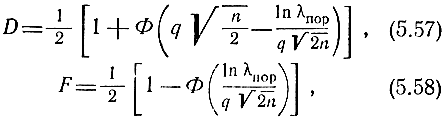
где 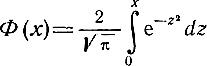 - интеграл вероятностей;
- интеграл вероятностей;
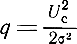
- отношение мощности сигнала к мощности шума на выходе линейной части приемника.
Как видим, вероятность правильного обнаружения при заданной вероятности ложной тревоги тем выше, чем больше отношение сигнал/шум на входе детектора и чем больше число интегрируемых импульсов.
Повышение вероятности правильного обнаружения при возрастании числа интегрируемых импульсов происходит вследствие синхронного накопления, поскольку, как указывалось выше, на выходе детектора суммируются импульсы, стробированные по дальности.
Формулы (5.57) и (5.58) позволяют построить графики зависимости вероятности правильного обнаружения цели при заданной вероятности ложной тревоги от величины отношения сигнал/шум и числа интегрируемых импульсов. Такие графики дают весьма наглядное представление о наблюдаемости радиолокационных сигналов и называются поэтому характеристиками обнаружения. На рис. 5.14 приведены характеристики обнаружения для наблюдателя Неймана-Пирсона в случае слабого сигнала с постоянной амплитудой. Характеристики обнаружения для других наблюдателей имеют примерно такой же вид.
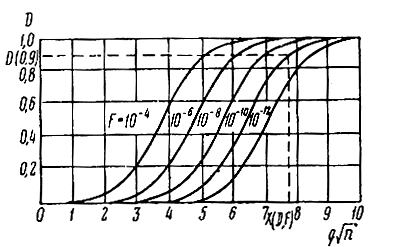
Рис. 5.14. Характеристики обнаружения для наблюдателя Неймана-Пирсона в случае слабого сигнала с постоянной амплитудой
Вид характеристик обнаружения флюктуирующего сигнала зависит от скорости флюктуаций. Так, в случае быстрых флюктуаций, когда импульсы в пачке можно считать некоррелированными, характеристики обнаружения при n > 10 практически такие же, как и при отсутствии флюктуаций. И только при n < 10 имеет место некоторое ухудшение наблюдаемости флюктуирующего сигнала.
Однако в случае медленных флюктуаций, когда импульсы в пачке являются жестко коррелированными, т. е. в случае дружно флюктуирующей пачки импульсов, характеристики обнаружения значительно отличаются от характеристик обнаружения сигналов с постоянной амплитудой. На рис. 5.15 приведены характеристики обнаружения для наблюдателя Неймана-Пирсона при F = 10-10 в случае слабого медленно флюктуирующего сигнала с релеевским распределением амплитуд (Сплошная кривая) и слабого нефлюктуирующего сигнала (пунктирная кривая). Здесь под q следует понимать среднее значение отношения сигнал/шум. Как видим, в области больших значений D(D > 0,5) наблюдаемость медленно флюктуирующих сигналов значительно хуже наблюдаемости нефлюктуирующих или быстро флюктуирующих сигналов.
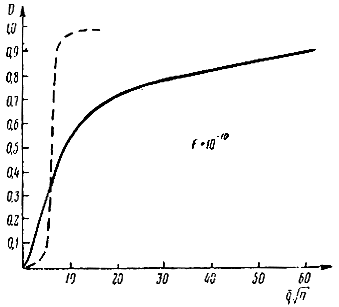
Рис. 5.15. Характеристики обнаружения для наблюдателя Неймана-Пирсона в случае слабого сигнала. ___ флюктуирующий сигнал, --- - сигнал с постоянной амплитудой
Располагая характеристиками обнаружения, можно найти то пороговое значение отношения qпор, при котором будут обеспечены заданные вероятности D и F. Для характеристик обнаружения, представленных на рис. 5.14,
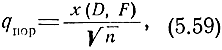
где x(D, F) - абсцисса той точки на характеристике, которая соответствует заданным вероятностям D и F.
При определении отношения qпор обычно задаются вероятностями D = 0,5 или D = 0,9 и F = 10-10. Такие значения вероятности D выбирают из следующих соображений.
Вероятности D < 0,5 с практической точки зрения не представляют значительного интереса, а при вероятностях D > 0,9 характеристики обнаружения становятся настолько пологими, что не представляется возможным определить значение qпор с необходимой точностью.
Выбор фиксированного значения вероятности F = 10-10 является условным, но следует иметь в виду, что изменение заданного значения F в широких пределах сравнительно слабо влияет на изменение qпор (рис. 5.14).
Отметим, что qпор пропорционально 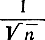 только при слабом сигнале. В случае же сильного сигнала qпор пропорционально
только при слабом сигнале. В случае же сильного сигнала qпор пропорционально 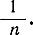 Сказанное объясняется тем, что детектирование слабого сигнала всегда является квадратичным, при котором происходит подавление слабого сигнала, более сильным шумом. В случае же сильного сигнала возможно линейное детектирование, при котором подавление сигнала шумом отсутствует.
Сказанное объясняется тем, что детектирование слабого сигнала всегда является квадратичным, при котором происходит подавление слабого сигнала, более сильным шумом. В случае же сильного сигнала возможно линейное детектирование, при котором подавление сигнала шумом отсутствует.
Поскольку при малом числе интегрируемых импульсов (n < 10), обеспечение вероятностей D порядка 0,5 и более возможно только при сильном сигнале, то qпор в этом случае пропорционально 1/n. Если же, наоборот, число интегрируемых импульсов велико (n > 100), то обеспечение тех же вероятностей правильного обнаружения цели возможно при слабом сигнале, вследствие чего qпор пропорционально 1/√n. В промежуточном случае, т. е. при 10 < n < 100, зависимость qпор от n будет более слабой чем 1/n, но более сильной чем 1/√n.
Для иллюстрации сказанного на рис. 5.16 приведены графики зависимости qпор от n для наблюдателя Неймана-Пирсона в случае сигнала с постоянной амплитудой при D = 0,9 и различных фиксированных значениях F.
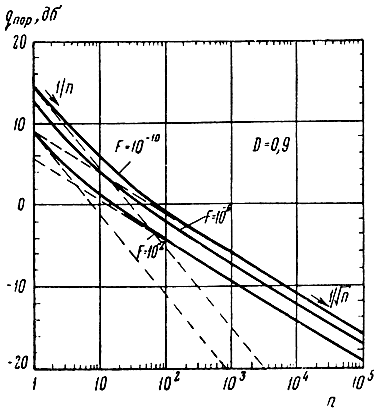
Рис. 5.16. Зависимость qпор от n для наблюдателя Неймана-Пирсона в случае сигнала с постоянной амплитудой
Перейдем теперь к определению пороговой мощности.
При оптимальной фильтрации высокочастотного импульса отношение сигнал/шум не зависит от числа импульсов в пачке и согласно формуле (5.11) равно
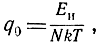
где Еи - энергия импульса на входе приемника.
Тогда пороговая энергия импульса будет равна
Епор = qпорNkT. (5.60)
При неоптимальной фильтрации высокочастотного импульса q < q0 (рис. 5.2), вследствие чего пороговая энергия импульса будет в q0/q раз больше, т. е.
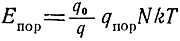
или
Eпор = mNkT, (5.61)
где
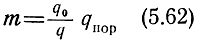
- коэффициент пропорциональности, который условимся называть коэффициентом наблюдаемости.
Определив пороговую энергию импульса, можно, при известной форме импульса, найти пороговую мощность.
Действительно, энергия импульса на входе приемника равна
Еи = Риτэфф,
где Ри - импульсная мощность входного сигнала;
τэфф - эффективная длительность импульса, равная
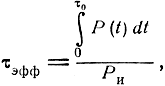
где Р(t) - форма импульса по мощности;
τ0 - длительность импульса по основанию.
Тогда пороговая мощность
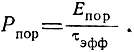
Подставив значение Епор из формулы (5.61), получим
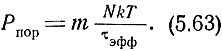
При прямоугольной форме импульса τэфф = τ. Поэтому
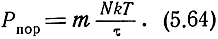
Так как между Pпор и qпор существует линейная зависимость, что следует из формул (5.62) и (5.63), то характер зависимости Рпор от n будет таким же, как и характер зависимости qпор от n (рис. 5.16). В частности, при малых значениях n (n < 10) Рпор будет пропорциональна 1/n, а при больших значениях n (n > 100) Рпор будет пропорциональна 1/√n.
Что касается числа интегрируемых импульсов, то оно определяется режимом работы радиолокатора и свойствами интегратора. Так, в случае, когда радиолокатор работает в режиме слежения за целью, а интегратор не обладает насыщением
n = FиTнаб,
где Fи - частота повторения импульсов,
Тнаб - время наблюдения.
Как видим, при неограниченном возрастании Тнаб будет неограниченно возрастать и n, вследствие чего Рпор будет неограниченно уменьшаться.
Если радиолокатор работает в режиме кругового или секторного обзора, а время эффективного интегрирования не превышает периода обзора (интегратор обладает насыщением)
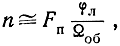
где φл - ширина луча на уровне 0,5 по мощности;
Ωоб - угловая скорость обзора.
Определим теперь пороговую энергию импульса и пороговую мощность при оптимальной фильтрации пачки высокочастотных импульсов. В этом случае отношение сигнал/шум согласно формуле (5.11) равно
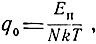
где Еи - общая энергия пачки импульсов.
При прямоугольной форме огибающей пачки импульсов
Еи = nЕи.
Следовательно,
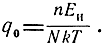
Поэтому пороговая энергия импульса
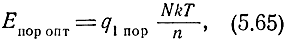
а пороговая мощность
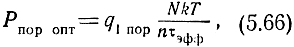
При прямоугольной форме импульса
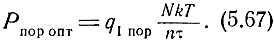
Здесь q1 пор - пороговое значение сигнал/шум при n = 1.
Полученные формулы позволяют сравнить эффективность оптимальной фильтрации пачки импульсов с эффективностью последетекторного интегрирования.
Выше указывалось, что в случае, когда полоса пропускания приемника согласована с длительностью импульса, условия фильтрации одиночного высокочастотного импульса весьма близки к оптимальным, вследствие чего q ≅ q0 (рис. 5.2).
Тогда согласно формулам (5.62) и (5.63)
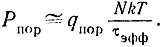
Из рис. 5.16 видно, что при малом числе интегрируемых импульсов (n < 10)
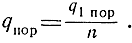
Следовательно,
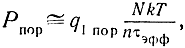
что совпадает с формулой (5.66).
Как видим, в случае малого числа импульсов в пачке (n < 10) пороговая мощность при оптимальной фильтрации одиночного импульса с последующим последетекторным интегрированием импульсов пачки будет примерно такой же, как и при оптимальной фильтрации пачки импульсов.
Однако при n > 10, как видно из рис. 5.16,
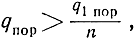
вследствие чего пороговая мощность при последетекторном интегрировании импульсов пачки будет больше, чем при оптимальной фильтрации пачки импульсов. Это различие в значениях пороговых мощностей будет тем больше, чем больше число импульсов в пачке.
Таким образом, оптимальная фильтрация одиночного импульса совместно с последетекторным интегрированием импульсов пачки при n > 10 является менее эффективным средством уменьшения пороговой мощности, чем оптимальная фильтрация пачки импульсов.
Однако не следует упускать из виду, что оптимальная фильтрация пачки импульсов возможна только при когерентности импульсов в пачке и требует применения довольно сложных гребенчатых фильтров, в то время как обеспечение последетекторного интегрирования импульсов пачки не вызывает каких-либо серьезных затруднений.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
