Глава седьмая. Факторы, определяющие точность определения местоположения цели

7.1. Ошибки линий положения

Выше неоднократно указывалось, что при измерении какой-либо геометрической величины, характеризующей местоположение цели, возникают систематические и случайные ошибки. Величины этих ошибок зависят от правильности учета реальных условий распространения радиоволн, величины отношения сигнал/помеха и, наконец, степени технического совершенства радиолокатора. Систематические ошибки в принципе могут быть устранены. Случайные ошибки, наоборот, устранены быть не могут. Поэтому измеренная геометрическая величина будет в общем случае отличаться от истинной, вследствие чего найденная линия положения не будет совпадать с истинной.

Расстояние между истинной и найденной линиями положения называется ошибкой линии положения.

Для определения зависимости ошибки линии положения от ошибки геометрической величины воспользуемся теорией скалярного поля.

Семейство линий положения можно рассматривать как линии уровня плоского скалярного поля геометрической величины U.

Из теории поля известно, что

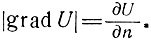
Заменяя дифференциалы конечными приращениями, получаем ошибку линии положения, равную

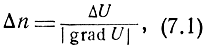
где ΔU - ошибка геометрической величины.

Из формулы (7.1) следует, что ошибка линии положения прямо пропорциональна ошибке геометрической величины. Поэтому закон распределения ошибок линий положений будет таким же, как и ошибок геометрической величины. Ранее указывалось, что в подавляющем большинстве случаев закон распределения ошибок геометрической величины достаточно точно описывается нормальным законом распределения, который вполне характеризуется средней квадратической ошибкой.

Поэтому точность определения линии положения также вполне характеризуется средней квадратической ошибкой линии положения. Коэффициент пропорциональности между средней квадратической ошибкой линии положения и средней квадратической ошибкой геометрической величины зависит от вида линии положения и взаимного расположения искомой точки и фиксированных.

Линия положения постоянного пеленга (рис. 1.5 и 1.6) в декартовой системе координат описывается следующим уравнением:

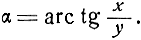
Модуль градиента в той же системе координат равен

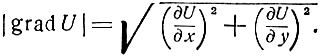
Поэтому в рассматриваемом случае

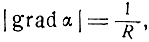
где R - расстояние между искомой точкой и фиксированной.

Тогда согласно формуле (7.1) ошибка линии положения при пеленгации будет равна

где Δα - ошибка пеленга в радианах.

Заменяя Δα средней квадратической ошибкой пеленга за найдем среднюю квадратическую ошибку линии положения при пеленгации как

Линия положения постоянного расстояния (рис. 1.8) описывается уравнением

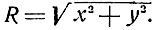
Поэтому

Тогда ошибка линии положения при дальнометрии будет равна

где ΔR - дальномерная ошибка.

Соответственно, средняя квадратическая ошибка линии положения при дальнометрии будет равна

где σ_R - средняя квадратическая ошибка дальности.

Гиперболическая линия положения (рис. 1.9) описывается уравнением

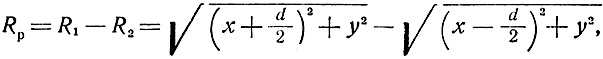
где d - база разностно-дальномерной системы.

Поэтому

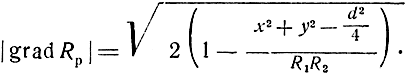
Из ΔАМВ следует, что

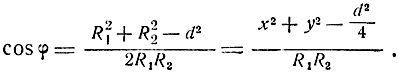
Поэтому

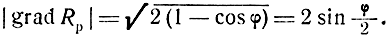
Тогда ошибка гиперболической линии положения будет равна

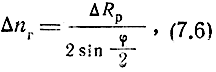
Где ΔR_р - ошибка разности расстоянии,

φ - угол между фокальными радиусами-векторами.

Заменяя ΔR_р средней квадратической ошибкой разности расстояний σ_p, найдем среднюю квадратическую ошибку гиперболической линии положения как

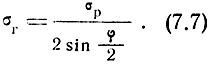
Если расстояние R от середины базы до точки М (рис. 1.9) значительно больше базы d, то

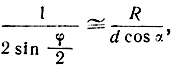
где α - угол между нормалью к середине базы и радиусом-вектором R.

Тогда

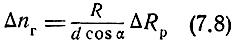
и

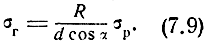
Эллиптическая линия положения (рис. 1.10) описывается уравнением

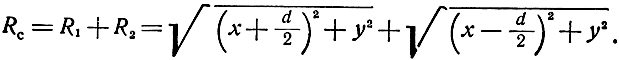
Поэтому

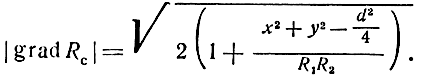
Из ΔАМВ следует, что

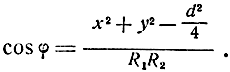
Поэтому

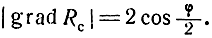
Тогда ошибка эллиптической линии положения будет равна

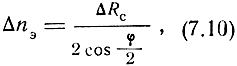
где ΔR_c - ошибка суммы расстояний,

φ - угол между фокальными радиусами-векторами.

Заменяя ΔR_c средней квадратической ошибкой суммы расстояний σ_с, получим среднюю квадратическую ошибку эллиптической линии положения как

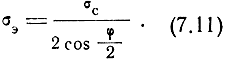
Полученные формулы позволяют сделать следующие выводы.

При пеленгации ошибка линии положения, как это следует из формулы (7.2), при неизменной ошибке пеленга увеличивается с увеличением расстояния до объекта.

При дальнометрии ошибка линии положения согласно формуле (7.4) равна дальномерной ошибке и, следовательно, зависит от расстояния так же, как и дальномерная ошибка.

При измерении разности расстояний ошибка линии положения, как это следует из формулы (7.6), уменьшается с возрастанием расстояния между фиксированными точками. Следовательно, для повышения точности определения линии положения необходимо указанное расстояние увеличивать.

При измерении суммы расстояний, наоборот, целесообразно уменьшать расстояние между фиксированными точками, так как наименьшая ошибка линии положения, как это следует из формулы (7.10), будет при φ = 0, т. е. при d = 0.

Существенно отметить, что при одинаковых ошибках измерения интервалов времени наибольшую точность определения линии положения обеспечивает дальномерная система. Точность эллиптической системы будет в 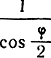раз хуже. Точность гиперболических систем так же будет хуже в 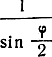раз.

Существенно также, что коэффициент пропорциональности между ошибкой линии положения и ошибкой измеряемой геометрической величины для азимутальных и дальномерных систем, как это следует из формул (7.2) и (7.4), не зависит от направления. Поэтому азимутальные и дальномерные системы являются всенаправленными.

Для гиперболических и эллиптических систем указанный коэффициент, как это следует из формул (7.6) и (7.10), зависит от направления. Поэтому гиперболические и эллиптические системы не являются всенаправленными. Так, для гиперболической системы коэффициент пропорциональности между ошибкой линии положения и ошибкой разности расстояний согласно формуле (7.6) будет

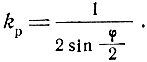
Следовательно, для случая, когда средняя квадратическая ошибка разности расстояний не зависит от положения искомой точки относительно фиксированных, линии постоянных значений средних квадратических ошибок линий положения будут представлять собой окружности, опирающиеся на базу. Наибольшая точность определения гиперболической линии положения будет на направлении, совпадающем с нормалью к середине базы, а наименьшая - на направлении, совпадающем с базой.