7.2. Точность определения местоположения

Рассмотрим сначала случай определения местоположения объекта на плоскости.

Пусть, например, местоположение цели определяется пеленгационным методом (рис. 7.1). Если при измерении пеленгов точки М возникли ошибки Δα₁ и Δα₂, то найденное место точки М будет отличаться от истинного на величину ММ₀.

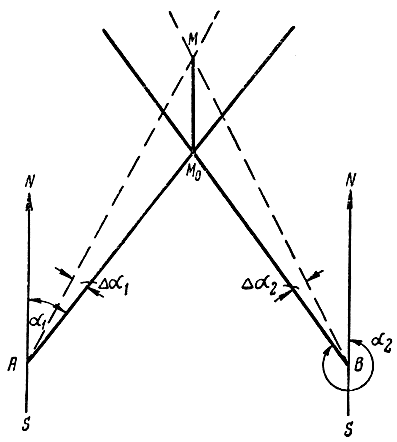
Рис. 7.1. Ошибка места, возникающая при определении местоположения пеленгационным методом

Расстояние между истинным местоположением и найденным называется ошибкой места. Очевидно, что при известных величинах ошибок Δα₁ и Δα₂ определение ошибки места ММ₀ не вызывает затруднений. Однако, как уже указывалось ранее, величины случайных ошибок, возникающих при измерении пеленгов, так же как и при измерении любых других величин, неизвестны. Встает в связи с этим вопрос, как характеризовать точность местоопределения?

Пусть линий положений пересекаются под углом γ (рис. 7.2), а их случайные ошибки U и V подчиняются нормальным законам распределения.

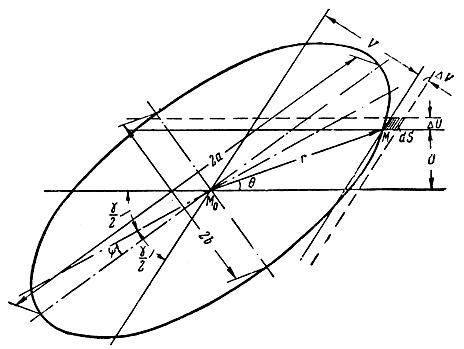
Рис. 7.2. Кривая равной плотности распределения вероятностей ошибок. (Эллипс ошибок)

Из теории вероятностей известно, что двумерная плотность распределения вероятностей ошибок U и V в этом случае будет

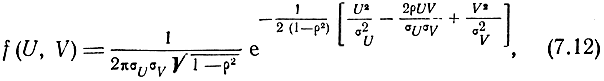
где σ_U и σ_V - средние квадратические ошибки линий положения,

ρ - коэффициент корреляции.

Коэффициент корреляции характеризует степень вероятностной связи между случайными ошибками U и V и равен

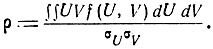
Если случайные ошибки U и V независимы, то ρ = 0. Приравнивая показатель степени при е в формуле (7.12) некоторой постоянной величине, получим уравнение кривой равной плотности распределения вероятностей

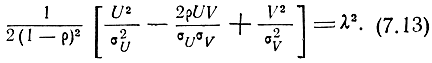
Можно показать, что кривая равной плотности распределения представляет собой эллипс (рис. 7.2).

Различным значениям параметра λ соответствует семейство софокусных эллипсов, которые принято называть эллипсами ошибок.

Вероятность нахождения искомого местоположения в пределах эллипса с параметром λ будет равна

откуда

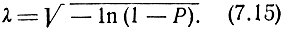
Так, для эллипса ошибок, обладающего тем свойством, что вероятность нахождения в нем искомого местоположения равна 1/2, значение параметра λ = 0,832.

Размеры полуосей эллипса ошибок при ρ = 0 будут равны

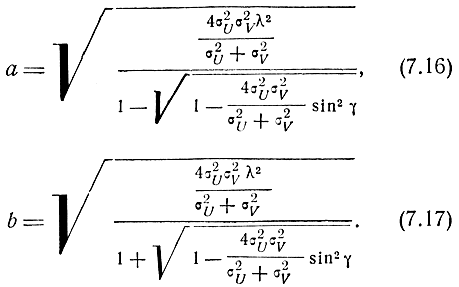
Угол ψ, определяющий положение эллипса ошибок (рис. 7.2), будет равен

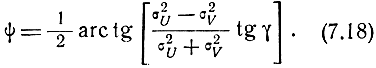
Анализ возможных положений эллипса ошибок при различных значениях σ_U, σ_V и γ позволяет сделать следующий вывод: большая ось эллипса всегда лежит в остром угле пересечения линий положения и ближе к той из них, точность определения которой выше. Иными словами, большая ось эллипса ошибок всегда лежит между биссектрисой острого угла пересечения линий положений и той из линий положения, точность определения которой выше.

В частном случае при одинаковой точности определения линий положения большая ось эллипса совпадает с биссектрисой острого угла пересечения линий положения.

В другом частном случае, когда угол пересечения прямой, оси эллипса ошибок совпадают с линиями положения.

Если при этом σ_x = σ_y, то эллипсы ошибок превращаются в окружности, и эллиптическое рассеивание превращается в круговое.

Итак, точность определения местоположения объекта на плоскости наиболее полно характеризуется эллипсом ошибок.

Поэтому наиболее полное представление о зависимости точности местоопределения от взаимного расположения искомой точки и фиксированных дает так называемое поле ошибок, представляющее собой ряд эллипсов ошибок заданной вероятности.

Приведенные выше формулы позволяют построить поле ошибок и заданных конкретных условиях; при этом необходимо иметь опытные данные о зависимости средних квадратических ошибок геометрических величин от взаимного расположения искомой точки и фиксированных.

Если по каким-либо причинам эти зависимости неизвестны, то в первом приближении для ориентировочного суждения о поле ошибок можно принять средние квадратические ошибки геометрических величин постоянными.

Для иллюстрации на рис. 7.3 представлено поле ошибок при дальномерно-пеленгационном методе местоопределения.

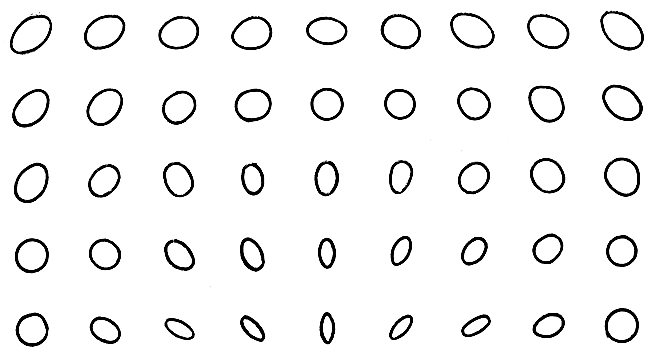
Рис. 7.3. Поле ошибок при дальномерно-пеленгационном методе местоопределения

Рассмотрим теперь случай определения местоположения объекта в пространстве дальномерно-пеленгационным методом. Если при измерении дальности R, азимута а и угла места β возникли ошибки ΔR, Δα и Δβ, то найденное местоположение цели не будет совпадать с истинным. Ошибка места r в этом случае будет равна расстоянию М₀М (рис. 7.4). Составляющие ошибки Места по трем взаимно перпендикулярным осям X, Y и Z будут равны

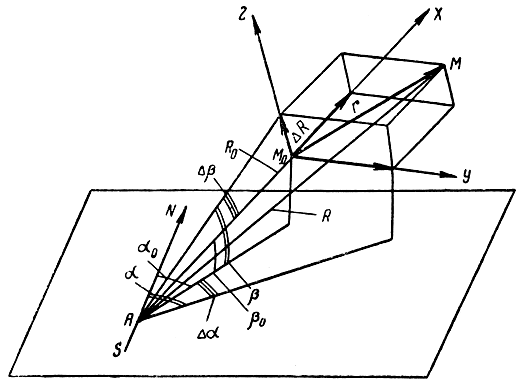
Рис. 7.4. Ошибка места при дальномерно-пеленгационном методе определения местоположения

Если случайные ошибки x, y и z взаимно Независимы и подчиняются нормальным законам распределения, что в радиолокации обычно выполняется, то трехмерная плотность распределения вероятностей будет равна

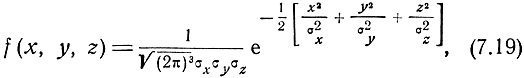
где

а σ_R, σ_α, σ_β - средние квадратические ошибки по дальности, азимуту и углу места.

Приравнивая показатель степени е в формуле (7.19) некоторой постоянной величине, получаем уравнение поверхности равной плотности распределения вероятностей

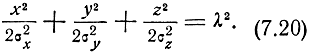
Эта поверхность представляет собой эллипсоид с центром в начале координат и осями, совпадающими с осями координат. Различным значениям λ соответствует семейство софокусных эллипсоидов, которые условимся называть эллипсоидами ошибок.

Можно показать, что вероятность нахождения искомого местоположения в пределах эллипсоида ошибок будет равна

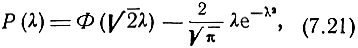
где Ф(√2λ) - интеграл вероятности.

Для эллипсоида ошибок, обладающего тем свойством, что вероятность нахождения в нем искомого местоположения равна 0,5, значение параметра λ = 1,088.

Полуоси эллипсоида ошибок будут равны

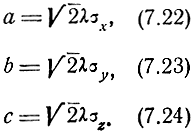
Если σ_x = σ_y = σ_z, то эллипсоид ошибок превращается в сферу ошибок и эллипсоидное рассеивание превращается в сферическое.