7.3. Ошибки места

В предшествующем параграфе было показано, что наиболее полное представление о точности местоопределения на плоскости дает эллипс ошибок, а в пространстве - эллипсоид ошибок. Вместе с тем остался открытым вопрос о вероятности появления ошибки места в заданных пределах. Для ответа на поставленный вопрос необходимо найти функцию распределения вероятностей ошибки места, под которой понимают вероятность того, что ошибка места не будет превосходить значения наперед заданной величины r.

Другими словами, функция распределения ошибок места определяет вероятность нахождения найденного местоположения в пределах окружности с радиусом, равным r.

Прежде всего найдем среднюю квадратическую ошибку места.

Из рис. 7.2 следует, что

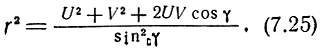
В теории вероятностей доказывается, что среднее значение суммы случайных величин равно сумме средних значений слагаемых. Поэтому

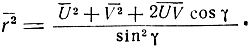
Так как при нормальном законе распределения

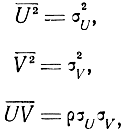
то

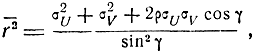
откуда средняя квадратическая ошибка места равна

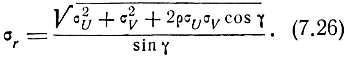
При ρ = 0

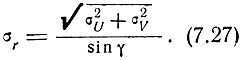
Найдем теперь плотность распределения вероятностей ошибок места. С этой целью выполним преобразование переменных выражения (7.12) по следующей формуле:

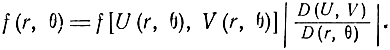
Так как

а модуль якобиана равен

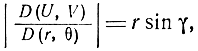
то

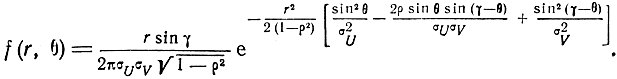
Откуда плотность распределения вероятностей ошибок места равна

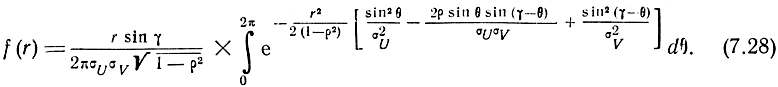
Соответственно функция распределения вероятностей ошибок места будет равна

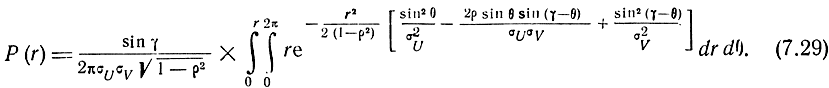
В частном случае, когда γ = π/2, ρ = 0, σ_U = σ_V = σ, т. е. при круговом рассеивании

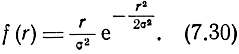
Как видим, в этом случае плотность распределения вероятностей ошибок места описывается законом Релея.

Существенно, что релеевское распределение значительно отличается от нормального. Если при нормальном законе распределения наивероятнейшее значение случайной величины имеет место при r = 0, то при релеевском законе максимальная плотность распределения вероятностей - при r = σ. Следовательно, при релеевском законе распределения ошибок места наивероятнейшее ее значение равно средней квадратической ошибке линии положения.

Кроме того, при релеевском распределении ошибок места в отличие от нормального распределения средняя квадратическая ошибка места не равна корню квадратному из дисперсии.

Функция распределения ошибок места при круговом рассеивании равна

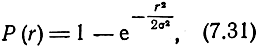
откуда радиус окружности ошибок заданной вероятности будет равен

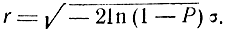
Поскольку в рассматриваемом случае средняя квадратическая ошибка места согласно формуле (7.27) равна

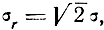
то

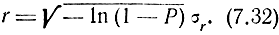
График функции распределения по релеевскому закону представлен на рис. 7.5 (график при m = 1).

В другом, более общем случае, когда 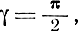ρ = 0, но σ_U = σ_x ≠ σ_V = σ_y, т. е. при таком эллиптическом рассеивании, когда оси эллипса ошибок совпадают с линиями положения

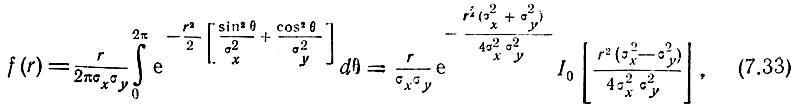
где I₀ - модифицированная функция Бесселя нулевого порядка.

Функция распределения ошибок места в рассматриваемом случае будет равна

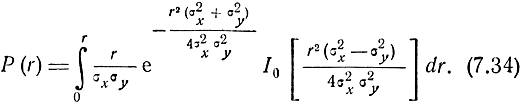
На рис. 7.5 представлены графики функции распределения вероятностей ошибок места в зависимости от отношения 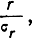соответствующие различным значениям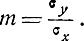

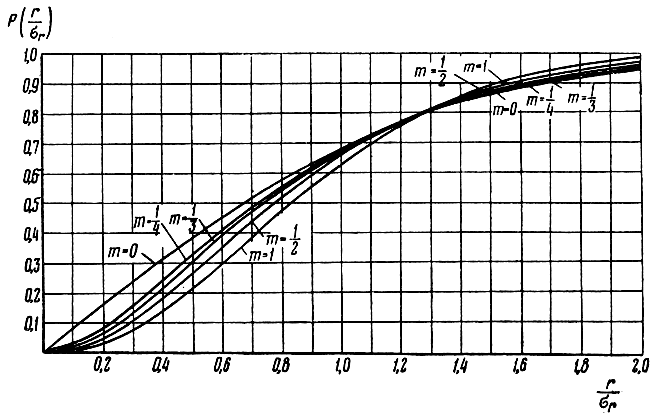
Рис. 7.5. Графики функции распределения вероятности по закону Релея

Между прочим, приведенные графики верны и для общего случая, когда 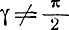и ρ ≠ 0. Только в этом случае под m следует понимать отношения малой полуоси эллипса ошибок к большой.

Как видим, функции распределения ошибок места как при круговом рассеивании (m = 1), так и при эллиптическом (0 < m < 1) отличаются от функции распределения нормального закона (m = 0). Однако при P(r) > 0,6 эти различия не столь велики. Так, вероятность того, что ошибка места не будет превосходить величины σ_r и 2σ_r лежит соответственно в пределах 0,63-0,68 и 0,95-0,98.

Таким образом, точность местоопределения на плоскости можно характеризовать либо эллипсом ошибок заданной вероятности, либо величиной средней квадратической ошибки места.

Рассмотрим теперь ошибки места в пространстве.

Из рис. 7.4 видно, что

Поэтому среднее значение квадрата ошибки места будет равно

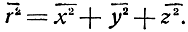
Так как при нормальном законе распределения

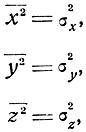
то

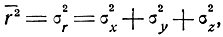
откуда средняя квадратическая ошибка места равна

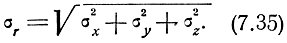
Что же касается функции распределения ошибок места в пространстве, то ограничимся рассмотрением только случая сферического рассеивания.

Так как при сферическом рассеивании σ_х = σ_y = σ_z = σ, то согласно формуле (7.22) радиус сферы будет равен

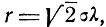
откуда

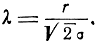
Подставляя это значение λ в формулу (7.21), получаем

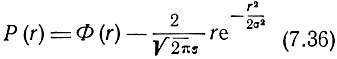
Плотность распределения вероятностей ошибок места при сферическом рассеивании равна

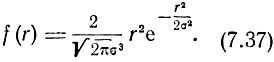
Как видим, при сферическом рассеивании плотность распределения вероятностей ошибок места описывается законом Максвелла.

График максвелловского закона распределения представлен на рис. 7.6.

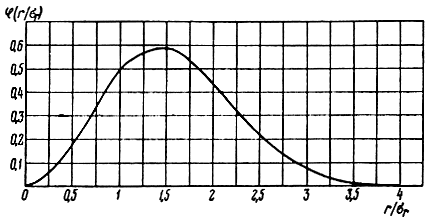
Рис. 7.6. График плотности распределения вероятности по закону Максвелла

Средняя квадратическая ошибка места в этом случае согласно формуле (7.35) равна

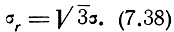
При максвелловском распределении ошибок места в отличие от нормального распределения, средняя квадратическая ошибка места не равна корню квадратному из дисперсии.

График функции распределения ошибок места при сферическом рассеивании представлен на рис. 7.7. Кроме того, на том же рисунке представлен график функции распределения по номинальному закону.

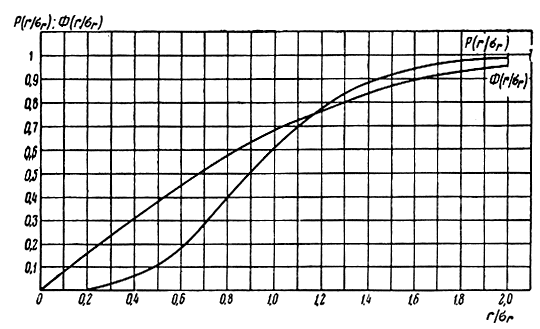
Рис. 7.7. График функции распределения ошибок места при сферическом рассеивании

Как видим, функция распределения ошибок места при сферическом рассеивании отличается от нормального распределения. Однако при Р(r) > 0,6 эти различия незначительны.

Вероятность того, что ошибка места при сферическом рассеивании не будет превосходить величины σ_r и 2σ_r, равна соответственно 0,61 и 0,99.

Что касается функции распределения ошибок места при эллипсовидном рассеивании, то ограничимся замечанием, что графики этих функций не будут выходить за пределы двух графиков, представленных на рис. 7.7.

Итак, точность местоопределения в пространстве можно характеризовать либо эллипсоидом ошибок заданной вероятности, либо величиной средней квадратической ошибки места.