§ 2.5. Учет сферичности земной поверхности при пользовании интерференционными формулами

При расстояниях между передатчиком и приемником 0,2r₀ < r < 0,8r₀ следует учитывать сферичность Земли. Схема распространения радиоволн с учетом сферичности Земли изображена на рис. 2.14.

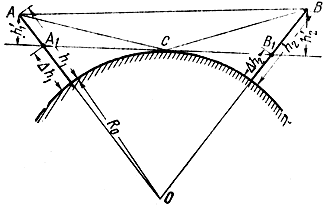
Рис. 2.14. Учет влияния сферичности Земли на распространение радиоволн при r < 0,8r₀

Если в точке отражения волны провести плоскость, касательную к земному шару, и отсчитывать высоты антенн от этой плоскости, то картина распространения радиоволн над сферической Землей будет аналогична картине распространения волн над плоской поверхностью.

Для определения напряженности поля на расстояниях, меньших r₀, можно пользоваться формулой (2.29), подставляя в нее вместо действительных высот антенн h₁ и h₂ приведенные высоты h₁′ и h₂′.

При таком подходе разность хода лучей сохраняется и угол падения волны на поверхность Земли остается неизменным, следовательно, результат будет правильным.

Для расчета напряженности поля нужно найти приведенные высоты h₁′ и h₂′ по известным высотам h₁ и h₂ и расстоянию r. Если бы рис. 2.14 был изображен с соблюдением масштаба, то было бы видно, что высоты h₁ и h₁′ почти не имеют углового расхождения и можно считать

Из треугольников ОА₁С и ОСВ₁ можно найти

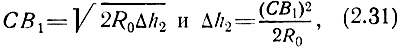
где R₀ - радиус земного шара.

Определение положения точки отражения С в общем случае связано с громоздкими вычислениями. Рассмотрение крайних случаев малых и больших расстояний можно упростить.

При небольших расстояниях положение точки отражения можно найти так же, как для плоской земной поверхности:

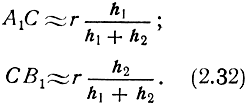
При значительных расстояниях, близких к расстоянию прямой видимости, прямая А₁В₁ и ломаная АСВ почти сливаются, и можно считать

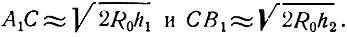
Учитывая, что

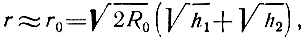
находим

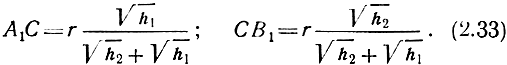
Для промежуточных случаев положение точки С берут как среднее из двух положений, определяемых формулами (2.32) и (2.33).