§ 4.9. Преломление и отражение радиоволн в ионосфере

Электронная плотность ионосферы сначала возрастает с высотой над земной поверхностью, на высоте 300÷400 км имеет максимум, а затем убывает, как это схематически показано на рис. 4.10, а. Следовательно, диэлектрическая проницаемость ионосферы убывает с высотой, имеет минимум на высоте максимума электронной плотности и возрастает до единицы при дальнейшем увеличении расстояния от Земли (рис. 4.10, б). В неоднородной среде траектория волны искривляется, что может привести к отражению радиоволн.

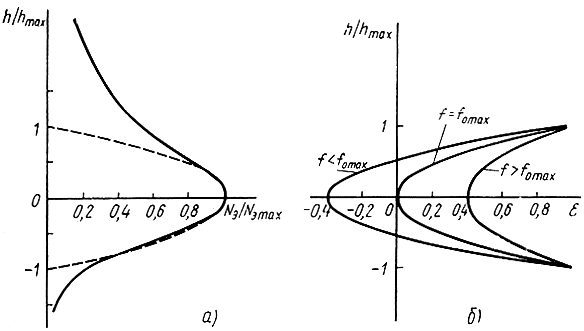
Рис. 4.10. Изменение параметров ионосферы с высотой: а - электронная плотность; простой слой; аппроксимация параболическим законом; б - диэлектрическая проницаемость для трех рабочих частот

Рассмотрим траекторию распространения волны в неоднородной ионосфере, свойства которой меняются с высотой, а в горизонтальном направлении остаются постоянными. Для простоты будем считать земную поверхность и ионосферу плоскими.

Разобьем ионосферу на тонкие слои, в пределах каждого из которых диэлектрическую проницаемость будем считать постоянной (рис. 4.11, а). Тогда уравнение движения волны запишется так же, как для случая распространения радиоволны в слоистой тропосфере [см. уравнение (3.22)].

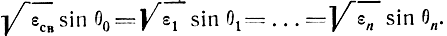
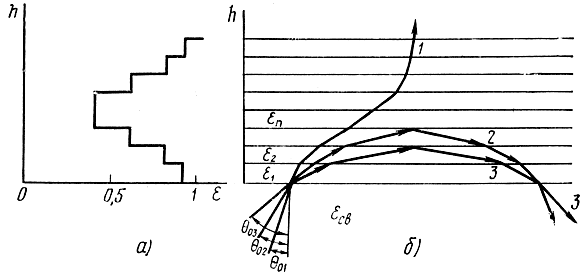
Рис. 4.11. Отражение радиоволн от плоской слоистой ионосферы: а - схема ступенчатого изменения ε ионосферы с высотой; б - отражение радиоволн от ионосферы при различных углах падения θ₀₁ < θ₀₂ < θ₀₃

При уменьшении толщины слоев, т. е. при плавном изменении ε траектория волны в пределе обратится в кривую. При убывании ε с высотой на каждый последующий слой волна будет падать под все большим углом, так что на некоторой высоте могут создаться условия для полного внутреннего отражения и волна пойдет параллельно границе раздела слоев. При небольшой неоднородности ионосферы направление волны может отклониться вниз и тогда волна, преломляясь, вернется на Землю, т. е. произойдет отражение волны (рис. 4.11, б).

Таким образом, в ионосфере отражение радиоволн происходит не на границе воздух - ионизированный газ, а в толще ионизированного газа. Отражение может произойти только в той области ионосферы, где диэлектрическая проницаемость убывает с высотой, а следовательно, электронная плотность возрастаете высотой, т. е. ниже максимума электронной плотности ионосферного слоя.

Выясним соотношение между электронной плотностью, углом падения волны на нижнюю границу ионосферы и рабочей частотой, которое должно быть выполнено, для того чтобы произошли отражения радиоволн от ионосферы. Угол полного внутреннего отражения согласно выражению (1.73) при плавном изменении диэлектрической проницаемости с высотой близок к 90°, поскольку sin θ_кр ≈ 1.

На нижней границе ионосферы величину ε_св можно принять равной единице. Тогда из уравнения траектории волны (3.22) можно записать условие отражения:

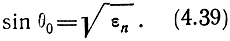
Условие отражения связывает угол падения волны на нижнюю границу ионосферы с диэлектрической проницаемостью в толще самой ионосферы, на той высоте, где происходит отражение волн.

Перепишем условие отражения, подставив в него выражение (4.6) для диэлектрической проницаемости ионизированного газа (потери энергии не учитываются)

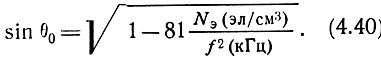
Следовательно, при определенной электронной плотности волна данной частоты отразится только в том случае, если угол падения θ₀ равен или превышает величину, определяемую (4.40). Чем больше электронная плотность N_э, тем при меньших значениях угла 60 возможно отражение. Угол θ_0кр, при котором в данных условиях еще возможно отражение, называют критическим углом (рис. 4.12).

Из выражения (4.40) можно определить максимальную рабочую частоту волны, которая отразится от ионосферы при заданных величинах электронной плотности и угла падения волны на слой:

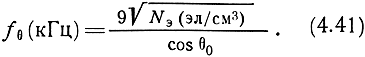
Чем больше угол падения волны на ионосферу, тем большая электронная плотность требуется для отражения и тем на большей высоте происходит отражение (см. рис. 4.11, б).

Если волна падает нормально на слой ионосферы, то с учетом (4.7)

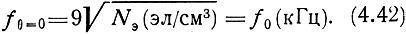
При нормальном падении волны отражение происходит на той высоте, где рабочая частота равна собственной частоте плазмы и, следовательно, ε = 0. Из (4.41) и (4.42) видно, что для отражения волн, посланных нормально и под углом 6 к ионосфере, нужна одна и та же электронная плотность, если f₀ = f₀/cosθ₀. Отражение этих волн происходит на одной и той же высоте.

В случае одной и той же электронной плотности ионосферы при наклонном падении может отразиться волна, частота которой в sec θ₀ раз превышает частоту волны, отражающейся при вертикальном падении на слой:

Это соотношение называется законом секанса.

Чем больше электронная плотность, тем для более высоких частот выполняется условие отражения.

Максимальная частота, при которой волна отражается в случае вертикального падения на ионосферный слой, называется критической частотой f_кр (отражение происходит вблизи максимума ионизации):

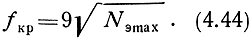
Если рабочая частота больше критической, то при нормальном падении волны на ионосферу отражения не происходит и волна уходит в космическое пространство. Коэффициент отражения равен нулю.

Таким образом, коэффициент отражения волны от ионосферы меняется в зависимости от частоты скачком при f = f_кр. Если рабочая частота меньше критической, то происходит полное отражение волны от ионосферного слоя. Коэффициент отражения равен единице. При наклонном падении волны ионосфера прозрачна для частот, превышающих максимальную частоту [см. уравнение (4.41)].

При распространении радиоволн на большие расстояния условия отражения необходимо рассматривать с учетом сферичности Земли и ионосферы. Уравнение траектории волны в сферически слоистой среде описывается уравнением (3.19), которое применительно к ионосфере (см. рис. 4.12) можно переписать в виде

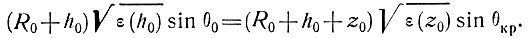
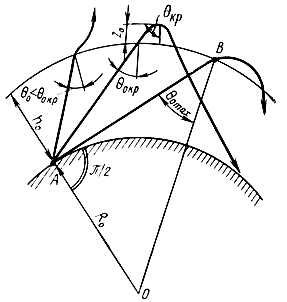
Рис. 4.12. Условие отражения радиоволн от ионосферы с учетом сферичности Земли и ионосферы

Полагая √ε(h₀) = 1 и учитывая, что при отражении sin θ_кр = 1, получаем условие отражения:

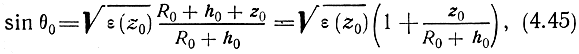
где z₀ - высота точки отражения над нижней границей ионосферного слоя.

Подставляя в (4.45) выражение для ε (4.8) и решая относительно частоты, получаем соотношение между частотами радиоволн, отражающихся в случае вертикального и наклонного падения на ионосферу при одной и той же электронной плоскости:

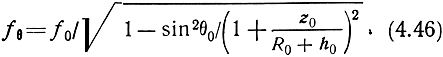
Максимальная частота волны, отражающейся при наклонном падении на ионосферу,

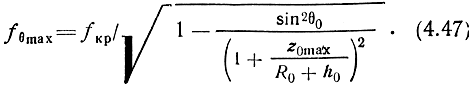
Частота f_0max зависит от критической частоты, высоты отражающего слоя и угла падения волны на ионосферу.

Формулу (4.46) приводим к виду, аналогичному (4.43):

где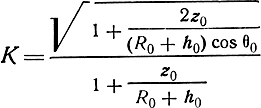  

- поправочный коэффициент, учитывающий сферичность Земли и ионосферы.

Сферичность Земли и ионосферы ограничивает максимальный угол падения волны на ионосферу.

Из рис. 4.12 видно, что волна, направленная по касательной к Земле, падает на ионосферу под наибольшим возможным при данной высоте слоя углом θ_0max. Из треугольника АОВ имеем

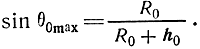
То обстоятельство, что волна не может быть послана под углом, большим θ_0max, приводит к ограничению рабочего диапазона.

При заданной электронной плотности N_{э max} может отразиться волна, частота которой не превышает

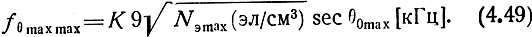
Так, если отражение происходит на высоте 200 км, то отношение

Практически от ионосферы могут отражаться волны длиннее 10 м.