§ 4.10. Применимость приближения геометрической оптики при исследовании отражения радиоволн от ионосферы

Распространение и отражение радиоволн в ионосфере мы рассматривали с позиций геометрической оптики.

Выясним справедливость такого подхода для случая нормального падения волны на слой ионосферы. Как и раньше, будем считать ионосферу плоскослоистой средой, т. е. предположим, что диэлектрическая проницаемость меняется только в вертикальном направлении вдоль оси h (см. рис. 4.10).

В этом случае напряженность поля Е зависит только от координаты h и должна удовлетворять волновому уравнению

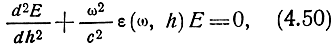
где ε - функция частоты и высоты.

Если бы ионосфера была однородной, то решение уравнения (4.50) записалось бы в виде

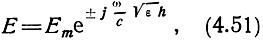
Если среда неоднородна, но на протяжении длины волны ее свойства меняются мало, то распространение волн на небольшом участке пути близко к распространению волн в однородной среде с коэффициентом преломления, соответствующим данному участку неоднородной среды. Таким образом, распространение радиоволн в неоднородной среде должно быть примерно таким же, как распространение радиоволн в однородной среде с меняющейся диэлектрической проницаемостью. Это значит, что уравнение в этом случае должно быть аналогичным (4.51) с заменой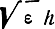  

на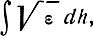  

т. е. иметь вид

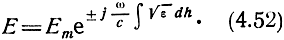
Условие медленного изменения свойств среды на протяжении длины волны считается выполненным, если соблюдается неравенство

где λ_ср - длина волны в среде.

На протяжении длины волны в среде отклонение диэлектрической проницаемости от среднего значения должно быть значительно меньше этой величины.

Условие применимости приближения геометрической оптики не соблюдается, если имеется резкое изменение диэлектрической проницаемости (велика производная dε/dh) или мала величина диэлектрической проницаемости ε. В ионосфере резкие градиенты ε наблюдаются только при появлении спорадических слоев (см. § 4.3).

Как было показано [см. уравнение (4.42)], отражение радиоволн при нормальном падении на ионосферу происходит в области, где ε → 0. Ясно, что при этом длина волны в среде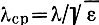  
становится очень большой, и изменение свойств среды на протяжении длины волны не может быть медленным.

Чтобы выяснить, какие явления происходят в случае отражения радиоволн и какова ошибка, возникающая при исследовании процессов отражения с позиций геометрической оптики, рассмотрим результаты строгого решения этой задачи [9].

Распределение электронной плотности по высоте в каждом отдельном слое ионосферы хорошо аппроксимируется параболическим законом:

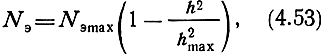
где N_эmax - электронная плотность в максимуме ионосферного слоя; h_max - полутолщина слоя.

Отсчет высоты ведут от максимума слоя (см. рис. 4.10).

Диэлектрическая проницаемость ионосферного слоя меняется согласно выражению (4.8):

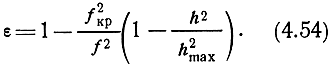
Отражения в точках h = ± h_max не рассматриваются, потому что в действительности имеется плавный переход к области ε = 1 и больших градиентов ε нет.

Подставляя выражение (4.54) в уравнение (4.50), имеем

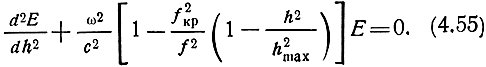
Производя замену переменных, это уравнение можно привести к виду, решаемому в функциях параболического цилиндра.

В решении можно выделить выражение для падающей и отраженной волн и найти соотношение, определяющее коэффициент отражения от ионизированного слоя:

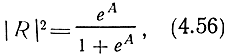
где

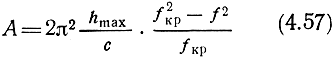
При малых значениях разности. (f²_кр - f²)

Анализ формулы (4.56) показывает, что при f = f_кр |R| = 0,71 - происходит частичное отражение волны; при f >> f_кр |R| → 0 - отражение волны отсутствует; при f << f_кр |R| → 1 - происходит полное отражение волны.

Таким образом, в некотором диапазоне частот часть энергии волны проходит через слой ионосферы и отражение является только частичным. При этом чем больше толщина слоя, тем более резко изменяется коэффициент отражения. На рис. 4.13 представлена частотная зависимость |R| для h_max = 20 и 100 км.

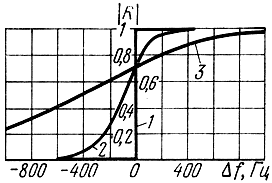
Рис. 4.13. Частотная зависимость коэффициента отражения от ионосферного слоя параболической формы: 1 - геометрическая оптика; 2 - h_m = 100 км; 3 - h_m = 20 км

Для имеющихся в ионосфере толщин регулярных слоев область частичного просачивания волны оказывается очень небольшой. Так, при h_max/λкр = 10 и отклонении частоты Δf/f = ±1,7·10^-2 коэффициент отражения падает и возрастает соответственно до |R|² = 0,001 и |R|² = 0,999.

Таким образом, практически можно считать, что R = 0 при f > f_кр и R =1 при f < f_кр. Критическая частота является предельной частотой волн, отражающихся от слоя ионосферы при нормальном падении волны. Поэтому для целей практики рассмотрение отражения волн от регулярных слоев ионосферы допустимо с позиций геометрической оптики.