Глава 6. Дифференциальный коэффициент шума каскада усилителя с распределенным усилением

6.1. Исходные положения

Усилитель с распределенным усилением является усилительным устройством, в котором реализуется способ уменьшения коэффициента шума, состоящий в построении такой структурной схемы усилителя, чтобы при увеличении числа УЗ, входящих в усилитель, активная мощность шумов от усилительных элементов на его выходе наращивалась медленнее, чем увеличивается коэффициент усиления мощности всего устройства. Этот способ обязан заложенному в каскаде УРУ принципу сложения, благодаря которому избыточный коэффициент шума (F_ш - 1) при некоторых условиях обратно пропорционален числу секций. Данное положительное свойство проявляется, если выполняются совместно следующие условия: расфазировка и потери передающих линий отсутствуют, а также источники шума содержатся только на выходных полюсах эквивалентной схемы УЭ. Однако на практике сочетание данных условий удовлетворяется весьма редко. Поэтому закон изменения составляющих (F_ш - 1) при увеличении n оказывается более сложным.

Шумовые свойства каскада УРУ рассматривались в ряде работ [4, 8, 41]. Полученные в них соотношения для составляющих коэффициента шума носят скорее иллюстративный характер и непригодны для практических расчетов F_ш каскада УРУ на современных УЭ. Наиболее полные сведения о коэффициенте шума приводятся в [8, 41]. Однако и здесь внутренние составляющие, обусловливающие величину F_ш, рассматриваются только для редкого на практике случая, когда источники шума УЭ сосредоточены на их входных или выходных полюсах. Эти источники шума заданы эквивалентами, описываемыми формулой Найквиста через некоторые эквивалентные шумовые сопротивления или проводимости, которые для современных УЭ в литературе не приводятся и непригодны для анализа шумовых свойств многополюсных схем. Полученные .в указанных работах формулы практически не могут быть использованы для инженерного расчета составляющих F_ш в диапазоне частот, с учетом потерь и расфазировки.

В настоящей работе ставится задача вывода формул составляющих дифференциального рабочего коэффициента шума каскада УРУ с различным включением УЭ в передающие линии и их анализа в наиболее важных частных случаях, в которых формулы приводятся к инженерному виду и иллюстрируются расчетными графическими зависимостями. Для получения необходимых соотношений используются рабочие коэффициенты передачи каскада, коэффициенты передачи от источников внутри УЭ, а также принимаются следующие реальные исходные условия: 1) нагрузочные сопротивления чисто активны (Z_i = R_i) и постоянны в диапазоне частот; 2) потери в ПЛ обусловлены только активными составляющими вносимых в фильтры импедансов усилительных элементов; 3) напряжения и токи шумов как функции времени представляют собой случайные стационарные эргодические процессы, подчиняющиеся нормальному закону распределения; 4) известны первоисточники шумов, заданные физическими параметрами и находящиеся либо в цепях нагрузочных сопротивлений, либо в любых ветвях эквивалентной схемы УЭ; 5) источники шума, находящиеся в разных секциях однородного каскада и имеющие одинаковое физическое происхождение, считаются равными; 6) источники шума в разных секциях взаимно статистически независимы.

Введем следующие обозначения: 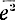- квадраты действующих значений напряжения источников шума; 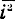- квадраты действующих значений тока источников шума, для одновременного обозначения 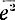и и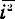спользуем символ ;

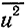Е и J - комплексные амплитуды напряжения и тока источников, для которых физический смысл имеют только их спектральные плотности, для одновременного обозначения Е и J применим символ И; U и I - комплексные амплитуды напряжений и токов в любых участках схемы каскада, для которых физический смысл имеют также только их спектральные плотности [21]^*. Источники шума в каскаде можно подразделить на внутренние и наружные (рис. 6.1). Наружными шумами являются тепловые шумы, возникающие во внутреннем сопротивлении источника сигнала R₁ в балластных сопротивлениях R_2,3 и в сопротивлении нагрузки каскада R₄. Действующее значение напряжения тепловых шумов нагрузочных сопротивлений в бесконечно малой полосе частот определяется формулой Найквиста

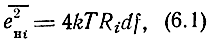
где k = 1,37×10^-23 Вт×с/град - постоянная Больцмана; Т - абсолютная температура, К; R_i (г=1-4)-нагрузочные сопротивления, Ом.

^* (Так же, как в [21], под |E|,|J|, |U|, |I| в случае гармонических сигналов подразумеваем не амплитуды, а среднеквадратические значения.)

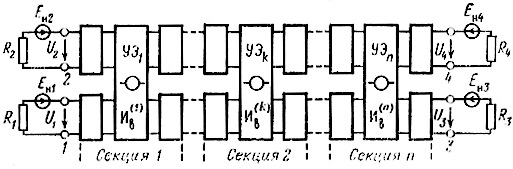
Рис. 6.1. Каскад УРУ с источниками шумов

Внутренние шумы создаются усилительными элементами. Природа внутренних шумов может быть различна (тепловые, дробовые и др.) в зависимости от используемых усилительных элементов (электронных ламп, транзисторов и составных УЭ). Будем анализировать общий случай без конкретизации типа УЭ и природы внутренних шумов. Однако при этом имеем в виду пункт 4 исходных условий. Для "примера приведем выражение для действующего значения внутренних шумов - источника тока дробовых шумов коллекторного перехода транзистора в бесконечно малой полосе частот [42].

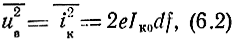
где е - заряд электрона; I_к0 - постоянная составляющая коллекторного тока. В формуле (6.2) фигурируют физические параметры источника шума.

В соответствии с принципом суперпозиции каждый статистически независимый источник шума может рассматриваться в предположении, что остальные источники отсутствуют. Поэтому для каждого такого источника из схемы каскада можно получить четырехполюсник и определить активную мощность на его выходе. Если между какими-либо двумя источниками имеется линейная корреляционная зависимость, то наряду с собственными

активными мощностями может быть определена их взаимная мощность на выходе усилительного устройства. Такими источниками в рассматриваемом случае могут быть источники, находящиеся в одном каком-либо усилительном элементе.

Рассмотрим некоторые функциональные связи между величинами, характеризующими случайный электрический сигнал при прохождении его через линейный четырехполюсник (рис. 6.2). Как известно, полная активная мощность на сопротивлении R_H может быть представлена интегралом от спектральной плотности мощности выходного сигнала.

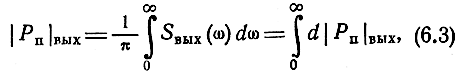
где

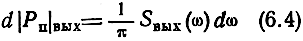
- активная выходная мощность на частоте со в бесконечно малой полосе частот, S_Вых(ω)-спектральная плотность мощности выходного случайного сигнала, которая равна произведению квадрата модуля коэффициента передачи четырехполюсника и спектральной плотности входного источника:

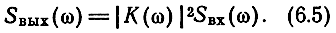
Спектральная плотность входного источника связана с действующим значением напряжения или тока следующим соотношением {43]:

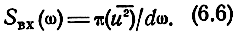
Например, спектральная плотность источника напряжения, описываемого формулой Найквиста (6.1), равна S_c = 2kTR_i и постоянна в диапазоне частот, что является признаком "белого шума". Таким образом, ставя в соответствие некоторым комплексным амплитудам напряжений и токов их действующие значения в бесконечно малой полосе частот

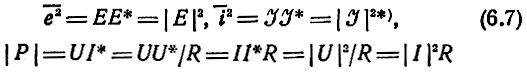
^* ( E^*, U^*, J^*, I^* - величины, комплексно-сопряженные с Е, U, I, I. )

и понимая под преобразованием комплексных амплитуд в результате прохождения шумового сигнала через четырехполюсник преобразование его спектральной плотности, сохраняем весь комплексный аппарат определения напряжений, токов и мощностей через коэффициенты передачи (в том числе и рабочие коэффициенты передачи).

Рис. 6.2. Линейный четырехполюсник