8.3.2. Расчет коэффициента шума

Имея шесть внутренних источников шума УЭ и учитывая внешние шумы балластных сопротивлений R_3,2 и нагрузочного сопротивления R₄, можем представить коэффициент шума каскада в виде суммы следующих составляющих:

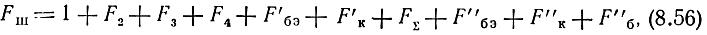
где F_2,3,4 - составляющие наружных шумов, описываемые формулами (6.27), (6.28); F₃ - на нижних частотах равна единице (рис. 6.3); для составляющих используются те же индексы, что и в обозначениях источников шума.

Для оценки составляющих внутренних шумов во всем диапазоне частот необходимо воспользоваться формулой (6.40) с учетом (8.51) - (8.54), (6.32), (6.37) и (5.100). Однако ввиду сложности выражений рассмотрим составляющие внутренних шумов на низких частотах (y → 0). При этом формулы (8.51) - (8.54) упрощаются

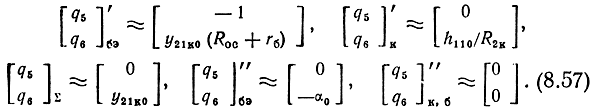
Из (8.57) следует весьма важный вывод о том, что на низких частотах шумы второго транзистора практически не влияют на общий коэффициент шума, так как, во-первых, шумовые коэффициенты коллекторного дробового источника тока и источника тепловых шумов r_б второго транзистора равны нулю и, во-вторых, влиянием i²"_бэ можно пренебречь, поскольку I"_б0 << I'_к0 (8.45), (8.46).

Таким образом, учитывая наиболее существенные составляющие и пользуясь методикой, изложенной в гл. 6, получим

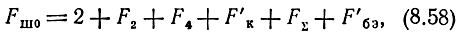
где

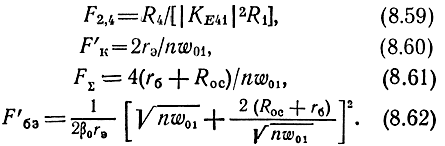
В формулах (8.60), (8.62) использованы соотношения

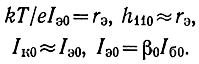
Первое слагаемое в квадратных скобках выражения (8.62), пропорциональное √n, характеризует прохождение шумового сигнала во входную линию и его усиление всеми УЭ. Причем оно оказывается больше второго, благодаря чему F'_бэ становится соизмеримой с F'_к и F_Σ, несмотря на то, что I_б0 << I_к0.

Сумму составляющих F'_к, F_Σ и F'_бэ можно представить в более удобном для анализа виде

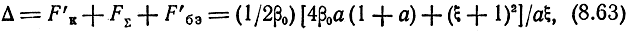
где

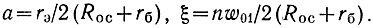
Анализ Δ как основной добавки F_ш0, обусловленной транзисторами, показывает, что увеличение β₀ и уменьшение (R_oc + r_б) приводит к монотонному уменьшению Δ, в то время как в зависимости от r_э, т. е. от I_э0, и nw₀₁ Δ имеет минимум при некоторых оптимальных значениях r_{э opt} и (nw₀₁)_opt. Минимум (в зависимости от r_э вызван ростом F'_к и спадом F'_бэ с увеличением r_э, в зависимости от nw₀₁ обусловлен тем, что наряду с шумами, попадающими в выходную ПЛ и обратно пропорциональными nw₀₁ значительная доля шумов (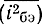) проходит во входную линию, усиливается всеми УЭ и становится, таким образом, пропорциональной nw₀₁.

Проведем анализ минимума Δ. Параллельно анализу будем производить численный расчет величин.

Из уравнения dΔ/da = 0 определяется

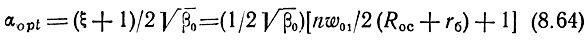
или

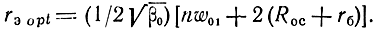
При n = 3, w₀₁ = 76 Ом, β₀ = 50, R_oc = 22 Ом, r_б = 20 Ом, ξ = 2,68 расчет по (8.64) дает a_opt = 0,26, r_эорt = 22 Ом, I_э0 = 1,2 ма (при 7=300 К). Подставляя (8.64) в (8.63), находим

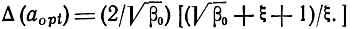
При тех же значениях Δ(a_opt) = 1,14. О том, насколько выражен минимум, можно судить по выражению

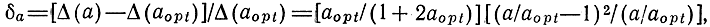
откуда видно, что минимум в зависимости от тока эмиттера выражен чрезвычайно слабо. Действительно, если задать допустимым увеличение Δ(а) по сравнению с Δ(a_opt) на 20% (δ_α = 0,2), то в зависимости от a_opt значения (a/a_opt)_1,2, соответствующие данному δ_a, будут и меть следующие величины:

Проведенный расчет показывает, что в зависимости от тока эмиттера минимум коэффициента шума практически не будет ощущаться. Так, например, даже при a_opt = 1, что является довольно редким случаем, увеличение и уменьшение тока эмиттера в два раза от оптимального дает увеличение Δ всего на 20%. Решение уравнения dΔ/dξ = 0 приводит к выражению

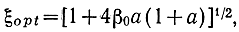
откуда можно определить (nw₀₁)_opt. Тогда

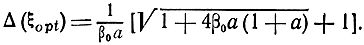
При r_э = 50 Ом, R_oc = 22 Ом, r_б = 20 Ом, β₀ = 50, w₀₁ = 75 Ом имеем значения а =0,06, ξ_opt = 3,7, nw₀₁ = 310 Ом, n = 4, Δ(ξ_opt) = 1,57.

Отклонение ξ от оптимального значения дает приращение

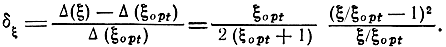
Минимум Δ в зависимости от ξ более ярко выражен по сравнению с предыдущим случаем. Однако и здесь допустимы достаточно широкие пределы отклонения ξ от ξ_opt. Например, для ξ_opt = 3,7, при ξ = 2ξ_opt или ξ =0,5ξ_opt приращение составляет 20%.

Зависимости Δ = f(1/ξ) при a = const проиллюстрированы рис. 8.7, из которого видно, что необходимо стремиться к увеличению а и задавать оптимальное ξ. При этом чем больше а, тем меньше Δ(ξ_opt), а Δ = f(ξ) имеет более пологий характер при отклонении ξ от ξ_opt. Последнее обстоятельство является достаточно важным моментом, поскольку nw₀₁ взятое на основании требований оптимальности АЧХ, как правило, меньше nw₀₁, которое требуется для минимума Δ. Однако при достаточно больших а отличие фактического nw₀₁, выбранного из требований АЧХ, от необходимого nw₀₁ несущественно отразится на величине Δ.

На частотах, где начинают заметно влиять реактивные параметры транзисторов, формулы для составляющих коэффициента шума становятся весьма сложными. Однако на основании численных расчетов и свойств функций, входящих в составляющие F_ш, можно сделать некоторые выводы. По-прежнему подавляющую долю в коэффициент шума вносят источники шумов первого транзистора. При этом F_Σ имеет наибольшую величину. Абсолютное значение F_Σ тем больше, чем больше r_б и R_ос а увеличение этой составляющей в диапазоне частот тем интенсивней, чем ближе верхняя граничная частота усилителя к f_т транзистора. Поэтому и на высоких частотах изменение режима транзисторов мало влияет на величину коэффициента шума. Составляющая F'_бэ слабо зависит от частоты, F'_K на высоких частотах интенсивно растет.

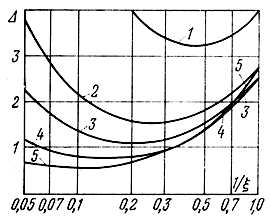
Рис. 8.7. Зависимость суммы F'_бэ, F'_к, F_Σ от ξ при различных значениях а: 0,02 (1), 0,06 (2), 0,1 (3), 0,2 (4), 0,35 (5)

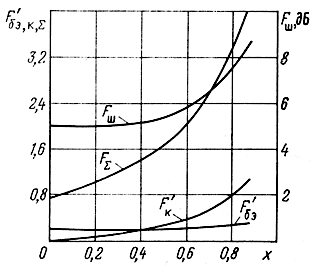
Рис. 8.8. Частотные зависимости коэффициента шума каскада УРУ на транзисторах по каскодной схеме ОЭ-ОБ

Повышенный абсолютный уровень F_ш и его рост в диапазоне частот имеют место в основном из-за влияния сопротивления и реактивностей УЭ, уменьшающих R_11к и |y_21к|. Для построения малошумящего каскада РУ можно рекомендовать выбирать частоту среза фильтров по отношению к f_т такой, чтобы

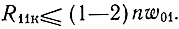
При этом потери во входной ПЛ будут сравнительно малыми и потребуется небольшое R_oc для уменьшения степени спада |y_21к|.

На рис. 8.8 показаны зависимости от x=f/f_ср составляющих F_Σ, F'_бэ, F'_к и коэффициента шума, рассчитанных для следующих значений параметров: n = 3, w₀₁ = 75 Ом, r_б = 20 Ом, R_oc = 22 Ом, r_э = 10 Ом, f_т = 1,5 ГГц, f_ср = 0,6 ГГц, β₀ = 50, L_э,б = 2 нГ, C_к1 = 0,7 пФ, С_к2 = 1,3 пФ.

В заключение следует отметить, что УРУ на современных транзисторах имеют меньший коэффициент шума по сравнению с коэффициентом шума ламповых усилителей, что подтверждают результаты испытаний многих разработанных лабораторных макетов и опытных образцов (см. табл. 10.1 и 10.2).