8.4.6. Определение оптимального коэффициента расфазировки при включении СУ в Т-образное сечение фильтра

Прежде чем приступить к анализу требуемого разноса частот среза входной и выходной ПЛ, необходимо знать n и f_Н. Число секций, как следует из (8.100), можно определить, исходя из заданного К_E410

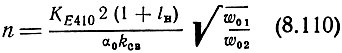
и проконтролировать при помощи условия (8.108).

Выражение для l_Н содержит неизвестную L_c, максимально допустимое значение которой ограничивается либо условием

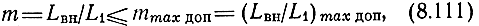
либо требованием, чтобы граничная частота СУ была не менее f_cp1

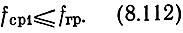
Предельная величина m_maxдоп = 1, когда вся индуктивность фильтра состоит из L_ВН. Используя (8.92а), левую часть (8.111) запишем в виде

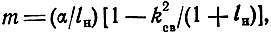
где α = L_H/L₁ = 0,5L_Hω_cp1/w₀₁, откуда

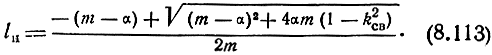
При m = m_maxдоп = 1

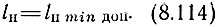
Может оказаться, что условие (8.112) является более жестким по сравнению с (8.111). В этом случае, используя (8.83), находим

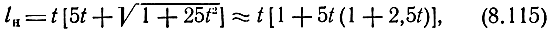
где t = 2L_Hf_гр/ρ₁₁.

При f_ср1 = f_гр l_Н становится минимально допустимым l_{п min доп}. Из значений f_н, вычисленных по (8.114) и (8.115), необходимо брать наибольшее. Более того, требуется обеспечить некоторый запас, увеличивая l_{н min доп} в q раз (q > 1). Коэффициент q целесообразно взять равным 1,5. Дальнейшее увеличение q(L_c) вызовет трудности изготовления СУ и увеличит нижнюю граничную частоту.

Таким образом,

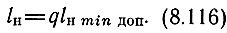
Не останавливаясь на различных причинах уменьшения коэффициента усиления каскада УРУ при стремлении частоты к нулю, рассмотрим лишь влияние симметрирующего устройства для определения нижнего предела L_c или верхнего предела l_Н. На очень низких частотах АЧХ каскада определяется величиной K_ci. При этом нагрузкой СУ можно считать лишь активную составляющую h_11б при y << 1 (8.86)

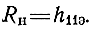
Модуль относительного коэффициента передачи по току СУ определяется из (8.77) с учетом (8.73) - (8.75)

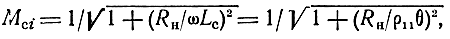
откуда, полагая M_ci = 1/√2, находим нижнюю граничную частоту ω_H = R_H/L_c. Если ω_Н задана, то нетрудно определить минимально допустимую L_c или максимально допустимое l_Н:

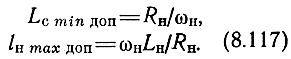
Если ω_Н должна быть как можно меньшей, то необходимо руководствоваться (8.116).

Определим величины коэффициента расфазировки при различных соотношениях между параметрами. При b_p = 1, (x₂ = b_px₁) расфазировка отсутствует:

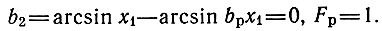
При этом АЧХ каскада (8.106) с ростом частоты увеличивается в результате роста V'_w (8.101) и при определенных ситуациях, когда спад h_21б не может скомпенсировать рост K_ci, в результате увеличения П_у (8.103). При b_p < 1 функция расфазировки (5.151) с ростом x_1,2 падает и в некоторой степени компенсирует подъем АЧХ. Дальнейшее уменьшение b_р приведет к еще большей компенсации подъема АЧХ. Первым характерным значением b_p = b_p1 является такое, при котором b₂ = π/n, F_p = 0 на x₁ = 1, т. е. на границе полосы пропускания. Если далее уменьшать коэффициент b_p, то одновременно с увеличением эффекта компенсации будет происходить сокращение полосы пропускания, поскольку F_p = 0 при x₁ < 1 (b_p < b_p1). Сокращение полосы можно допустить лишь в небольших пределах, например, на 10% (F_p = 0 при x₁ = 0,9). Такое значение b_p является минимально допустимым: b_p = b_{p min} при F_p(x₁ = 0,9) = 0. Решая уравнение nb₂ = π при x₁ = 1 и 0,9, находим

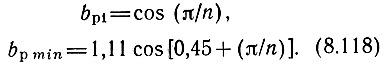
Результаты расчета b_p по (8.118) приведены в табл. 8.2. Определим коэффициент разфазировки b_p = b_p0, при ко-

тором АЧХ каскада на низких частотах (x₁ << 1) постоянна. Представляя F_p в виде (5.160) и разлагая входящие в (8.106) функции в ограниченные квадратом x₁ степенные ряды, получим выражение для АЧХ каскада на низких частотах

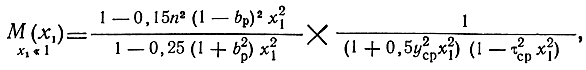
где

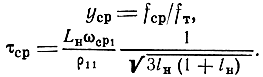
М x₁) = 1 x₁ << 1 при выполнении равенства

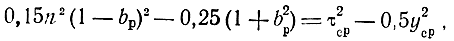
откуда

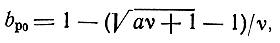
где

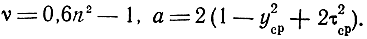
Зависимости b_p0 = f(a,n) приведены на рис. 8.17. Следует заметить, что при n > 4 b_p0 < b_p1 что говорит о том, что при b_p0 ≤ b_p ≤ b_p1 АЧХ каскада будет иметь подъем с последующим спадом до 0 на (x₁₀ < x₁ < 1), где x₁₀ > 0,9 - относительная частота, на которой F_p(b_p = b_p0) = 0.

Таблица 8.2

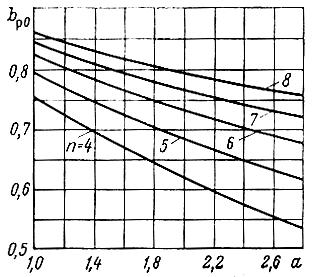
Рис. 8.17. К определению коэффициента расфазировки при взаимной компенсации различных факторов на низких частотах

Оптимальным будем называть такое, при котором М равна фиксированному значению М_ф > 1, например, М_ф = 1,1 на фиксированной относительной частоте x_1ф ≤ 1, например, x_1ф = 0,9. Очевидно, что b_p0 < b_{p opt} ≤ b_p1.

Для определения b_{p opt} воспользуемся свойством nb₂ = const для функции расфазировки F_p = const.

При фиксированных значениях x₁ и М

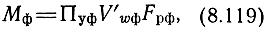
где

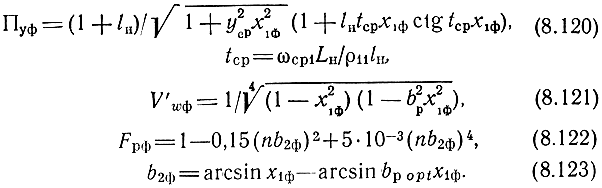
Для x_1ф = 0,9

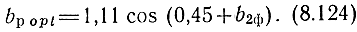
Из (8.122) и (8.119) находим

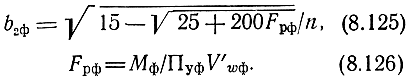
Уравнение (8.119) невозможно разрешить относительно искомого значения b_{p opt}. Однако, поскольку значения b_p, близкие к b_{p opt} (например, b_p1), известны, то, полагая, что замена b_{p opt} на b_p1 мало скажется на величине V' _wф, можно применить итерационный способ вычисления b_{p opt}.

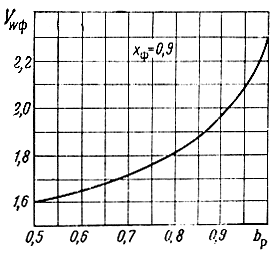
Рис. 8.18. Расчетная зависимость функции характеристических сопротивлений от коэффициента расфазировки

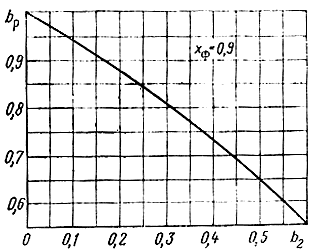
Рис. 8.19. Зависимость коэффициента расфазировки от полуразности фазовых постоянных на фиксированной частоте

Вычисляется П_уф (8.120), задается b⁽⁰⁾_{υ opt} = b_p1 в нулевом приближении; I этап - V'_wф(b⁽⁰⁾_{p opt}) (8-121); F_рф(V'_wф) (8.126); b_2ф(F_{р ф}); (8.125); b^(I)_{p opt} (b_2ф) (8.123), (8.124) - первое приближение; II - этап процесс вычисления аналогичен процессу вычисления I этапа при замене b⁽⁰⁾_{p opt} на полученное b^(I)_{p opt} в результате имеем b^(II)_{p opt} - второе приближение.

Опыт показывает, что достаточно трех этапов вычисления b_{p opt}. Для упрощения процесса расчета можно пользоваться графическими зависимостями (рис. 8.18), (8.19), вычисленными соответственно по (8.121), (8.124). Для расчета b_2ф можно также применить график на рис. 5.7.

Расчет элементов каскада при включении СУ в Т-образное сечение фильтра

Задано: параметры транзистора, w_01,02, f_cp1, К_E410, k_CB, ρ₁₁.

Рассчитываются величины: l_{н min доп} (8.114), (8.115); l_н (8.116) или (8.117); L_c = L_H/L_H, L_ВН (8.92а); L_доп = L₁ - L_BH, n (8.110); b_{p opt} (8.123-8.126) (итерационный процесс); f_cp1 = f_cp1/b_{p opt} C_1,2, L_1,2 (4.10), при этом С₂ должна быть более суммы собственной (выходной емкости транзистора, приблизительно равной С_к, и монтажной емкости С_м, добавочная емкость фильтра выходной линии С_2доб = С₂ - (С_к + С_м).